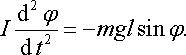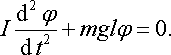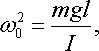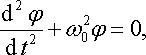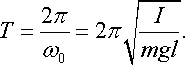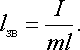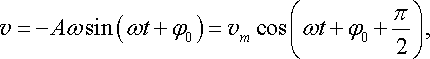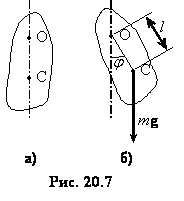
Фізичний маятник

Фізичний маятник  це масивне тверде тіло, яке може коливатися відносно осі, що не проходить через центр мас.  У стані рівноваги центр мас (центр інерції) маятника (точка С) знаходиться під точкою підвісу маятника О, на одній з ним вертикалі (рис. 20.7а). Якщо відхилити маятника на кут     від вертикалі (рис. 20.7б), то виникає момент сили тяжіння

який намагається  повернути маятник до положення рівноваги. Саме тому цей момент називають повертаючим.  В останній формулі  m  маса тіла,  l  відстань між віссю і центром мас (знак “ має той самий зміст, що і у випадку математичного маятника). Позначивши  I  момент інерції маятника відносно осі, що проходить через точку підвісу, можна записати основне рівняння динаміки обертального руху:

(20.25)

Для малих кутів цей вираз набуває вигляду:

Позначивши

(20.26)

одержимо диференціальне рівняння

розв’язок якого

(20.27)

Таким чином, при малих відхиленнях від положення рівноваги фізичний маятник здійснює гармонічні коливання з періодом

(20.28)

Співставлення формул (20.28) та (20.24) дозволяє ввести зведену довжину фізичного маятника  таку довжину математичного маятника, для якого період коливань дорівнює періоду коливань фізичного маятника:

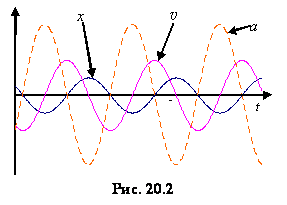
Кінематичні характеристики гармонічних коливань

Кінематичними характеристиками руху є координата, швидкість та прискорення.

Координата точки, наприклад  x, при гармонічних коливаннях змінюється з часом за законом:

(20.7)

Тут A  амплітуда коливань, тобто максимальне відхилення коливної точки від положення рівноваги A = x_max. (Звичайно, можна було б записати рівняння руху, використовуючи синус, при цьому змінилася б тільки початкова фаза).

Швидкість руху коливної точки  це похідна по часу від координати (20.7):

(20.8)

де      амплітуда (максимальне значення) швидкості. Очевидно, що швидкість випереджає по фазі зміщення на   .

Прискорення  це похідна по часу від швидкості:

(20.9)

Тут      амплітуда прискорення, а також враховано вираз (20.7). Очевидно, що зміни прискорення випереджають по фазі зміни координати на   .

Графіки залежностей від часу координати  x,  швидкості  v  та прискорення  a  показані на рис. 20.2.