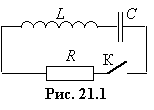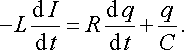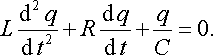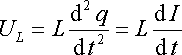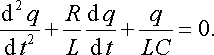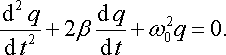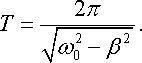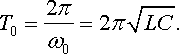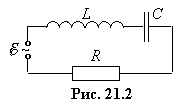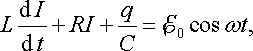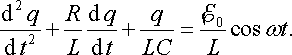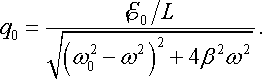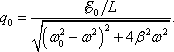32.Вільні коливання у контурі

Коливальним контуром називають коло, яке в загальному випадку складається з конденсатора ємності С, котушки з індуктивністю  L  та провідника з опором  R  (рис. 21.1).

Припустимо, що в момент часу  t = 0  конденсатор мав заряд  q₀. Якщо в цей момент замкнути ключ К, то в колі потече струм і на резисторі з’явиться напруга U_R = IR, а в котушці індуктивності     ЕРС самоіндукції . Тоді за другим правилом Кірхгофа можемо записати:

де U_C = q/C  напруга на конденсаторі. Підставивши сюди вираз для ЕРС самоіндукції  (18.13),  дістанемо

(21.1а)

Урахувавши вираз сили струму через заряд (15.1), маємо

(21.1б)

Оскільки в колі відсутні джерела сторонніх сил, то рівнянні (21.1б) можна розуміти і так, що сума напруг на окремих елементах контуру дорівнює нулеві. З цього випливає, що вираз

(21.2)

є напругою на котушці індуктивності.

Поділивши всі доданки (21.1б) на L, одержимо

Уведемо позначення:

(21.3)

та

(21.4)

Так само як  і для механічних коливань       це коефіцієнт загасання,       власна частота. Тепер останнє рівняння набуває  вигляду

(21.5)

За своєю структурою воно не відрізняється від рівняння (20.40), отже його розв’язок буде таким самим. Якщо  , то 

(21.6)

де циклічна частота визначається за формулою (20.42), а період коливань  (20.45):

(21.7)

Якщо опір (його ще називають активним опором) контуру прямує до нуля, то контур називають ідеальним і для нього

При цьому період коливань визначається за формулою Томсона

(21.8)

Вільні загасаючі коливання в контурі характеризуються таким ж параметрами як і механічні коливання:  час релаксації, логарифмічний декремент загасання, добротність. Ці величини розраховуються за формулами (20.44), (20.46), (20.48) та (20.49).

 

33. Вимушені коливання в контурі. Резонанс

Якщо коло, що складається з  резистора  R,  котушки індуктивності  L  та  конденсатора C,  приєднати до джерела змінної ЕРС, то в ньому буде текти змінний струм, амплітуда якого є сталою. Таке коло називають коливальним контуром. Джерело може приєднуватися до контуру послідовно, або ж паралельно.  У першому випадку контур називають послідовним, у другому  паралельним. У курсі загальної фізики, як правило, розглядається тільки послідовний контур.

 

Нехай у послідовному контурі (рис.21.2) ЕРС джерела змінюється у часі  за гармонічним законом

		(21.9)

За другим правилом Кірхгофа сума напруг на елементах кола дорівнює ЕРС джерела, отже

(21.10)

або ж

(21.11)

Подібно до механічних коливань, його розв’язком для усталеного режиму є функція

(21.12)

де зсув фаз    визначається формулою (20.53), а амплітуда заряду:

(21.13)

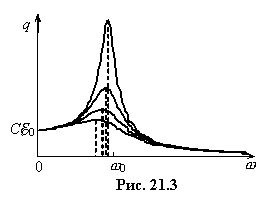
Графік цієї функції (такий самий вигляд матиме залежність напруги на конденсаторі від частоти) показаний на рис. 21.3.

Частоту, що відповідає максимуму функції , визначимо, проаналізувавши (21.13)  на екстремум. В  результаті (аналогічно до (20.54))  одержимо:

		(21.14)

Так само, як і для механічних коливань, різке зростання амплітуди коливань при наближенні частоти до   називають резонансом, а частоту      резонансною частотою.

Явище резонансу використовують для виділення сигналу певної частоти із складного сигналу. На цьому ґрунтується вся радіотехніка, включаючи телебачення і радіотелефонний зв'язок.