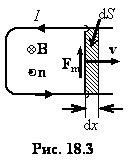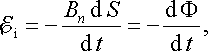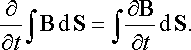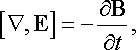- •1. Характеристики електричного струму
- •Умови існування електричного струму
- •Рівняння неперервності
- •2. Закон Ома. Опір провідників
- •Закон Ома для неоднорідної ділянки електричного кола та для замкнутого кола
- •3. Елементарні уявлення про механізм провідності металів. Закон Ома в диференціальній формі.
- •Закон Ома в диференціальній формі.
- •4. Розгалужені кола. Правила Кірхгофа
- •5. Робота і потужність струму. Закон Джоуля-Ленца
- •Робота по переносу зарядів в електричному колі
- •Потужність струму
- •Закон Джоуля-Ленца
- •6. Квазістаціонарні струми
- •8. Закон Біо-Савара
- •Магнітне поле рухомого заряду
- •Формулювання закону Біо-Савара
- •Застосування закону Біо-Савара
- •Магнітне поле прямого струму
- •Магнітне поле на осі колового струму
- •9. Основні закони магнітного поля
- •Потік вектора індукції
- •Теорема про циркуляцію вектора в (закон повного струму); вихровий (соленоїдальний) характер магнітного поля
- •Застосування теореми про циркуляцію вектора в для розрахунку індукції магнітного поля
- •10. Магнітне поле нескінченного соленоїда та тороїда (виведення формул).
- •11. Сила Ампера. Взаємодія провідників із струмом.
- •Сила Ампера
- •12. Сила і момент сили, що діють на контур в магнітному полі.(момент силы в 13 вопросе) Сила, що діє на контур із струмом у магнітному полі
- •13. Момент сили, що діє на контур із струмом у магнітному полі. Магнітний момент контуру. Момент сил, що діє на контур із струмом у магнітному полі
- •14. Робота при переміщенні контуру із струмом у магнітному полі
- •15. Намагнічування магнетиків
- •Намагніченість j
- •Струми намагнічування
- •16. Циркуляція вектора j
- •17. Вектор н (напруженість магнітного поля)
- •Магнітна сприйнятливість, магнітна проникність
- •18. Умови на межі магнетиків
- •18. Явище електромагнітної індукції. Основний закон електромагнітної індукції
- •Відкриття Фарадея
- •Основний закон електромагнітної індукції
- •20. Природа ерс індукції
- •Контур рухомий, магнітне поле незмінне
- •Контур нерухомий, магнітне поле змінюється. Вихрове електричне поле
- •Правило Ленца
- •22. Явище самоіндукції. Індуктивність
- •Індуктивність
- •Перехідні процеси в електричному колі при наявності індуктивності
- •23. Встановлення струму при вмиканні та вимиканні струму в котушці.
- •24. Енергія магнітного поля
- •25. Струм зміщення
- •26. Рівняння Максвелла
- •Система рівнянь Максвелла
- •19.3. Властивості рівнянь Максвелла
20. Природа ерс індукції
Зміна магнітного потоку можлива завдяки руху, чи деформації контуру при незмінній індукції магнітного поля, або ж завдяки змінам індукції при нерухомому контурі. Відповідно до цього повинні існувати суттєво відмінні фізичні причини виникнення ЕРС індукції.
Контур рухомий, магнітне поле незмінне
Розглянемо найпростіший випадок: замкнутий контур утворюється нерухомим П-подібним каркасом, по якому може ковзати перетинка довжини l (рис. 18.3). Припустима також, що контур знаходиться в однорідному магнітному полі, вектор індукції якого перпендикулярний площині контуру. Якщо перетинку рухати праворуч, то разом із нею впорядковано рухатимуться носії струму і на них діятиме магнітна складова сили Лоренца Fm = q[v,B]. Дія цієї сили призводить до перерозподілу зарядів у дротах контуру і в ньому з’явиться струм, напрям якого показаний стрілкою. Відповідно до напряму струму обираємо позитивну нормаль n згідно з правилом правого гвинта у напрямі до нас”. В такому разі вектори В та n напрямлені протилежно, отже магнітний потік від’ємний, що і зумовлює знак “ “ у формулі (18.1). Саме тому, вибираючи напрям нормалі, ми задаємо як знак потоку, так і знак ( полярність”) ЕРС індукції.
|
Магнітна сила, яка діє в перетиці, є сторонньою. Їй відповідає поле сторонніх сил E* = F/q = [v,B]. Циркуляція вектора E* по контуру за означенням дорівнює ЕРС
|
|
|
В даному разі стороння сила діє на довжині l перетинки, вектори v і B взаємно перпендикулярі, тому
|
|
(18.4) |
де індекс “n” біля В підкреслює той факт, вектор індукції перпендикулярний до площини, в якій рухається перетинка, і напряму вектора швидкості.
Швидкість
руху перетинки дорівнює відношенню її
переміщення dx
до
часу dt:
![]()
![]() ,
а добуток
,
а добуток
![]()
![]() це
приріст площі контуру за час dt.
Урахувавши, що вектор B
та нормаль n
до площини контуру напрямлені
протилежно, маємо
це
приріст площі контуру за час dt.
Урахувавши, що вектор B
та нормаль n
до площини контуру напрямлені
протилежно, маємо
|
|
|
що і треба було довести.
Якщо вектор В не перпендикулярний до площини контуру, то нескладно показати, що тільки його перпендикулярна складова призводить до виникнення ЕРС індукції. Можна також довести, що формула (18.1) справедлива для будь-якого контуру, що довільно рухається в постійному неоднорідному магнітному полі.
Зауважимо, що розглянутий вище принцип покладений в основу роботи індукційних генераторів електричного струму, в яких ротор з обмоткою обертається в магнітному полі.
Контур нерухомий, магнітне поле змінюється. Вихрове електричне поле
Численні експерименти беззаперечно підтвердили той факт, що у провідному замкнутому контурі індукційний струм виникає і у випадку, коли контур нерухомий, а змінюється магнітне поле, яке пронизує поверхню, натягнену на цей контур. Виникнення струму можливе тільки при наявності сторонніх сил, тому доводиться припустити, що індукційний струм виникає в результаті виникнення у дроті електричного поля.
Аналізуючи цю ситуацію, Дж. Максвел припустив, що магнітне поле, яке змінюється з часом, призводить до появи у просторі змінного електричного поля, незалежно від наявності провідного контуру. Останній лише дозволяє фіксувати появу поля за виникненням в колі електричного струму.
Таким чином, за гіпотезою Максвела магнітне поле, що змінюється з часом, породжує електричне поле. Циркуляція вектора Е цього поля по будь-якому замкнутому контуру визначається швидкістю зміни магнітного потоку, що пронизує поверхню, натягнену на контур:
|
|
(18.5) |
Символ частинної похідної в цьому виразі підкреслює той факт, що контур і натягнена на нього поверхня нерухомі і зміни в часі магнітного потоку відбуваються тільки завдяки змінам магнітного поля. Скориставшись означенням потоку для вектора В, можемо записати:
|
|
|
В цьому виразі операція взяття похідної по часу і взяття інтегралу по поверхні змінені місцями, оскільки контур нерухомий і порядок виконання цих дій не має значення. Тепер вираз (18.5) можна представити у вигляді:
|
|
(18.6) |
Визначивши ротор цього рівняння, одержимо його диференціальну форму:
|
|
(18.7) |
тобто
зміна у часі індукції В магнітного поля в даній точці простору визначає ротор вектора напруженості електричного поля Е в цій же точці простору.
Той
факт, що циркуляція вектора Е
відмінна від нуля означає, що це електричне
поле не є потенціальним. Воно, так само
як і магнітне поле, є вихровим
(інакше
![]() соленоїдальним).
Таким чином, електричне
поле може бути як потенціальним
(породжується нерухомими зарядами), так
і вихровим (породжується змінним
магнітним полем).
соленоїдальним).
Таким чином, електричне
поле може бути як потенціальним
(породжується нерухомими зарядами), так
і вихровим (породжується змінним
магнітним полем).
Із сказаного вище зрозуміло, що циркуляція вектора Е може бути зумовлена як дією магнітної сили, так і магнітним полем, що змінюється з часом. Кількісно це твердження виражається у вигляді:
|
|
(18.8) |
де
вираз у правій частині і являє собою
повну похідну по часу від магнітного
потоку:
![]() dФ/dt.
dФ/dt.
Ніякого загального принципу, який би поєднував названі причини виникнення ЕРС індукції не існує. Тому треба сприймати закон електромагнітної індукції як сумісної ефект двох різних явищ. Незважаючи на їх різну фізичну природу, результат цих явищ один виникнення ЕРС індукції, величина якої визначається швидкістю зміни магнітного потоку, що пронизує контур.