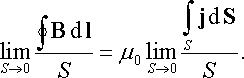9. Основні закони магнітного поля

Магнітне поле, так само як і електричне, має дві дуже важливі властивості, зв’язані з потоком вектора індукції та його циркуляцією.

Потік вектора індукції

Узагальнення експериментальних фактів дозволило дійти висновку, що потік вектора В крізь будь-яку замкнуту поверхню дорівнює нулеві. Таким чином, теорема Гауса для вектора В має вигляд:

(16.12)

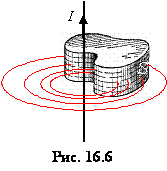
Ця теорема в постулативній формі фіксує той факт, що лінії вектора В не мають ні початку, ні кінця. Тому число ліній вектора В, що виходять з довільного об’єму, обмеженого поверхнею S, завжди дорівнює числу ліній, що входять в цей об’єм. На прикладі магнітного поля прямого струму (рис. 16.6) легко побачити справедливість сформульованого вище твердження.

Закон (16.12) виражає також ще й той факт, що в природі відсутні магнітні заряди, на яких могли б починатися, чи закінчуватися лінії вектора В.

Теорема про циркуляцію вектора в (закон повного струму); вихровий (соленоїдальний) характер магнітного поля

Подібно до циркуляції вектора  Е  можна ввести циркуляцію вектора  В:

В дослідах встановлено, що

циркуляція вектора  В  по довільному контуру  Г  дорівнює добутку сталої     на алгебраїчну суму сил струмів  І_k, що охоплюються контуром  Г:

(16.13)

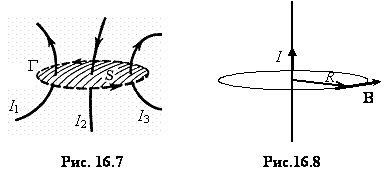
де  І_k є величинами алгебраїчними. Струм вважається позитивним, якщо його напрям зв’язаний напрямом обходу по контуру правилом правого гвинта. Струм протилежного напряму вважається від’ємним. Це правило проілюстроване на рис. 16.7: тут струми     позитивні, оскільки їх напрями зв’язані з напрямом обходу по контуру правилом правого гвинта, а струм       від’ємний.

В справедливості виразу (16.13) легко упевнитися на прикладі магнітного поля, створеного струмом I у дуже довгому (нескінченному) прямому дроті. Для цього навколо дроту побудуємо замкнутий контур у вигляді кола радіуса  R, центр якого співпадає з дротом, а площина кола перпендикулярна до осі дроту (рис. 16.8). У кожній точці цього контуру індукція магнітного поля однакова і дорівнює і визначається формулою (16.9), при цьому вектор В напрямлений по дотичній у кожній точці контуру. За таких умов циркуляція вектора В по контуру  Γ дорівнює

Оскільки магнітне поле підпорядковується принципу суперпозиції, то при наявності декількох струмів

Що треба було показати.

Якщо струм розподілений по поверхні, то його можна представити як

де інтеграл береться по довільній поверхні  S, натягнутій на контур Г. Густина струму  j  під інтегралом береться в тому місці, де розглядається площадка  dS,  причому вектор  dS  утворює з напрямом обходу по контуру правогвинтову систему. Таким чином, в загальному випадку

(16.14)

Той факт, що циркуляція вектора  В  відмінна від нуля означає, що магнітне поле не є потенціальним (на відміну від електростатичного поля). Такі поля називають вихровими, або ж соленоїдальними.

Оскільки циркуляція вектора  В  по замкнутому контуру в загальному випадку не дорівнює нулеві, для магнітного поля не можна ввести скалярний потенціал, подібний до потенціалу електростатичного поля: при кожному обході контуру він одержував би приріст на величину   .  Однак, для тих областей, де відсутні струми, вводять магнітний потенціал і ефективного його використовують.

Теорему про циркуляцію вектора В можна записати і в диференціальній формі. Для цього треба визначити ліміт відношення лівої та правої частин формули (16.14) до площі поверхні, натягнутої на контур Г за умови, що ця площа прямує до нуля:

Ліміт лівої частини дає ротор вектора  В  (rot В), а ліміт правої  прямує до густини струму в даній точці (j). Отже теорема про циркуляцію вектора  В  в диференціальний формі має вигляд:

(16.15)

Ротор вектора В може бути записаним як векторний добуток оператора набла на вектор В:

Тоді теорема про циркуляцію вектора  В  набуває вигляду:

(16.15а)

(Зауважимо, що ліва частина формули (16.15а) вимовляється як ротор вектора  В”).