23042012 Лекция 12

Действия по обработке основных событий

Наступления основных событий вызывают определённые изменения в системе, и при моделировании системы эти изменения должны быть учтены.

Прибытие заявки:

1. Планирование прихода следующей заявки;

2. Проверка состояния обслуживающего прибора. При этом:

   1. Если прибор свободен, то заявка поступает на обслуживание. Что вызывает переход прибора из свободного состояния в занятое. Планирование события окончания обслуживания.

   2. Если прибор занят, то заявка поступает в очередь, а значит, длина очереди увеличивается на единицу.

Окончание обслуживания:

1. Проверка состояния очереди. При этом:

   1. Если в очереди нет заявок, то прибор переходит из состояния занятого в свободное.

   2. Если в очереди есть заявки, то в соответствии с дисциплиной облуживания из очереди выбирается заявка на обслуживания. Длина очереди уменьшается на единицу.

2. Продвижение заявок в очереди, в результате уменьшения её длины, приводит/обязывает к планированию события окончания обслуживания.

Определение ближайшего события

Для выбранного способа коррекции значения таймера модельного времени, оно каждый раз сдвигается на момент ближайшего события. А затем модель будет обрабатывать наступившее событие с учётом его типа.

Для этого составляется список всех основных событий в порядке возрастания моментов времени, в которые они запланированы. И каждый раз модельное время будет сдвигаться на момент поступления ближайшего события. Такой список для моделирования СМО G\G\1 выглядит так:

[T_in, "прибытие заявки" ]; (присутствует всегда)

[T_out, "окончание обслуживания"]; (не всегда)

[T, "завершение моделирования"]; (всегда).

Здесь предполагается, что T_in  T_out  T.

Очевидно, что роль такого списка может быть отведена просто трем переменным T_in, T_out, T , а очередную коррекцию модельного времени выполнить согласно равенству:

.

В списке событий событие окончания обслуживания присутствует невсегда, соответственно значение времени T_out имеет место, только если оно запланированное.

Чтобы не отказаться от равенства для определения модельного времени t_M (если прибор занят обслуживанием), вводится в список событий псевдо-событие "окончание обслуживания" с моментом наступления , например, . Очевидно, что такое псевдо-событие никогда не наступит (скорее наступит событие "окончание моделирования").

Изложенные здесь положения обобщены в блок-схеме алгоритма имитационной модели, которая представлена на рис.4.3.

Приведем необходимые пояснения по отдельным блокам.

Блок 1. Ввод исходных данных, в качестве которых рассматриваются функции распределения A(t), B(t) и время моделирования Т.

Блок 2. В этом блоке обнуляются все переменные и массивы, которые предназначены для следующих целей:

F — задает состояние приборы: F = 0, если прибор свободен и F = 1, если занят.

N_in — счетчик входов (определяет число вошедших в модель заявок).

N_out — счетчик выходов.

N_q — текущая длина очереди.

Nq_max — максимальная длина очереди.

T_in — момент прихода заявки.

T_out — момент окончания обслуживания.

Stв, St, Stu — переменные для накопления суммарных значений времен обслуживания, ожидания и пребывания соответственно.

Mtq[...] — массив, который фиксирует моменты становления заявок в очередь.

t_м — модельное время.

N0 — счетчик заявок, которые проходят очередь без ожидания.

Блок 3. Равенство означает розыгрыш случайной величины, распределенной по закону A(t), где A^-1(x) — обратная функция.

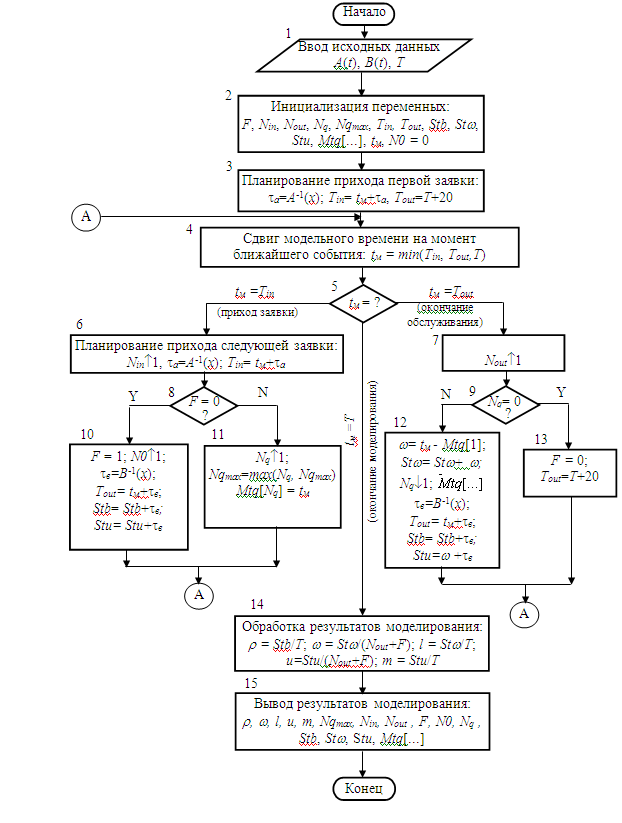
Рис. 4.3. Блок-схема логики работы имитационной модели.