25. Принципы построения пкн на предельных многоступенчатых омических сетках. Примеры пкн для двоичных кодов.

Многоузловые предельные сетки сопротивления получают путем рзаделения одноузловой матрицы на n групп по числу разрядов преобразуемого код N. При этом предполагается, что исходное число разрядов одноузловой резисторной матриц равно бесконечности. Каждая группа состоит из S резисторов и представляет собой одноузловую резисторную матрицу. Одноузловые S-резисторные матрицы связывают сопротивления связи (Rсв), величина которых рассчитывается таким образом, чтобы S-разрядные матрицы по используемым в них номиналам резисторов оказались идентичными. После выделения n S-разрядных резисторный матриц, оставшуюся часть исходно одноузловой матрицы заменяют корректирующим сопротивлением: R_корр = R_св + R_{вых ∞}. Анализ таким матриц показывает, что R_корр = R_{младшего разряда}.

ПКН на предельной многоузловой матрицы для двоичного кода.

R _св = (R / 2)(2^S - 1), R_вых = R / 2, S = ] log₂ρ [.

ρ = 2, S = 1. Пусть n = 4:

R_корр = R_св + R_{вых ∞ =} R/2 + R/2 = R.

U₀ = m_u N; m_u = U₀/N_max + 1 = U₀ / 2ⁿ = U₀ / ρⁿ.

В результате: сопротивление выхода не зависит от числа разрядов, все используемые проводимости (сопротивления) одинаковы при любом числе разрядов.

39. Двоично-десятичные пкн на предельных многоступенчатых сетках сопротивлений.

Д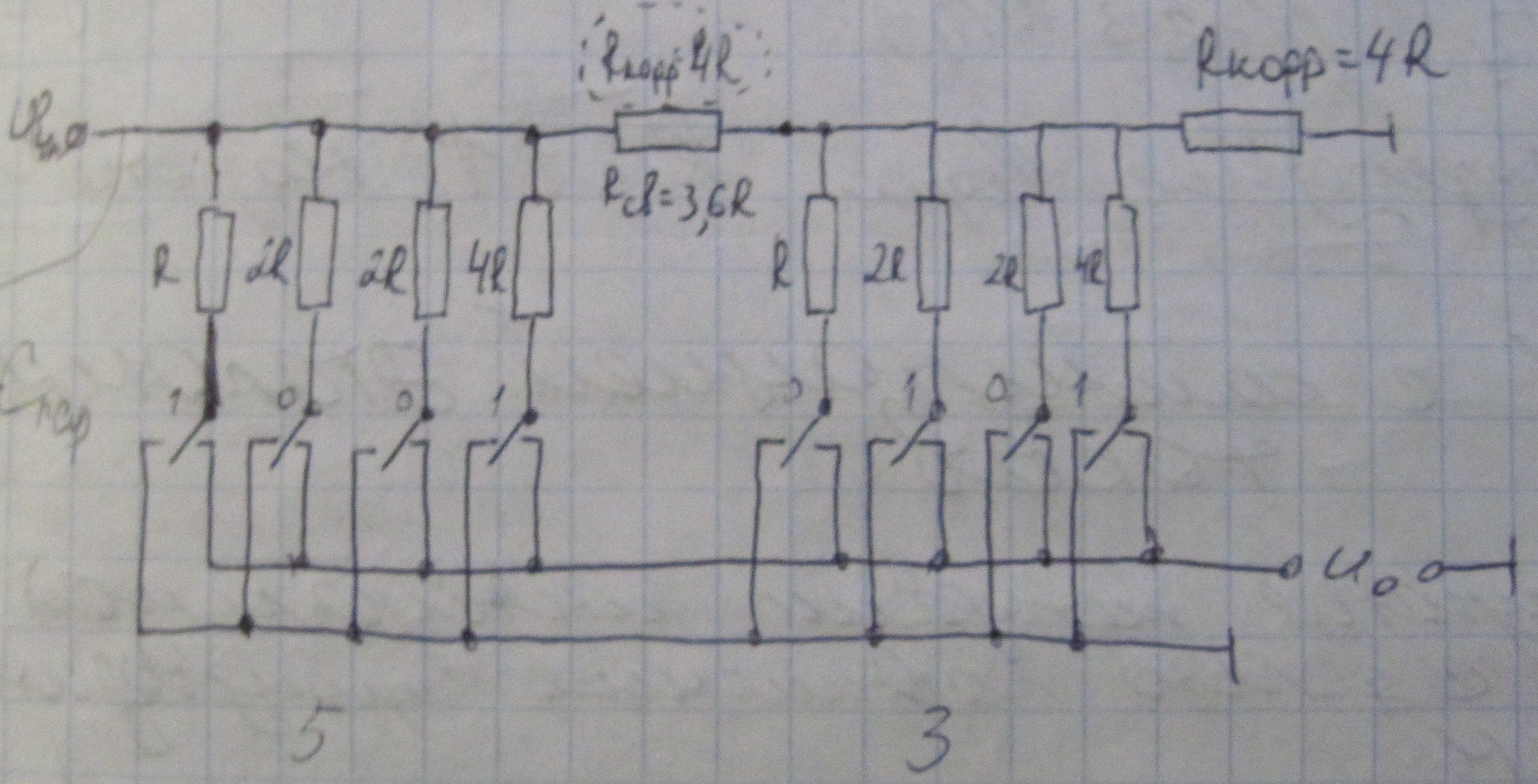 ля матрицы сопротивления в случае двоично-десятичного кода нельзя использовать соотношения, которые верны для двоичного кода (вычисление R_св). При кодировании десятичного кода будем использовать веса разрядов 4-2-2-1.

ρ = 10, S = ] log₂ρ [ , n = 2, R_j = (R*q_max) / q_j.

Для одноразрядной матрицы:

28. Аналого-цифровое преобразование. Классические алгоритмы преобразования.

Аналого-цифровые преобразователи (АЦП) выполняют квантование по уровню в процессе преобразования аналоговой величины в цифровую, т.е. сопровождаются измерительным процессом. Любой измерительный процесс предполагает определенный порядок действий для получения результатов измерения. Поэтому все АЦП работают в соответствии с тем или иным алгоритмом преобразования, который представляет собой процесс сопоставления аналоговой величины с набором ее эталонных значений с целью получения цифрового эквивалента.

Примем: q – основание системы счисления, n – разрядность выходного кода, N – результат измерения, τ – время выполнения одного такта преобразования.

К классическим алгоритмам АЦП относятся:

1. Алгоритм последовательного счета: число компараторов – 1, число разных эталонов – qⁿ-1, ассортимент эталонов – 1, число тактов алгоритма – N. Время сравнения T_пр = τ N = τ (qⁿ-1). Суть: начиная с минимального значения проверяются на равенство подряд все возможные значения выходного кода.

2. Алгоритм поразрядного кодирования: число компараторов – 1, число разных эталонов – n, ассортимент эталонов – n, число тактов алгоритма – n. Время сравнения T_пр = τ n постоянно и не зависит от выходной величины. За один такт алгоритма определяется значение одного разряда выходного кода.

3. Алгоритм считывания: число компараторов – qⁿ-1, число разных эталонов – qⁿ-1, ассортимент эталонов – qⁿ-1, число тактов алгоритма – 1. Время сравнения T_{пр =} τ. Суть: работают несколько компараторов, настроенных на сравнения входной величины с различными возможными значениями. Расстановка эталонов на оси возможных значений: Δ = 1 / qⁿ. При n = 2, q = 2 на выходе компараторов – двоичные непозиционные кода. Избыточность кодов определяет их помехозащищенность: есть разрешенные и запрещенные комбинации. Таблица – соответствие выходного кода, снятого с компараторов результирующему выходному коду:

Интервал, где находится измеряемая величина	к1	к2	к3	а1	а2
	Коды выходов компараторов
0, ¼	0	0	0	0	0
¼, ½	1	0	0	0	1
½, ¾	1	1	0	1	0
¾, 1	1	1	1	1	1