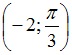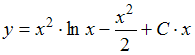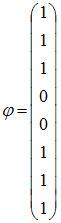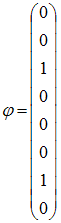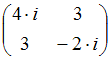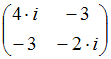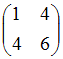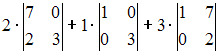На
отрезке ![]() задано
дифференциальное уравнение
задано
дифференциальное уравнение ![]() .
Значение производной второго порядка
в точке
.
Значение производной второго порядка
в точке ![]() может
быть заменено выражением …
может
быть заменено выражением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение
дифференцируемой функции ![]() в
точке
в
точке ![]() можно
приближенно найти как …
можно
приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция ![]() представлена
таблицей:
представлена
таблицей:
 Тогда
в интерполяционном полиноме Лагранжа
2-ой степени с узлами
Тогда
в интерполяционном полиноме Лагранжа
2-ой степени с узлами ![]() ,
составленном по этой таблице для
приближенного вычисления
,
составленном по этой таблице для
приближенного вычисления ![]() при
условии
при
условии ![]() значение
значение ![]() не
может быть равно …
не
может быть равно …
|
|
|
8 |
|
|
|
23 |
|
|
|
12 |
|
|
|
20 |
Уравнение ![]() решается
методом касательных (Ньютона). Корень
принадлежит интервалу
решается
методом касательных (Ньютона). Корень
принадлежит интервалу ![]() .
Тогда первое приближение
.
Тогда первое приближение ![]() к
точному корню
к
точному корню ![]() будет
вычисляться по формуле …
будет
вычисляться по формуле …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центр
окружности ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормальное
уравнение плоскости ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центр
сферы ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кривая
в полярной системе координат задана
уравнением ![]() .
Тогда ее уравнение в прямоугольной
системе координат имеет вид …
.
Тогда ее уравнение в прямоугольной
системе координат имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное
решение дифференциального уравнения ![]() ,
удовлетворяющее условию
,
удовлетворяющее условию ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После
понижения порядка дифференциальное
уравнение ![]() приводится
к виду …
приводится
к виду …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если подкасательная в любой точке кривой равна удвоенной абсциссе точки касания, то уравнение этой кривой будет иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий
вид частного решения ![]() линейного
неоднородного дифференциального
уравнения второго порядка
линейного
неоднородного дифференциального
уравнения второго порядка ![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По
выборке объема ![]() найдена
выборочная дисперсия
найдена
выборочная дисперсия ![]() .
Тогда исправленное среднее квадратическое
отклонение равно …
.
Тогда исправленное среднее квадратическое
отклонение равно …
|
|
|
2,0 |
|
|
|
4,0 |
|
|
|
3,24 |
|
|
|
1,8 |
Из
генеральной совокупности извлечена
выборка объема ![]() :
:
 Тогда
значение
Тогда
значение ![]() равно
…
равно
…
|
|
|
34 |
|
|
|
81 |
|
|
|
47 |
|
|
|
33 |
Основная
гипотеза имеет вид ![]() .
Тогда конкурирующей может являться
гипотеза …
.
Тогда конкурирующей может являться
гипотеза …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дан
доверительный интервал ![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
|
|
|
1,12 |
|
|
|
0,01 |
|
|
|
2,24 |
|
|
|
13,56 |
Сумма
комплексных чисел ![]() и
и ![]() равна
…
равна
…
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
Все
точки ![]() комплексной
плоскости, принадлежащие множеству
комплексной
плоскости, принадлежащие множеству ![]() ,
изображенному на рисунке:
,
изображенному на рисунке:
 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель
системы 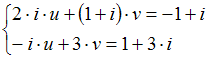 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель системы равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Площадь
треугольника с вершинами в
точках ![]() ,
, ![]() и
и ![]() равна …
равна …
|
|
|
7,5 |
|
|
|
15 |
|
|
|
5 |
|
|
|
2,5 |
Векторы ![]() ,
, ![]() и
и ![]() компланарны,
если параметр
компланарны,
если параметр ![]() равен
…
равен
…
|
|
|
– 3 |
|
|
|
3 |
|
|
|
6 |
|
|
|
|
Даны
векторы ![]() и
и ![]() ,
угол между которыми равен
,
угол между которыми равен ![]() .
Тогда проекция вектора
.
Тогда проекция вектора ![]() на
вектор
равна …
на
вектор
равна …
|
|
|
3 |
|
|
|
– 2 |
|
|
|
6 |
|
|
|
|
Модуль
градиента скалярного поля ![]() в
точке
в
точке ![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
4 |
Дано
двухмерное векторное пространства с
базисом ![]() .
Если вектор
.
Если вектор ![]() ,
то вектор
,
то вектор ![]() может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Фундаментальное решение может быть вычислено для системы вида …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрице  соответствует
квадратичная форма
соответствует
квадратичная форма ![]() ,
равная …
,
равная …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель ![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Множество
первообразных функции  имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
определенного интеграла  справедливо
неравенство …
справедливо
неравенство …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Максимум
функции  равен
…
равен
…
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
Функция  непрерывна
на отрезке …
непрерывна
на отрезке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отображение,
действующее из отрезка ![]() на
действительную числовую ось и имеющее
обратное отображение, может быть задано
функцией …
на
действительную числовую ось и имеющее
обратное отображение, может быть задано
функцией …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны
два множества: ![]() и
и ![]() .
Тогда количество целых значений
.
Тогда количество целых значений ![]() ,
принадлежащих объединению множеств
,
принадлежащих объединению множеств ![]() и
и ![]() ,
равно …
,
равно …
|
8
| |
Расстояние
между точками ![]() и
и ![]() в
метрике
в
метрике ![]() ,
где
,
где ![]() и
и ![]() ,
равно …
,
равно …
|
|
|
10 |
|
|
|
1 |
|
|
|
|
|
|
|
– 1 |
Мера
плоского множества, изображенного на
рисунке,
 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
дискретной случайной величины ![]() :
:
 функция
распределения вероятностей имеет
вид:
функция
распределения вероятностей имеет
вид:
 Тогда
значение параметра
Тогда
значение параметра ![]() может
быть равно …
может
быть равно …
|
|
|
0,7 |
|
|
|
1 |
|
|
|
0,85 |
|
|
|
0,6 |
Банк выдает 40% всех кредитов юридическим лицам, а 60% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,1; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило физическое лицо, равна …
|
|
|
|
|
|
|
|
|
|
|
0,07 |
|
|
|
0,05 |
Непрерывная
случайная величина ![]() задана
функцией распределения вероятностей:
задана
функцией распределения вероятностей:
 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Высказывание
«![]() »
означает, что …
»
означает, что …
|
|
|
« – любое число» |
|
|
|
«
принадлежит
интервалу |
|
|
|
«
принадлежит
промежутку |
|
|
|
« не существует» |
На 10 карточках написаны буквы так, что из этих карточек можно получить слово ИСЧИСЛЕНИЕ. Сколько существует различных 10-буквенных слов, которые можно образовать с помощью этих десяти карточек?
|
151200
| |
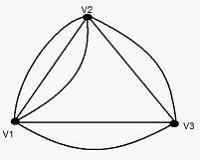
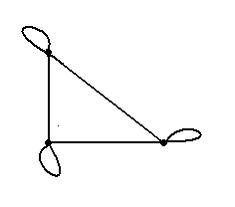
Матрица
смежности графа, изображенного на
рисунке
 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из
трех предикатов отношений между
множествами ![]() и
и ![]() :
:
![]() ,
,
![]() ,
,
![]() ,
изображенным
на рисунке
,
изображенным
на рисунке
 является …
является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
все три |
Промежуток
убывания функции 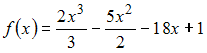 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
функции  точка
точка ![]() является
точкой …
является
точкой …
|
|
|
разрыва первого рода |
|
|
|
разрыва второго рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Функция ![]() задана
и непрерывна на всей числовой
прямой,
задана
и непрерывна на всей числовой
прямой, ![]() и
и ![]() –
действительные числа. Тогда верно
утверждение …
–
действительные числа. Тогда верно
утверждение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Множество
первообразных функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скалярное произведение векторов и равно 5, угол между векторами равен , норма вектора равна 2. Тогда норма вектора равна …
|
|
|
5 |
|
|
|
|
|
|
|
2,5 |
|
|
|
3 |
Модуль
градиента скалярного поля ![]() в
точке
в
точке ![]()
![]() равен
7 при
равном
…
равен
7 при
равном
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точки ![]() ,
, ![]() ,
, ![]() и
и ![]() лежат
в одной плоскости, если параметр
лежат
в одной плоскости, если параметр ![]() равен
…
равен
…
|
|
|
2 |
|
|
|
0 |
|
|
|
1 |
|
|
|
– 2 |
Даны
два вектора: ![]() и
и ![]() ,
где
,
где ![]() ,
, ![]() ,
угол между векторами
,
угол между векторами ![]() и
и ![]() равен
равен ![]() .
Тогда площадь треугольника, построенного
на векторах
и
будет
равна …
.
Тогда площадь треугольника, построенного
на векторах
и
будет
равна …
|
|
|
2,5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
Уравнением
кривой второго порядка ![]() на
плоскости определяется …
на
плоскости определяется …
|
|
|
эллипс |
|
|
|
гипербола |
|
|
|
парабола |
|
|
|
пара пересекающихся прямых |
В
полярной системе координат дана точка  .
Тогда расстояние от нее до полярной оси
равно …
.
Тогда расстояние от нее до полярной оси
равно …
|
|
|
4 |
|
|
|
8 |
|
|
|
16 |
|
|
|
2 |
Даны
уравнения поверхностей второго
порядка:
А)  B)
B) 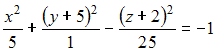 C)
C)  D)
D)  Тогда
двуполостный гиперболоид задается
уравнением …
Тогда
двуполостный гиперболоид задается
уравнением …
|
|
|
B |
|
|
|
C |
|
|
|
A |
|
|
|
D |
Геометрическое
место точек, удаленных от плоскости ![]() на
2 единицы, может иметь вид …
на
2 единицы, может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методом
Эйлера решается задача Коши ![]() ,
, ![]() с
шагом
с
шагом ![]() .
Тогда значение искомой функции
.
Тогда значение искомой функции ![]() в
точке
в
точке ![]() будет
равно …
будет
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На
рисунке изображен график функции ![]() :
:
 Тогда
корень уравнения
Тогда
корень уравнения ![]() отделен
на отрезке …
отделен
на отрезке …
|
|
|
[–1; 1] |
|
|
|
[2; 4] |
|
|
|
[–4; 6] |
|
|
|
[–3; –1] |
Интерполяционный
многочлен Лагранжа второй степени ![]() может
быть составлен по таблице значений
функции
может
быть составлен по таблице значений
функции ![]() вида
…
вида
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение
дифференциала функции  в
точке
в
точке ![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Дискретная
случайная величина
задана
законом распределения вероятностей:
![]() Тогда
вероятность
Тогда
вероятность ![]() равна
…
равна
…
|
|
|
0,5 |
|
|
|
0,8 |
|
|
|
0,7 |
|
|
|
0,1 |
Непрерывная
случайная величина
задана
плотностью распределения вероятностей:
 Тогда
ее математическое ожидание равно …
Тогда
ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
Банк выдает 35% всех кредитов юридическим лицам, а 65% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,1. Тогда вероятность непогашения в срок очередного кредита равна …
|
|
|
0,1175 |
|
|
|
0,125 |
|
|
|
0,8825 |
|
|
|
0,1275 |
Если ![]() и
и ![]() ,
то производная функции
,
то производная функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
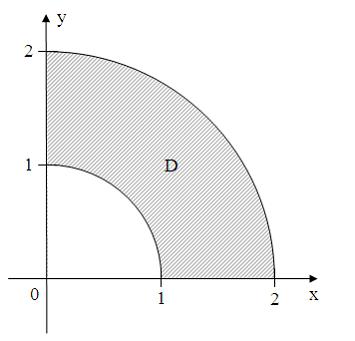 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система  решается
методом Крамера по формулам
решается
методом Крамера по формулам ![]() ,
, ![]() .
Тогда вспомогательный определитель
.
Тогда вспомогательный определитель ![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное
от деления ![]() двух
комплексных чисел
двух
комплексных чисел  и
и  равно
…
равно
…
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Даны
два множества: ![]() и
и ![]() .
Тогда количество целых значений
,
принадлежащих пересечению множеств
и
,
равно …
.
Тогда количество целых значений
,
принадлежащих пересечению множеств
и
,
равно …
|
4 |
Образом
отрезка  при
отображении
при
отображении ![]() является
отрезок …
является
отрезок …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция ![]() ,
где
,
где ![]() –
действительные числа, …
–
действительные числа, …
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме треугольника |
Плоская
мера отрезка [0; 1], лежащего на оси ![]() в
плоскости
в
плоскости ![]() равна
…
равна
…
|
|
|
0 |
|
|
|
1 |
|
|
|
бесконечности |
|
|
|
несчетна |
Симметричным бинарным отношением является отношение …
|
|
|
«слова x и y содержат одинаковое число букв» |
|
|
|
«студент x старше студента y» |
|
|
|
«x является отцом y» |
|
|
|
«город x расположен южнее города y» |
Симметричным бинарным отношением является отношение …
|
|
|
«слова x и y содержат одинаковое число букв» |
|
|
|
«студент x старше студента y» |
|
|
|
«x является отцом y» |
|
|
|
«город x расположен южнее города y» |
Для
функции ![]() ,
заданной таблицей,
,
заданной таблицей,
 СДНФ
имеет вид …
СДНФ
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
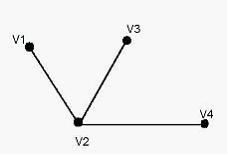
Для
графа, изображенного на рисунке,
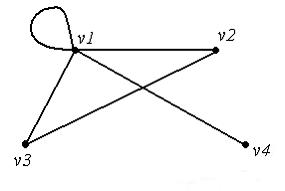 степень
вершины
степень
вершины ![]() равна …
равна …
|
|
|
5 |
|
|
|
4 |
|
|
|
3 |
|
|
|
1 |
По выборке объема найдена выборочная дисперсия . Тогда исправленное среднее квадратическое отклонение равно …
|
|
|
2,0 |
|
|
|
4,0 |
|
|
|
3,24 |
|
|
|
1,8 |
Дан
доверительный интервал ![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при увеличении объема
выборки этот доверительный интервал
может принять вид …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при увеличении объема
выборки этот доверительный интервал
может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Статистическое
распределение выборки имеет вид
 Тогда
объем выборки равен …
Тогда
объем выборки равен …
|
|
|
67 |
|
|
|
40 |
|
|
|
5 |
|
|
|
107 |
Соотношением
вида ![]() можно
определить …
можно
определить …
|
|
|
левостороннюю критическую область |
|
|
|
правостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
Корень
уравнения  равен
…
равен
…
|
|
|
– 1 |
|
|
|
1 |
|
|
|
– 5 |
|
|
|
3 |
Решение
системы линейных уравнений  методом
Крамера может иметь вид …
методом
Крамера может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрице соответствует квадратичная форма , равная …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Совокупность
векторов ![]() ,
, ![]() ,
, ![]() не
может являться базисом
трехмерного линейного пространства,
если
не
может являться базисом
трехмерного линейного пространства,
если ![]() равно …
равно …
|
|
|
2 |
|
|
|
4 |
|
|
|
1 |
|
|
|
3 |
Общее
решение линейного неоднородного
дифференциального уравнения второго
порядка ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее
решение дифференциального уравнения ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее
решение дифференциального
уравнения ![]() при
при ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение
задачи Коши ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 6 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретная
случайная величина X задана
законом распределения вероятностей:
 Тогда
ее математическое ожидание равно …
Тогда
ее математическое ожидание равно …
|
|
|
4,6 |
|
|
|
5,0 |
|
|
|
3,0 |
|
|
|
4,9 |
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Для дискретной случайной величины : функция распределения вероятностей имеет вид: Тогда значение параметра может быть равно …
|
|
|
0,7 |
|
|
|
1 |
|
|
|
0,85 |
|
|
|
0,6 |
Из
генеральной совокупности извлечена
выборка объема ![]() ,
гистограмма относительных частот
которой имеет вид
,
гистограмма относительных частот
которой имеет вид
 Тогда
значение a равно
…
Тогда
значение a равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Левосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дан
доверительный интервал ![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
|
|
|
36,62 |
|
|
|
36,52 |
|
|
|
9,12 |
|
|
|
73,24 |
Проведено
пять измерений (без систематических
ошибок) некоторой случайной величины
(в мм): 2,1; 2,3; ![]() ;
2,7; 2,9. Если несмещенная оценка
математического ожидания равна 2,48,
то
равно
…
;
2,7; 2,9. Если несмещенная оценка
математического ожидания равна 2,48,
то
равно
…
|
|
|
2,4 |
|
|
|
2,5 |
|
|
|
2,6 |
|
|
|
2,48 |
Дифференциальное
уравнение ![]() будет
уравнением с разделяющимися переменными
при значении
,
равном …
будет
уравнением с разделяющимися переменными
при значении
,
равном …
|
|
|
2 |
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Частное
решение дифференциального уравнения ![]() может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий вид частного решения линейного неоднородного дифференциального уравнения второго порядка будет выглядеть как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение задачи Коши , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определенный
интеграл 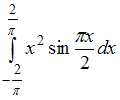 равен
…
равен
…
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
Максимум функции равен …
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
Множество
первообразных функции  имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мНа
отрезке
задано
дифференциальное уравнение ![]() .
Значение производной в точке
.
Значение производной в точке ![]() может
быть заменено выражением …
может
быть заменено выражением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция
представлена
таблицей
 Тогда
значение
Тогда
значение ![]() ,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
6 |
Значение
определенного интеграла  по
формуле трапеций можно приближенно
найти как …
по
формуле трапеций можно приближенно
найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На
рисунке изображены графики
функций
и ![]() :
:
 Тогда
корень уравнения
Тогда
корень уравнения ![]() отделен
на отрезке …
отделен
на отрезке …
|
|
|
[5; 6] |
|
|
|
[–4; 6] |
|
|
|
[–4; 0] |
|
|
|
[4; 5] |
Отрицательно определенная квадратичная форма может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель  равен
…
равен
…
|
|
|
– 22 |
|
|
|
2 |
|
|
|
|
|
|
|
22 |
Вектор ![]() является
линейной комбинацией векторов
является
линейной комбинацией векторов ![]() и
и ![]() ,
если
,
если ![]() ,
то
равно
…
,
то
равно
…
|
|
|
3 |
|
|
|
2 |
|
|
|
– 2 |
|
|
|
– 3 |
Фундаментальное решение может быть вычислено для системы вида …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дано
множество ![]() и
бинарное отношение
и
бинарное отношение ![]() ,
и
,
и ![]() делит
делит ![]() без
остатка. Тогда количество элементов
предикаты P равно
…
без
остатка. Тогда количество элементов
предикаты P равно
…
|
|
|
7 |
|
|
|
64 |
|
|
|
8 |
|
|
|
12 |
Нулевой
набор у формулы ![]() получается
при следующих значениях переменных …
получается
при следующих значениях переменных …
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
, |
Сколько чисел меньших, чем миллион можно написать с помощью цифр 3 и 7?
|
126
| |
Объем
пирамиды с вершинами в точках ![]() ,
, ![]() ,
, ![]() и
и ![]() равен …
равен …
|
|
|
18 |
|
|
|
108 |
|
|
|
54 |
|
|
|
36 |
Даны
два вектора: ![]() и
и ![]() ,
где
,
где ![]() ,
, ![]() ,
угол между векторами
и
равен
.
Тогда модуль векторного произведения
векторов
и
будет
равен …
,
угол между векторами
и
равен
.
Тогда модуль векторного произведения
векторов
и
будет
равен …
|
|
|
21 |
|
|
|
|
|
|
|
42 |
|
|
|
|
Норма
вектора ![]() в
евклидовом пространстве со стандартным
скалярным произведением равна …
в
евклидовом пространстве со стандартным
скалярным произведением равна …
|
|
|
6 |
|
|
|
– 2 |
|
|
|
36 |
|
|
|
10 |
Модуль
градиента скалярного поля ![]() в
точке
в
точке ![]() равен
5 при
равном
…
равен
5 при
равном
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение
директрисы параболы, проходящей через
точки ![]() ,
, ![]() и
симметричной относительно оси
,
имеет вид …
и
симметричной относительно оси
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение
плоскости, проходящей через точки ![]() ,
, ![]() и
и ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полярные
координаты точки, симметричной
точке  относительно
полюса, равны …
относительно
полюса, равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расстояние
между точками ![]() и
в
метрике
,
где
и
,
равно …
и
в
метрике
,
где
и
,
равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
Даны
три множества: ![]() ,
, ![]() и
и ![]() .
Тогда число элементов множества
.
Тогда число элементов множества ![]() равно …
равно …
|
5 | |
Частное ![]() комплексных
чисел
комплексных
чисел ![]() и
и ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение
производной функции 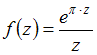 в
точке
в
точке ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если ![]() и
и ![]() являются
решением системы линейных уравнений
являются
решением системы линейных уравнений 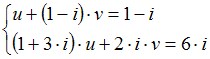 ,
то
,
то ![]() равно
…
равно
…
|
|
|
2 |
|
|
|
|
|
|
|
32 |
|
|
|
0 |
Бинарному
отношению кратности элементов, заданному
на множестве чисел ![]() соответствует
орграф…
соответствует
орграф…
|
|
|
|
На 10 карточках написаны буквы так, что из этих карточек можно получить слово ИСЧИСЛЕНИЕ. Сколько существует различных 10-буквенных слов, которые можно образовать с помощью этих десяти карточек?
|
151200
| |
Из
трех логических выражений:
![]()
![]()
![]() эквивалентными
являются …
эквивалентными
являются …
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
все функции |
Точка ![]() является
точкой разрыва функции …
является
точкой разрыва функции …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее
значение функции ![]() на
отрезке
на
отрезке  равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Множество
первообразных функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение
дифференцируемой функции
в
точке ![]() можно
приближенно найти как …
можно
приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция представлена таблицей: Тогда в интерполяционном полиноме Лагранжа 2-ой степени с узлами , составленном по этой таблице для приближенного вычисления при условии значение не может быть равно …
|
|
|
8 |
|
|
|
23 |
|
|
|
12 |
|
|
|
20 |
Если
и ![]() ,
то мнимая часть производной этой
функции
,
то мнимая часть производной этой
функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если и являются решением системы линейных уравнений , то равно …
|
|
|
2 |
|
|
|
|
|
|
|
32 |
|
|
|
0 |
Частное от деления двух комплексных чисел и равно …
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Двусторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Двусторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна …
|
|
|
0,13 |
|
|
|
0,065 |
|
|
|
3,9 |
|
|
|
0,7 |
Из
генеральной совокупности извлечена
выборка объема ![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
 Тогда
относительная частота варианты
Тогда
относительная частота варианты ![]() в
выборке равна …
в
выборке равна …
|
|
|
0,05 |
|
|
|
0,06 |
|
|
|
0,25 |
|
|
|
0,20 |
Объем
параллелепипеда, построенного на
векторах ![]() ,
, ![]() и
и ![]() ,
равен …
,
равен …
|
|
|
16 |
|
|
|
|
|
|
|
8 |
|
|
|
4 |
Норма вектора в евклидовом пространстве со стандартным скалярным произведением равна …
|
|
|
6 |
|
|
|
– 2 |
|
|
|
36 |
|
|
|
10 |
Модуль градиента скалярного поля в точке равен 5 при равном …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Площадь
параллелограмма, построенного на
векторах ![]() и
и ![]() ,
равна …
,
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Канонический
вид квадратичной формы ![]() может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны
матрица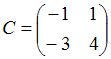 перехода
от старого базиса к новому и вектор
перехода
от старого базиса к новому и вектор ![]() с
координатами в новом базисе. Тогда
координаты вектора
с
координатами в новом базисе. Тогда
координаты вектора ![]() в
старом базисе имеют вид …
в
старом базисе имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расстояние между точками и в метрике , где и , равно …
|
|
|
10 |
|
|
|
1 |
|
|
|
|
|
|
|
– 1 |
Пусть
задано отображение ![]() .
Тогда
.
Тогда ![]() представляет
собой …
представляет
собой …
|
|
|
единичную окружность |
|
|
|
отрезок |
|
|
|
квадрат |
|
|
|
гиперболу |
Мера
плоского множества ![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
Даны
три множества: ![]() ,
, ![]() и
и ![]() .
Тогда число элементов множества
.
Тогда число элементов множества ![]() равно
…
равно
…
|
3 |
Точка ![]() задана
в прямоугольной системе координат.
Тогда ее полярные координаты равны …
задана
в прямоугольной системе координат.
Тогда ее полярные координаты равны …
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
, |
Нормальное уравнение плоскости имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношение
 в
прямоугольной декартовой системе
координат задает …
в
прямоугольной декартовой системе
координат задает …
|
|
|
параболу |
|
|
|
гиперболу |
|
|
|
эллипс |
|
|
|
окружность |
Вершина
параболоида ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное решение дифференциального уравнения может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциальное уравнение будет уравнением с разделяющимися переменными при значении , равном …
|
|
|
2 |
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно трем. Тогда вероятность того, что за два часа поступит пять заявок можно вычислить как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Непрерывная
случайная величина
задана
плотностью распределения вероятностей 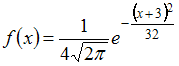 .
Тогда математическое ожидание a и
среднее квадратическое отклонение
.
Тогда математическое ожидание a и
среднее квадратическое отклонение ![]() этой
случайной величины равны …
этой
случайной величины равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение
производной функции ![]() в
точке
в
точке ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке: удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Произведение комплексных чисел и равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение определенного интеграла по формуле парабол (Симпсона) можно приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительный
корень уравнения ![]() принадлежит
интервалу …
принадлежит
интервалу …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция
представлена
таблицей
 Тогда
значение
Тогда
значение ![]() ,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
– 6 |
Соотношением вида можно определить …
|
|
|
левостороннюю критическую область |
|
|
|
правостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
|
|
|
36,62 |
|
|
|
36,52 |
|
|
|
9,12 |
|
|
|
73,24 |
Из
генеральной совокупности извлечена
выборка объема
:
 Тогда
относительная частота варианты
Тогда
относительная частота варианты ![]() равна
…
равна
…
|
|
|
0,25 |
|
|
|
0,75 |
|
|
|
0,24 |
|
|
|
0,04 |
Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна …
|
|
|
6,38 |
|
|
|
6,42 |
|
|
|
6,1 |
|
|
|
6,4 |
Пусть
некоторое бинарное отношение задается
орграфом, изображенным на рисунке:
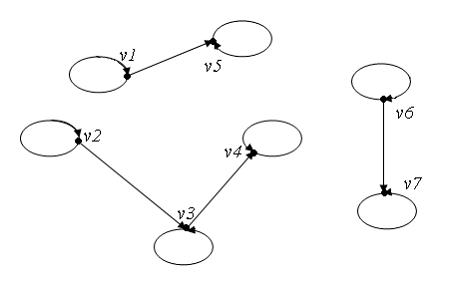 Тогда
это отношение является …
Тогда
это отношение является …
|
|
|
рефлексивным |
|
|
|
симметричным |
|
|
|
антисимметричным |
|
|
|
транзитивным |
Формулой,
равносильной формуле ![]() , является …
, является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мМатрица
инцидентности графа, изображенного на
рисунке
 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее
решение дифференциального уравнения  имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное
решение
линейного
неоднородного дифференциального
уравнения второго порядка ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее
решение дифференциального уравнения ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретная
случайная величина
задана
функцией распределения вероятностей
 Тогда
вероятность
Тогда
вероятность ![]() равна
…
равна
…
|
|
|
0,54 |
|
|
|
0,38 |
|
|
|
0,70 |
|
|
|
0,86 |
Дискретная
случайная величина X задана
законом распределения вероятностей:
 Тогда
ее среднее квадратическое отклонение
равно …
Тогда
ее среднее квадратическое отклонение
равно …
|
|
|
0,80 |
|
|
|
0,64 |
|
|
|
2,60 |
|
|
|
14,16 |
Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …
|
|
|
0,57 |
|
|
|
0,43 |
|
|
|
0,55 |
|
|
|
0,53 |
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Площадь
параллелограмма, построенного на
векторах ![]() и
и ![]() ,
равна …
,
равна …
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
6 |
Модуль
градиента скалярного поля ![]() в
точке пересечения оси
в
точке пересечения оси ![]() с
поверхностью
с
поверхностью ![]() равен
…
равен
…
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
Норма
вектора ![]() ,
, ![]() в
евклидовом пространстве со стандартным
скалярным произведением равна 5
при
в
евклидовом пространстве со стандартным
скалярным произведением равна 5
при ![]() равном
…
равном
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Объем
пирамиды, построенной на векторах ![]() ,
, ![]() и
и ![]() ,
равен …
,
равен …
|
|
|
14 |
|
|
|
84 |
|
|
|
28 |
|
|
|
42 |
Если
функция
непрерывна
на отрезке ![]() ,
то интеграл
,
то интеграл  можно
представить в виде …
можно
представить в виде …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Промежуток
возрастания функции  имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Множество
первообразных функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор является линейной комбинацией векторов и , если , то равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
– 2 |
|
|
|
– 3 |
Базисное
решение системы  может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Корень
уравнения 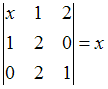 равен
…
равен
…
|
|
|
– 3 |
|
|
|
0 |
|
|
|
3 |
|
|
|
– 9 |
Отображение ![]() действует
по правилу:
действует
по правилу:  Тогда
Тогда ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны
три множества: ![]() ,
, ![]() и
и ![]() .
Тогда число элементов множества
.
Тогда число элементов множества ![]() равно …
равно …
|
1
| |
Асимптоты
гиперболы ![]() задаются
уравнениями …
задаются
уравнениями …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее
уравнение плоскости, проходящей через
точку ![]() параллельно
плоскости
параллельно
плоскости ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сфера
с центром ![]() проходит
через точку
проходит
через точку ![]() .
Тогда ее уравнение имеет вид …
.
Тогда ее уравнение имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны два множества: и . Тогда количество целых значений , принадлежащих пересечению множеств и , равно …
|
4
| |
Мера
плоского множества ![]() равна
…
равна
…
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
0 |
Отображение
действует
по правилу:  Тогда
имеет
вид …
Тогда
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интерполяционный
многочлен Лагранжа второй степени ![]() может
быть составлен по таблице значений
функции
может
быть составлен по таблице значений
функции ![]() вида
…
вида
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение
дифференцируемой функции
в
точке ![]() можно
приближенно найти как …
можно
приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методом
Эйлера с шагом ![]() решается
задача Коши для системы дифференциальных
уравнений
решается
задача Коши для системы дифференциальных
уравнений 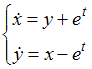 с
начальными условиями
с
начальными условиями ![]() ,
, ![]() .
Тогда значения искомых функций
.
Тогда значения искомых функций ![]() и
и ![]() равны
…
равны
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поверхность 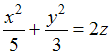 пересекается
с плоскостью
пересекается
с плоскостью ![]() по
…
по
…
|
|
|
параболе |
|
|
|
эллипсу |
|
|
|
гиперболе |
|
|
|
двум пересекающимся прямым |
Вершина
параболы ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мИз
генеральной совокупности извлечена
выборка объема ![]() :
:
 Тогда
выборочное среднее квадратическое
отклонение равно …
Тогда
выборочное среднее квадратическое
отклонение равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее
уравнение плоскости, проходящей через
точку ![]() перпендикулярно
прямой
перпендикулярно
прямой ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из
генеральной совокупности извлечена
выборка объема ![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
 Тогда
число вариант
Тогда
число вариант ![]() в
выборке равно …
в
выборке равно …
|
|
|
32 |
|
|
|
82 |
|
|
|
8 |
|
|
|
31 |
Соотношением вида можно определить …
|
|
|
левостороннюю критическую область |
|
|
|
правостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна 3,5. Тогда его интервальная оценка может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Смешанное
произведение векторов ![]() ,
, ![]() и
и ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны два вектора: и , где , , угол между векторами и равен . Тогда площадь треугольника, построенного на векторах и будет равна …
|
|
|
2,5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
Положительно определенная квадратичная форма может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
невырожденной квадратной матрицы ![]() решение
системы
решение
системы ![]() в
матричной форме имеет вид …
в
матричной форме имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель  равен
…
равен
…
|
|
|
45 |
|
|
|
135 |
|
|
|
– 45 |
|
|
|
– 135 |
Линейно зависимыми будут вектора …
|
|
|
|
|
|
|
,
, |
|
|
|
,
, |
|
|
|
,
, |
Множество
первообразных функции  имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Промежуток убывания функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для функции точка является точкой …
|
|
|
разрыва первого рода |
|
|
|
разрыва второго рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Среднее значение функции на отрезке равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В урне находятся 10 белых, 15 красных, 20 голубых шаров. Все шары пронумерованы. Сколькими различными способами можно взять из урны три шара разных цветов?
|
3000
| |
Даны
множества ![]() и
и ![]() ,
тогда количество пар, удовлетворяющих
бинарному отношению
,
тогда количество пар, удовлетворяющих
бинарному отношению ![]() равно …
равно …
|
|
|
6 |
|
|
|
4 |
|
|
|
7 |
|
|
|
12 |
Таблица
истинности для формулы ![]() представляет
собой …
представляет
собой …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрица
смежности  соответствует
графу …
соответствует
графу …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проводится
n независимых
испытаний, в каждом из которых вероятность
появления события A постоянна
и равна 0,6. Тогда математическое
ожидание ![]() и
дисперсия
и
дисперсия ![]() дискретной
случайной величины X –
числа появлений события A в
дискретной
случайной величины X –
числа появлений события A в ![]() проведенных
испытаниях равны …
проведенных
испытаниях равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 5 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет белым, равна …
|
|
|
0,47 |
|
|
|
0,55 |
|
|
|
0,35 |
|
|
|
0,50 |
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
значения a и
b могут
быть равны …
Тогда
значения a и
b могут
быть равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное решение линейного неоднородного дифференциального уравнения второго порядка имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий интеграл дифференциального уравнения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если  ,
то
,
то ![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
Частное от деления двух комплексных чисел и равно …
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Система  решается
матричным способом по формуле
решается
матричным способом по формуле ![]() ,
где
,
где ![]() ,
–
матрица свободных членов. Тогда
,
–
матрица свободных членов. Тогда ![]() –
матрица, обратная к матрице системы
,
имеет вид …
–
матрица, обратная к матрице системы
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Банк выдает 70% всех кредитов юридическим лицам, а 30% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило юридическое лицо, равна …
|
|
|
0,875 |
|
|
|
0,125 |
|
|
|
0,105 |
|
|
|
0,375 |
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
|
|
|
0,0081 |
|
|
|
0,081 |
|
|
|
0,06 |
|
|
|
0,0729 |
Уравнение окружности с центром в начале координат радиуса 5 в полярных координатах имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расстояние
между фокусами гиперболы  равно
…
равно
…
|
|
|
10 |
|
|
|
7 |
|
|
|
5 |
|
|
|
2,5 |
Уравнение
поверхности второго порядка ![]() определяет
…
определяет
…
|
|
|
эллипсоид |
|
|
|
параболоид |
|
|
|
конус |
|
|
|
однополостный гиперболоид |
Норма
вектора ![]() в
евклидовом пространстве со стандартным
скалярным произведением равна …
в
евклидовом пространстве со стандартным
скалярным произведением равна …
|
|
|
3 |
|
|
|
1 |
|
|
|
9 |
|
|
|
5 |
Даны
два вектора: ![]() и
и ![]() ,
где
,
,
где
, ![]() ,
угол между векторами
и
равен
,
угол между векторами
и
равен ![]() .
Тогда площадь параллелограмма,
построенного на векторах
и
,
будет равна …
.
Тогда площадь параллелограмма,
построенного на векторах
и
,
будет равна …
|
|
|
14 |
|
|
|
|
|
|
|
7 |
|
|
|
|
Градиент
скалярного поля ![]() равен
нулевому вектору в точке …
равен
нулевому вектору в точке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если и , то производная функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если ![]() и
и ![]() –
корни квадратного уравнения
–
корни квадратного уравнения ![]() ,
то
,
то ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель системы равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке: удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базисное решение системы может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линейно зависимыми будут вектора …
|
|
|
, , |
|
|
|
, , |
|
|
|
, , |
|
|
|
, , |
Положительно определенная квадратичная форма может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель равен …
|
|
|
45 |
|
|
|
135 |
|
|
|
– 45 |
|
|
|
– 135 |
Если
все варианты ![]() исходного
вариационного ряда увеличить в два
раза, то выборочная дисперсия
исходного
вариационного ряда увеличить в два
раза, то выборочная дисперсия ![]() …
…
|
|
|
увеличится в четыре раза |
|
|
|
увеличится в два раза |
|
|
|
не изменится |
|
|
|
увеличится на четыре единицы |
Статистическое
распределение выборки имеет вид
 Тогда
значение относительной частоты
Тогда
значение относительной частоты ![]() равно
…
равно
…
|
|
|
0,25 |
|
|
|
0,05 |
|
|
|
0,26 |
|
|
|
0,75 |
Дан
доверительный интервал ![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при увеличении надежности
(доверительной вероятности) оценки
доверительный интервал может принять
вид …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при увеличении надежности
(доверительной вероятности) оценки
доверительный интервал может принять
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
проверки нулевой гипотезы ![]() при
заданном уровне значимости
при
заданном уровне значимости ![]() выдвинута
конкурирующая гипотеза
выдвинута
конкурирующая гипотеза ![]() .
Тогда область принятия гипотезы может
иметь вид …
.
Тогда область принятия гипотезы может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отображение действует по правилу: Тогда имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны три множества: , и . Тогда число элементов множества равно …
|
1 | |
Функция
представлена
таблицей:
 Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …
Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …
|
|
|
5,5 |
|
|
|
11 |
|
|
|
6 |
|
|
|
0 |
Метод
левых прямоугольников дает приближенное
значение интеграла 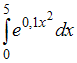 …
…
|
|
|
с недостатком |
|
|
|
с избытком |
|
|
|
точно |
|
|
|
про которое ничего определенного сказать нельзя |
Уравнение ![]() решается
методом касательных (Ньютона). Корень
принадлежит интервалу
решается
методом касательных (Ньютона). Корень
принадлежит интервалу ![]() .
Тогда первое приближение
к
точному корню
будет
равно …
.
Тогда первое приближение
к
точному корню
будет
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На отрезке задано дифференциальное уравнение . Значение производной в точке может быть заменено выражением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное решение дифференциального уравнения может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее решение линейного неоднородного дифференциального уравнения второго порядка имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциальное
уравнение ![]() будет
уравнением с разделяющимися переменными
при значении
,
равном …
будет
уравнением с разделяющимися переменными
при значении
,
равном …
|
|
|
4 |
|
|
|
0 |
|
|
|
2 |
|
|
|
1 |
Частное
решение дифференциального уравнения ![]() ,
удовлетворяющее условию
,
удовлетворяющее условию ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Бинарное
отношение ![]() задано
на рисунке
задано
на рисунке
 Тогда
из трех матриц:
Тогда
из трех матриц:
 ;
;
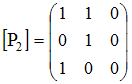 ;
;
 соответствует
матрице бинарного отношения матрица
…
соответствует
матрице бинарного отношения матрица
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не соответствует ни одна из представленных матриц |
На 10 карточках написаны буквы так, что из этих карточек можно получить слово ИСЧИСЛЕНИЕ. Сколько существует различных 10-буквенных слов, которые можно образовать с помощью этих десяти карточек?
|
151200 | |
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке: удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель
системы  равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка
разрыва функции 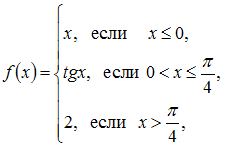 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 6 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Непрерывная
случайная величина
задана
плотностью распределения вероятностей:
 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основная гипотеза имеет вид . Тогда конкурирующей может являться гипотеза …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна …
|
|
|
6,38 |
|
|
|
6,42 |
|
|
|
6,1 |
|
|
|
6,4 |
Даны
множества: ![]() и
и ![]() .
Тогда число элементов, принадлежащих
их пересечению равно …
.
Тогда число элементов, принадлежащих
их пересечению равно …
|
3 |
Функция , где – действительные числа, …
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме треугольника |
Прообразом
множества ![]() при
отображении
является
…
при
отображении
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система  будет …
будет …
|
|
|
совместной и неопределенной |
|
|
|
несовместной и неопределенной |
|
|
|
совместной и определенной |
|
|
|
несовместной и определенной |
Матрица
квадратичной формы ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
За базис четырехмерного векторного пространства можно принять совокупность векторов …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложение
определителя 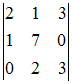 по
строке может иметь вид …
по
строке может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Не является эквивалентным отношение …
|
|
|
включения множеств |
|
|
|
подобия плоских фигур |
|
|
|
равенства чисел |
|
|
|
коллинеарности векторов |
В организации работают 2 курьера. Тогда существует ___ способа(-ов) послать 5 писем в 5 различных организаций.
|
32
| |
Для
графа, изображенного на
рисунке,
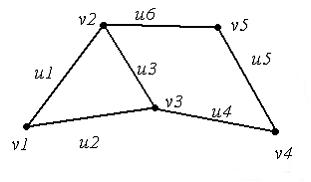 последовательность
последовательность ![]() является …
является …
|
|
|
маршрутом |
|
|
|
цепью |
|
|
|
циклом |
|
|
|
деревом |
Если ![]() и
–
ортогональные векторы из евклидова
пространства со стандартным скалярным
произведением, такие что
и
–
ортогональные векторы из евклидова
пространства со стандартным скалярным
произведением, такие что ![]() ,
, ![]() ,
то норма вектора
,
то норма вектора ![]() равна
…
равна
…
|
|
|
5 |
|
|
|
25 |
|
|
|
1 |
|
|
|
– 1 |
Смешанное
произведение ![]() векторов
векторов ![]() ,
, ![]() и
и ![]() равно
5 при значении
равном
…
равно
5 при значении
равном
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Модуль градиента скалярного поля в точке равен …
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
4 |
Площадь треугольника с вершинами в точках , и равна …
|
|
|
7,5 |
|
|
|
15 |
|
|
|
5 |
|
|
|
2,5 |
На рисунке изображен график функции : Тогда корень уравнения отделен на отрезке …
|
|
|
[–1; 1] |
|
|
|
[2; 4] |
|
|
|
[–4; 6] |
|
|
|
[–3; –1] |
Интерполяционный
многочлен Лагранжа, составленный по
таблице значений функции
 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На отрезке задано дифференциальное уравнение . Значение производной в точке может быть заменено выражением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение определенного интеграла по формуле парабол (Симпсона) можно приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное
решение дифференциального уравнения  ,
удовлетворяющее условию
,
удовлетворяющее условию  ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий интеграл дифференциального уравнения при имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное
решение
линейного
неоднородного дифференциального
уравнения второго порядка ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциальное уравнение будет уравнением с разделяющимися переменными при значении , равном …
|
|
|
4 |
|
|
|
0 |
|
|
|
2 |
|
|
|
1 |
Мнимая
полуось гиперболы ![]() равна …
равна …
|
|
|
3 |
|
|
|
36 |
|
|
|
6 |
|
|
|
9 |
Уравнение
сферы имеет вид ![]() .
Тогда радиус сферы равен …
.
Тогда радиус сферы равен …
|
|
|
7 |
|
|
|
19 |
|
|
|
10 |
|
|
|
49 |
Плоскости ![]() и
и ![]() перпендикулярны
при значении
перпендикулярны
при значении ![]() ,
равном …
,
равном …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Одна
из вершин треугольника находится в
полюсе ![]() ,
две другие имеют координаты
,
две другие имеют координаты  и
и  .
Тогда площадь треугольника
.
Тогда площадь треугольника ![]() равна …
равна …
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,6. Тогда математическое ожидание и дисперсия дискретной случайной величины X – числа появлений события A в проведенных испытаниях равны …
|
|
|
, |
|
|
|
, |
|
|
|
, |
|
|
|
, |
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
|
|
|
0,0081 |
|
|
|
0,081 |
|
|
|
0,06 |
|
|
|
0,0729 |
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Даны
множества
и
.
Тогда количество пар, удовлетворяющих
бинарному отношению ![]() равно …
равно …
|
|
|
3 |
|
|
|
4 |
|
|
|
2 |
|
|
|
12 |
Для функции , заданной таблицей, СДНФ имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В урне находятся 5 белых, 7 красных, 6 голубых шаров. Сколько существует способов извлечь 9 шаров так, чтобы среди них оказалось 2 белых, 3 красных и 4 голубых шара?
|
5250 | |
Определенный интеграл равен …
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
Множество первообразных функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Материальная
точка движется прямолинейно по закону ![]() .
Тогда ускорение точки в момент
времени
.
Тогда ускорение точки в момент
времени ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция  не
является непрерывной на отрезке …
не
является непрерывной на отрезке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение производной функции в точке равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение
выражения ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Корень
уравнения  равен
…
равен
…
|
|
|
– 1 |
|
|
|
– 5 |
|
|
|
1 |
|
|
|
5 |
Система  не
имеет решений, если
равно
…
не
имеет решений, если
равно
…
|
|
|
– 2 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
Линейно зависимыми будут вектора …
|
|
|
, , |
|
|
|
, , |
|
|
|
, , |
|
|
|
, , |
Уравнение поверхности второго порядка определяет …
|
|
|
эллипсоид |
|
|
|
параболоид |
|
|
|
конус |
|
|
|
однополостный гиперболоид |
Точка задана в прямоугольной системе координат. Тогда ее полярные координаты равны …
|
|
|
, |
|
|
|
, |
|
|
|
, |
|
|
|
, |
Уравнение
плоскости, проходящей через
точку ![]() параллельно
векторам
параллельно
векторам ![]() и
и ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вершина параболы имеет координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное решение линейного неоднородного дифференциального уравнения второго порядка имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны два вектора: и , где , , угол между векторами и равен . Тогда площадь параллелограмма, построенного на векторах и , будет равна …
|
|
|
14 |
|
|
|
|
|
|
|
7 |
|
|
|
|
Модуль градиента скалярного поля в точке равен …
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
4 |
Точки , , и лежат в одной плоскости, если параметр равен …
|
|
|
2 |
|
|
|
0 |
|
|
|
1 |
|
|
|
– 2 |
Даны
векторы
и ![]() ,
угол между которыми равен
,
угол между которыми равен ![]() .
Тогда проекция вектора
на
вектор
равна …
.
Тогда проекция вектора
на
вектор
равна …
|
|
|
|
|
|
|
– 1 |
|
|
|
3 |
|
|
|
|
Даны
два множества: ![]() и
и ![]() .
Тогда количество целых значений
,
принадлежащих разности множеств
\
,
равно …
.
Тогда количество целых значений
,
принадлежащих разности множеств
\
,
равно …
|
4 |
Мера
плоского множества ![]() равна
…
равна
…
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
Прообразом множества при отображении является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Не
может служить метрикой
пространства ![]() функция …
функция …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид: Тогда относительная частота варианты в выборке равна …
|
|
|
0,05 |
|
|
|
0,06 |
|
|
|
0,25 |
|
|
|
0,20 |
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …
|
|
|
11,25 |
|
|
|
19,5 |
|
|
|
15 |
|
|
|
21,25 |
Функция ![]() представлена
таблицей
представлена
таблицей
 Тогда
значение
Тогда
значение ![]() ,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
– 3 |
|
|
|
14 |
|
|
|
|
|
|
|
– 8 |
Для
задачи Коши ![]() выполнен
один шаг получения приближенного решения
методом Эйлера с шагом
.
Тогда точка
выполнен
один шаг получения приближенного решения
методом Эйлера с шагом
.
Тогда точка ![]() ломаной
Эйлера …
ломаной
Эйлера …
|
|
|
расположена ниже приближаемой интегральной кривой |
|
|
|
расположена выше приближаемой интегральной кривой |
|
|
|
принадлежит приближаемой интегральной кривой |
|
|
|
может лежать как выше, так и ниже приближаемой интегральной кривой |
Значение дифференцируемой функции в точке можно приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рисунке изображен график функции : Тогда корень уравнения отделен на отрезке …
|
|
|
[–1; 1] |
|
|
|
[2; 4] |
|
|
|
[–4; 6] |
Тема: Неориентированные графы
Начало формы
Конец формы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция представлена таблицей Тогда значение , вычисленное с помощью интерполяционного многочлена Лагранжа, равно …
|
|
|
– 3 |
|
|
|
14 |
|
|
|
|
|
|
|
– 8 |
Начало формы
Конец формы
Биективное
отображение отрезка
на
отрезок
![]() может
быть задано функцией …
может
быть задано функцией …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция
 ,
заданная на множестве натуральных чисел
…
,
заданная на множестве натуральных чисел
…
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме треугольника |
Значение
производной функции
![]() в
точке
равно
…
в
точке
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное комплексных чисел и равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К
графику функции
![]() в
его точке с абсциссой
в
его точке с абсциссой
![]() проведена
касательная. Тогда площадь треугольника,
образованного касательной и отрезками,
отсекаемыми ею на осях координат, равна
…
проведена
касательная. Тогда площадь треугольника,
образованного касательной и отрезками,
отсекаемыми ею на осях координат, равна
…
|
|
|
|
|
|
|
|
|
|
|
|
Значение
определенного интеграла
 принадлежит
промежутку …
принадлежит
промежутку …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скалярное произведение векторов и равно 8, угол между векторами равен , норма вектора равна 4. Тогда норма вектора равна …
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
3 |
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – десять, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Общее
решение дифференциального уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
Одна из вершин треугольника находится в полюсе , две другие имеют координаты и . Тогда площадь треугольника равна …
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
Уравнение плоскости, проходящей через точку параллельно векторам и , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
 Тогда
несмещенная оценка математического
ожидания равна …
Тогда
несмещенная оценка математического
ожидания равна …
|
|
|
13,14 |
|
|
|
13,0 |
|
|
|
13,34 |
|
|
|
13,2 |
Определитель системы равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение
производной функции
![]() в
точке
равно
…
в
точке
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Промежуток возрастания функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для
определенного интеграла
 справедливо
равенство
справедливо
равенство
Для
функции
![]() точка
точка
![]() является
точкой …
является
точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Метод Гаусса для решения систем линейных уравнений заключается …
|
|
|
в последовательном исключении переменных |
|
|
|
в последовательном исключении свободных членов |
|
|
|
в нахождении обратной матрицы |
|
|
|
в вычислении вспомогательных определителей системы |
Для
задачи Коши
выполнен
один шаг получения приближенного решения
методом Эйлера - Коши с шагом
:
 Тогда
значение
Тогда
значение
![]() ,
записанное с двумя знаками после запятой,
равно …
,
записанное с двумя знаками после запятой,
равно …
|
|
|
1,12 |
|
|
|
0,9155 |
|
|
|
1,11 |
|
|
|
1,1155 |
В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мера
плоского множества
![]() ,
где А=
,
где А=![]() и
и
![]() равна
…
равна
…
|
|
|
|
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Функция
 заданная
на множестве целых чисел …
заданная
на множестве целых чисел …
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме треугольника |
Уравнение окружности с центром в начале координат радиуса 5 в полярных координатах имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Даны два вектора: и , где , , угол между векторами и равен . Тогда площадь параллелограмма, построенного на векторах и , будет равна …
|
|
|
14 |
|
|
|
|
|
|
|
7 |
|
|
|
|
Общий
вид частного решения
линейного
неоднородного дифференциального
уравнения второго порядка
![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|













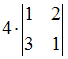
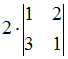





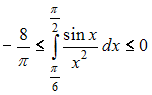


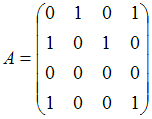





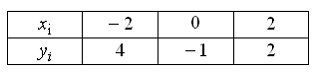







 ,
, ,
,  ,
,