Гомогенный реактор с отражателем в двухгрупповом приближении

Условие критичности.

Некоторые эффекты влияния отражателя на характерис­тики реактора были проиллюстрированы на примере одногруппового приближения. Однако полученные результаты недоста­точно точны, поскольку характерные изменения спектра нейтро­нов, которые имеют место вблизи поверхности раздела активной зоны и отражателя, не учитывались. Этот недостаток одногруппового приближения можно исправить, решая задачу, по крайней мере, в малогрупповом приближении. Одним из широко применяемых методов определения критических размеров реакторов на тепловых нейтронах является двухгрупповое при­ближение. Эта модель проста по физическому содержанию и позволяет во многих случаях добиться необходимой точности расчетов.

Двухгрупповая модель предполагает, что поведение быстрых нейтронов (Е>Е_гр) в реакторе с отражателем может быть опи­сано с помощью одного диффузионного уравнения (одной группы нейтронов) при подоб­ранных должным образом групповых константах.

Тепловые нейтроны (Е<Е_гр) объединяются во вторую энер­гетическую группу.

Таким образом, в случае применения указанной модели к многозонному реактору записываются два диффузионных уравнения для каждой зоны: одно для описания быстрых ней­тронов (индекс «б») и второе — для описания тепловых нейтро­нов (индекс «т») совместно с граничными условиями. В случае реактора с отражателем групповые диффузионные уравнения для быстрых и тепловых нейтронов запишем в форме:

а) для активной зоны

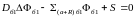
В общем случае:

Здесь:

б) для отражателя:

На границе активной зоны и отражателя (r = R) для быст­рых и тепловых нейтронов имеем следующие условия:

Потоки Ф_б2 и Ф_Т2 обращаются в нуль на экстраполирован­ной границе отражателя R_э.

Для нахождения условия критичности необходимо воспользоваться граничными условиями и выражениями для потоков быстрых и тепловых нейтронов в активной зоне и отражателе. Тогда можно получить систему алге­браических линейных однородных уравнений, решение которой имеет смысл только в случае, если ее определитель равен нулю.

Это равенство представляет собой условие критичности реактора с отражателем в двухгрупповом приближении. Напомним, что рассматривается простейшая задача,— одно­родная активная зона и однородный отражатель.

На следующем рисунке в качестве иллюстрации приведен качественный характер распределения потоков быстрых и тепловых нейтронов в активной зоне и отра­жателе. Значения Ф_б и Ф_т в центре активной зоны нормиро­ваны на единицу.

Пространственное распределение плотностей потоков тепловых и быстрых нейтронов в активной зоне и отражателе.

Для нейтронов тепловых энергий в обла­сти, близкой к отражателю наблюдается от­клонение от основной функции (Х₁). Этот эффект особенно резко выражен в реакторах с во­дяным замедлителем и Be- или D₂O-отражателями. В реакторах небольших размеров с таким составом максимальный поток тепловых нейтронов в отражателе бывает даже значительно выше максимального потока в центре активной зоны. Такой характер распределения по­тока объясняется тем, что при незначительном различии в скоростях генерации тепло­вых нейтронов ско­рость их поглощения в среде активной зоны во много раз выше (де­сятки раз) скорости поглощения в отражателе. Максимальное значение потока тепловых ней­тронов в отражателе располо­жено от границы активной зоны примерно на расстоянии длины замедления в отража­теле ( ).