
- •1. Конструктивная схема ядерного реактора.
- •Общий принцип работы ядерного реактора
- •3. Влияние размеров реактора на Кэф.
- •4. Влияние поглощения нейтронов
- •5. Поколение нейтронов в яр
- •6. Эффективный коэффициент размножения, реактивность
- •2. Гомогенный реактор без отражателя в одногрупповом приближении
- •2.1 Уравнение реактора в одногрупповом приближении
- •2.2 Условие критичности гомогенного реактора без отражателя в одногрупповом приближении.
- •Критические размеры реактора цилиндрической формы
- •2.4. Результат решения волнового уравнения для цилиндрической гомогенной активной зоны.
- •2.5. Выражение для геометрического параметра цилиндрической активной зоны.
- •2.6. Оптимальное соотношение размеров цилиндрической активной зоны.
- •Краткие выводы
- •2.7. Критические размеры цилиндрического яр
- •2.8. Коэффициенты неравномерности распределения плотности потока нейтронов в цилиндрическом яр
- •2.9. Результаты анализа яр других геометрий
- •2. Яр в форме прямоугольный параллелепипед
- •3. Яр в форме цилиндра
- •4. Яр в форме сферы
- •2.10. Принципиальные подходы к проектированию реакторов
- •9.2. Эффективная добавка (э)
- •Эффективные размеры активной зоны яр с отражателем. Эквивалентный яр
- •1. Ядерное топливо.
- •2. Замедлитель.
- •3. Теплоноситель
- •4. Параметры структуры активных зон гетерогенных яр.
- •2. Гомогенный реактор с отражателем в одногрупповом приближении
- •2.1. Влияние отражателя на нейтронно-физические свойства акт. Зоны
- •2.2 Требования к материалу отражателя
- •2.3. Математическая постановка задачи о гомогенном реакторе с отражателем в одногрупповом приближении
- •2.4 Ядерный реактор в форме бесконечной пластины с отражателем
- •2.5. Цилиндрический яр с боковым отражателем в одногрупповом приближении
- •2.6. Эффективные размеры активной зоны яр с отражателем. Эквивалентный яр
- •10.2. О распределении нейтронов в слабо размножающих средах
- •Гомогенный реактор с отражателем в двухгрупповом приближении
- •Многогрупповой подход
- •Сущность метода многих групп
- •Многогрупповое уравнение
- •Многогрупповое уравнение диффузии. Баланс нейтронов.
- •Системы групповых констант.
- •Библиотеки констант. Выбор ширин групп
- •Библиотека констант бнаб
- •Эффективность центрального стержня в зависимости от глубины погружения в реактор
- •Эффективность эксцентрично расположенного стержня в зависимости от глубины погружения в реактор
- •Физические характеристики уран-водных ячеек
2.6. Эффективные размеры активной зоны яр с отражателем. Эквивалентный яр
Размеры активной зоны, определенные с учетом эффективной добавки, называются эффективными размерами АЗ. Например, для реактора в форме бесконечной пластины эффективные размера АЗ составляют: Hэф = H +2δ. Так как при эффективных размерах АЗ является критичной, то проводя критический анализ, можно воспользоваться расчетной моделью – эквивалентным ЯР. Эквивалентный ЯР – это реактор, имеющий эффективные размеры. Использование этой модели позволяет перейти при анализе АЗ от ЯР с отражателем к ЯР без отражателя. При этом для такого ЯР будет выполняться условие критичности реактора без отражателя (равенство материального и геометрического параметров) при условии использования в геометрическом параметре не геометрических, а эффективных размеров АЗ. Например, для цилиндрической АЗ в ЯР с отражателем с размерами H и R эффективные размеры равны:
Hэф = H + 2δ; Rэф = R + δ,
геометрический параметр определится зависимостью:
,
а эффективный коэффициент размножения – известным выражением:
.
Такой подход значительно облегчает решение задач и будет использоваться в дальнейшем (например, курсовой проект).
Так как в эквивалентном ЯР потоки нейтронов на границе должны обращаться в нуль, то становится ясен физический смысл эффективной добавки. Это расстояние, отсчитываемое от границы АЗ в отражатель, на котором аналитическое продолжение распределения потока нейтронов в АЗ реактора с отражателем обращается в нуль. Однако такое определение справедливо лишь в случае одногруппового приближения, когда влияние отражателя (наличие переходных областей) не учитывается. В общем случае, когда идет учет влияния отражателя, эффективная добавка более строго будет иметь физический смысл: это расстояние, отсчитываемое от границы АЗ в отражатель, на котором аналитическое продолжение асимптотического распределения потока нейтронов обращается в нуль.
Сферический ЯР с отражателем
Р ассмотрим сферический ЯР, состоящий из АЗ радиусом R, окруженной отражателем толщиной Т.
Порядок определения потоков нейтронов в АЗ и в отражателе остается тот же, что и в предыдущих случаях.
Записывается
уравнение ЯР отдельно для отражателя
и АЗ.

 где
- материальный параметр АЗ (
);
- формальный материальный параметр для
отражателя (
);
оператор
в сферических координатах без учета
угловых зависимостей имеет вид:
где
- материальный параметр АЗ (
);
- формальный материальный параметр для
отражателя (
);
оператор
в сферических координатах без учета
угловых зависимостей имеет вид:
Решаются уравнения относительно и и используются граничные условия. В результате чего записывается условие критичности:
(1)
Введя эффективную добавку за счет отражателя , имеем, что ; ;
Тогда левая часть (1) примет вид:
Т.о. окончательно условие критичности имеет вид:
(2)
Из
условия (1) легко получить выражение для
сферического ЯР без отражателя, положив
Т=0. В этом случае правая часть (1) стремится
к бесконечности и

 ;
;
 (геометрический параметр сферического
ЯР без отражателя).
(геометрический параметр сферического
ЯР без отражателя).
Если рассмотреть условие (2), то при . Снова получена реальная картина ЯР без отражателя.
Проведем
преобразования выражения (2), разделив
обе части на
 :
:

Вынесем
в правой части за скобку
 :
:


Приведем
полученное выражение к удобному для
анализа виду, вынеся в правой части за
скобку
 :
:
 (3)
(3)
Отсюда в общем случае:

Положим, что D1=D2, тогда:
 (4)
(4)
Рассмотри
большой сферический ЯР, размеры которого
R>>
 .
Тогда
.
Тогда
 .
Т.к.
- ограничено
.
Т.к.
- ограничено

 Вернемся
к выражению (3) и проанализируем его для
большого ЯР.
Вернемся
к выражению (3) и проанализируем его для
большого ЯР.
Разлагая
левую часть (3) в ряд вследствие малости
 ограничиваемся одним членом разложения
():
ограничиваемся одним членом разложения
():
Для больших ЯР , тогда:
Используя условия (*) имеем, что второе слагаемое правой части стремится к нулю, отсюда:
Т.о. для больших сферических ЯР условие критичности совпадает с теми, что были получены ранее. (Анализ этих условий провести самостоятельно, аналогично плоскому ЯР).
Макроскопическое сечение утечки.
Возьмем для примера сферический реактор.
Если известен коэффициент k, то шар может быть реактором только в случае k>1. При выполнении этого условия найдем положительное значение В2 и экстраполированный размер шара RЭ = π/В, необходимый для осуществления в шаре стационарной цепной ядерной реакции. Реальный размер критического реактора будет несколько меньше, чем RЭ. Значит, если из того же материала сделать шар радиусом RЭ, то получится реактор с некоторым превышением Кэф над единицей (с положительной реактивностью).
Геометрический параметр:
B2 = (π/Rэ)2 (10.9)
и К0 - значение коэффициента k, необходимое для осуществления стационарной цепной ядерной реакции. Значение К0 найдем по формуле

Для вероятности избежать утечки тепловых нейтронов можно записать:
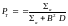
Анализируя эту формулу можно отметить, что величина DB2 играет роль «макроскопического сечения утечки».
Из тепловой группы нейтроны выбывают только двумя путями: или поглощаются, или «утекают». Следовательно, отношение Σа/(Σа+DB2) есть доля поглощаемых нейтронов по отношению ко всем выбывающим из группы нейтронам или, говоря иначе, вероятность избежания утечки во время пребывания в тепловой группе.
При этом отношение Σf/Σа есть вероятность для всех поглощаемых нейтронов быть захваченными в делящемся нуклиде с последующим делением ядра. Вероятность поглощения с делением ядра для всех нейтронов группы будет равна произведению этих двух вероятностей, т.е. отношению Σf/(Σа+DB2).
