2.5. Замыкание множества атрибутов относительно множества функциональных зависимостей

Пусть дано X R – множество атрибутов, система функциональных зависимостей f.

- замыкание множества атрибутов по множеству функциональных зависимостей.

Пример.

,

X=AE,

.

1. Выписывается множество атрибутов (текущее).

2. Каждая ФЗ проверяется на предмет включения ее в левой части в текущее множество атрибутов.

3. Если включается левая часть, то в текущее множество атрибутов добавляется правая часть функциональной зависимости, кроме тех атрибутов, которые есть в текущем множестве атрибутов.

4. Если в результате повторной проверки всех функциональных зависимостей, ни одна из ФЗ не добавит элементов в текущее множество атрибутов, то текущее множество атрибутов становится замыканием.

.

Теорема. Функциональная зависимость выводима из множества функциональных зависимостей f тогда и только тогда, когда замыкание атрибутов левой части этой зависимости по f включает в себя ее правую часть.

.

Доказательство. Пусть

,

.

Докажем с помощью аксиомы проективности.

1) - не выполняется;

2) - выполняется, AX AXY= .

Обратное доказывается аналогично с помощью аксиомы аддитивности.

2.6. Эквивалентность двух систем функциональных зависимостей

Две системы q и f двух функциональных зависимостей эквивалентны тогда и только тогда, когда все функциональные зависимости из q выводятся из f и все функциональные зависимости из f выводятся из q.

f≡q ≡ (f q & q f).

Пример. Множества f= и g= эквивалентны.

f |= A→BCE,

f |= A→ABD,

f |= CD→E,

g |= A→BC,

g |= A→D,

g |= CD→E.

1) A→BCE |= A→BC,

A ABCED= .

2) A→D |= A→ABD,

=ABD.

3) =A ABC ABCD ABCDE,

=ABCD.

2.7 Метод синтеза

1. Построение неизбыточного покрытия.

Покрытие является неизбыточным, если из него нельзя удалить ни одной функциональной зависимости, не нарушая эквивалентности системы.

, ,

где - все оставшиеся зависимости от f или , то есть g |= x→y.

≡ .

2. Левая редукция.

, .

Множество функциональных зависимостей леворедуцированно, если нельзя удалить из левой части ни одного атрибута.

3. Правая редукция.

≡ .

.

g |= X→A.

Множество функциональных зависимостей праворедуцированно, если нельзя удалить из правой части ни одного атрибута.

Пример.

,

,

.

.

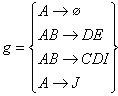2.8. Классы эквивалентности функциональных зависимостей с эквивалентными левыми частями

Имеем два множества атрибутов X и Y и множество функциональных зависимостей f. X и Y эквивалентны относительно f в том случае, если выполняется f |= X→Y & f |= Y→X.

Если есть зависимости X→Y и V→W в f и множества X и V эквивалентны, то эти две зависимости называются зависимостями с эквивалентными левыми частями.

На основе введенных отношений эквивалентности множество функциональных зависимостей разбивается на классы эквивалентности.

E_f (AB) - класс эквивалентности функциональных зависимостей, у которых левые части эквивалентны AB

.

E_f (A) = {A→BC, B→A}.

E_f (AD) = {AD→E}.

Этап построения классов эквивалентности определяет минимальное количество таблиц, а именно каждый класс эквивалентности составляет одну таблицу.

В первом приближении функциональные зависимости , входящие в первый класс эквивалентности, определяют множество ключей для первой таблицы.

Построение минимального покрытия:

, ,

f≡g.

Критерий.

f≡g <=> |= X→V.

Пример.

,

E_f (A) = {A→BC, B→A}.

E_f (AD) = {AD→E, BD→J}.

f \ E_f (A) |= A→B <=> -не верно.

f \ E_f (AD) |= AD→BD.

AD ADBC,

.