2. Скласти математичну модель ізотермічного реактора ріп (в статичному режимі), в якому протікає реакція типу:

_{k1 k2}

A  P  S

С_Авх, v – задано, С_Pвх, С_Sвх = 0.

У статичному ізотермічному режимі процес в РІП можна описати рівнянням матеріального балансу:

Тоді математична модель РІП для даної реакції матиме вигляд:

Зробивши перегрупування відносно початкових концентрацій, приведемо систему до вигляду:

3. Основні поняття теорії експерименту, класифікація методів математичного моделювання, експериментально-статистичне моделювання.

Математичне моделювання – метод наукового дослідження, який оснований на пізнанні процесів за допомогою математичних моделей і базується на ідентичності рівнянь, що описують явище в моделі та оригіналі.

До методів математичного моделювання відносять детермінований (аналітичний або структурний) підхід та експериментально-статистичний (стохастичний) підхід моделювання.

Експериментально-статистичний підхід дозволяє відволіктися від внутрішньої структури об’єкту та використати так званий принцип чорної скриньки, тобто вивчити залежність відгуку системи на зміну вхідних змінних.

Об’єкт дослідження можна зобразити наступним чином:

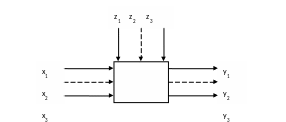
Фактори – вимірювані та регульовані вхідні змінні Х (незалежні змінні).

Перешкоди (збурення, шуми) – параметрі, що змінюються випадково, неконтрольовані параметри (стохастичні збурення), недоступні для вимірювання, проявляються втому, що змінюють дію факторів на вихідні змінні Y.

Вихідні змінні визначаються факторами і зв’язані з ціллю дослідження. Часто вихідні змінні називають параметрами оптимізації.

Результат експерименту називається випадковим, стохастичним, можливим або вирогідним. В результаті статистичного дослідження об’єкту математичний опис отримують у вигляді емпіричних залежностей, які зв’язують вихідні параметри об’єкту, що характеризують результат експерименту, з факторами.

y = f(x₁, x₂, ..., x₃);

Простір з координатами х₁, х₂, ..., х₃ прийнято називати факторним, графічне відображення функції відгуку у факторному просторі називають поверхнею відгуку.

4. Лінеаризувати задану статистичну характеристику C=f(G), задану таблицею:

G	1000	2000	3000	4000	5000	6000	7000	8000	10000
V	0.5	0.4	0.35	0.32	0.3	0.286	0.275	0.26	0.254

на відрізку [4000; 6000]

Якщо статична характеристика задана графічно або у вигляді статистичних даних і вона має ярко виражений нелінійний характер, проводять лінеаризацію на відрізку графічним методом у наступній послідовності:

• Проводимо дотичну до кривої через точку середини відрізку по аналогії до лінеаризації у точці;

• Через точки на кінцях відрізку проводимо стягуючу хорду;

• Результуюча характеристика проводиться по середині між хордою та дотичною;

Отже маємо: