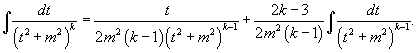1. Определение. Функция   называется первообразной функции  , если  .

         Теорема. Если   и   две первообразные одной и той же функции  , то  они отличаются не более, чем на константу, то есть  .

         Следствие. Если   - одна из первообразных функции  , то любая другая первообразная имеет вид  .

         Определение. Совокупность всех первообразных функции   называется неопределенным интегралом от   и обозначается  .

           называется подынтегральной функцией, а 

 - подынтегральным выражением.

         Таким образом, окончательно

.

         Свойства неопределенного интеграла.

         1.  ;

         2.  ;

         3.  ;

         4.  .

2. Методы интегрирования

Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:

F^' (x) = f(x).                                              (8.1)

Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -

∫ f(x) dx.

Если F(x) - какая-нибудь первобразная для функции f(x), то

∫ f(x)dx = F(x) + C,                                         (8.2)

где С - произвольная постоянная.

Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:

1) d ∫ f(x)=f(x)dx,

2) ∫df(x)=f(x)+C,

3) ∫af(x)dx=a ∫f(x)dx (a=const),

4) ∫(f(x)+g(x))dx= ∫f(x)dx+ ∫g(x)dx.

Список табличных интегралов

1. ∫x^ dx = x^+1/( + 1) +C; ( ≠ -1).

2. = ln x +C.

3. ∫ a^x dx = a^x/ln a + C (a>0, a ≠1).

4. ∫e^x dx = e^x + C.

5. ∫sin x dx = cos x + C.

6. ∫cos x dx = - sin x + C.

7.  = arctg x + C.

8.  = arcsin x + C.

9.  = tg x + C.

10.  = - ctg x + C.

Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.

Если функция f(z) непрерывна на [, ], функция z =g (x) имеет на [a,b] непрерывную производную и α ≤ g(x) ≤ β, то

∫ f(g(x)) g^' (x) dx = ∫f(z) dz,                                   (8.3)

причем после интегрирования в правой части следует сделать подстановку z=g(x).

Для доказательства достаточно записать исходный интеграл в виде:

∫ f(g(x)) g (x) dx = ∫ f(g(x)) dg(x).

Например:

1)  ;

2) .

Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные производные. Тогда, по правилу дифференцирования произведения,

d(uv)= udv + vdu или udv = d(uv) -vdu.

Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:

∫ udv = uv - ∫ vdu.                                                       (8.4)

Эта формула выражает правило интегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx.

Пусть, например, требуется найти x cosx dx. Положим u = x, dv = cos x dx, так что du=dx, v=sinx. Тогда

∫ x cos x dx = ∫ x d(sin x) = x sin x - ∫ sin x dx = x sin x + cos x + C.

Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,

∫ x^k ln^mx dx, ∫x^k sin bx dx, ∫ x^k cos bx dx, ∫x^k e ^ax dx

и другие, которые вычисляются именно с помощью интегрирования по частям.

Понятие определенного интеграла вводится следующим образом. Пусть на отрезке [a, b] определена функция f(x). Разобьем отрезок [a,b] на n частей точками a = x₀ < x₁ <...<x_n = b. Из каждого интервала (x_i-1, x_i) возьмем произвольную точку _i и составим сумму  f(_i)Δ x_i, где Δx_i = x_i - x_i1. Сумма вида  f(_i)Δ x_i называется интегральной суммой, а ее предел при λ = max Δx_i→ 0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:

  f(_i)Δ x_i.                                          (8.5)

Функция f(x) в этом случае называется интегрируемой на отрезке [a, b], числа a и b носят название нижнего и верхнего предела интеграла.

Для определенного интеграла справедливы следующие свойства:

1)  ;

2)  ;

3)  -  ;

4)  , (k = const, k∈R);

5)  ;

6)  ;

7)   f(ξ)(b-a) (ξ∈a,b]).

Последнее свойство называется теоремой о среднем значении.

Пусть f(x) непрерывна на [a, b]. Тогда на этом отрезке существует неопределенный интеграл

∫f(x) dx = F(x) + C

и имеет место формула Ньютона-Лейбница, cвязывающая определенный интеграл с неопределенным:

 F(b) - F(a).                                                (8.6)

Геометрическая интерпретация: определенный интеграл   представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x = b и отрезком оси Ox.

Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода - это интегралы на бесконечном промежутке, определяемые следующим образом:

.                                           (8.7)

Если этот предел существует и конечен, то   называется сходящимся несобственным интегралом от f(x) на интервале [а,+ ∞), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+ ∞). В противном случае про интеграл   говорят, что он не существует, или расходится.

Аналогично определяются несобственные интегралы на интервалах (- ∞, b] и (- ∞, + ∞):

.

Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка [a,b], кроме точки с, вкоторой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:

,

если эти пределы существуют и конечны. Обозначение:

 =  .                               (8.8)

Таблица основных интегралов

Замена переменных.

Пусть надо вычислить  . Сделаем замену переменных  , так что  . Пусть нам каким-то образом удалось вычислить  . Тогда имеет место формула

.

         Интегрирование по частям.

         Пусть   и   - две функции. Тогда имеет место формула

.

Заменой переменной неопределенного интеграла.

При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.

ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t [α,β].

Тогда справедливо следующее равенство:

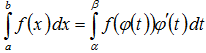
Эта формула носит название формулы замены переменной в определенном интеграле.

Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).

3. Интегрирование рациональных дробей.

 

Теорема 6. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором ее знаменатель не равен нулю, существует и выражается через элементарные функции, а именно рациональные дроби, логарифмы и арктангенсы.

Доказательство.

Представим рациональную дробь   в виде:   . При этом последнее слагаемое является правильной дробью, и по теореме 5 ее можно представить в виде линейной комбинации простейших дробей.  Таким образом, интегрирование рациональной дроби сводится к интегрированию многочлена S(x) и простейших дробей, первообразные которых, как было показано, имеют вид, указанный в теореме.

 

Замечание. Основную трудность при этом составляет разложение знаменателя на множители, то есть поиск всех его корней.

 

Интегрирование рациональных функций

Для интегрирования рациональной функции  , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов: Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение; Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений; Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов; Вычислить интегралы от простейших дробей. Шаг 1. Преобразование неправильной рациональной дроби Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочленP(x) на Q(x). Получим следующее выражение: где   - правильная рациональная дробь.  Шаг 2. Разложение знаменателя на простейшие дроби Запишем многочлен знаменателя Q(x) в виде где квадратичные функции являются несократимыми, то есть не имеющими действительных корней.  Шаг 3. Разложение рациональной дроби на сумму простейших дробей. Запишем рациональную функцию в следующем виде: Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x).  Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.  Шаг 4. Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул: У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат: где   Затем применяются следующие формулы: Интеграл   может быть вычислен за k шагов с помощью формулы редукции

4. Интегрирование некоторых тригонометрических функций

В данном разделе мы рассмотрим 8 специальных классов интегралов от тригонометрических функций. Для каждого класса применяются определенные преобразования и подстановки, позволяющие получить аналитическое решение.  1. Интегралы вида  Для решения данных интегралов применяются формулы преобразования произведения тригонометрические функций в сумму или разность: 2. Интегралы вида  Здесь и везде ниже предполагается, что m и n - натуральные числа. Для вычисления таких интегралов используются следующие подстановки и преобразования: Если степень косинуса n - нечетная (при этом степень синуса m может быть любой), то используется подстановка  . Если степень синуса m - нечетная, то используется подстановка  . Если степени m и n - четные, то сначала применяются формулы двойного угла чтобы понизить синуса или косинуса в подынтегральном выражении. Затем, если необходимо, применяются правила a) или b). 3. Интегралы вида  Степень подынтегрального выражения в данном интеграле можно понизить с помошью тригонометрического соотношения   и формулы редукции 4. Интегралы вида  Здесь степень подынтегрального выражения понижается с помошью соотношения   и формулы редукции 5. Интегралы вида  Данный тип интеграла упрощается с помощью следующей формулы редукции: 6. Интегралы вида  Аналогично предыдущим пунктам, интеграл упрощается с помощью формулы 7. Интегралы вида  Если степень секанса n - четная, то c помошью соотношения   секанс выражается через тангенс. При этом множитель   отделяется и используется для преобразования дифференциала. В результате весь интеграл (включая дифференциал) выражается через функцию tg x. Если обе степени n и m - нечетные, то отделяется множитель sec x tg x, необходимый для преобразования дифференциала. Далее весь интеграл выражается через sec x. Если степень секанса n - нечетная, а степень тангенса m - четная, то тангенс выражается через секанс с помощью формулы  . Затем вычисляются интегралы от секанса. 8. Интегралы вида  Если степень косеканса n - четная, то c помошью соотношения   косеканс выражается через котангенс. При этом множитель   отделяется и используется для преобразования дифференциала. В результате подынтегральная функция и дифференциал выражаются через ctg x. Если обе степени n и m - нечетные, то отделяется множитель ctg x cosec x, необходимый для преобразования дифференциала. Далее интеграл выражается через cosec x. Если степень косеканса n - нечетная, а степень котангенса m - четная, то котангенс выражается через косеканс с помощью формулы  . Далее вычисляются интегралы от косеканса.