
- •Джиргалова с.Б., Киреева о.В., Тугульчиева в.С.
- •Лабораторная работа №1 Первообразная. Неопределенный интеграл.
- •Лабораторная работа №2 Методы интегрирования (Замена переменной. Интегрирование по частям.)
- •Замена переменной.
- •Интегрирование по частям.
- •1)Обычно в интегралах вида
- •3) Интегралы вида
- •Варианты
- •Лабораторная работа №3 Интегрирование рациональных выражений. Метод неопределенных коэффициентов.
- •Лабораторная работа № 4 Интегрирование рациональных дробей. Метод Остроградского.
- •1. В чем заключается метод Остроградского и когда им пользуются? лабораторная работа №5 Интегрирование тригонометрических функций.
- •Варианты
- •Лабораторная работа №6 Интегрирование некоторых выражений, содержащих радикалы
- •Интегрирование выражений вида
- •Интегрирование биноминальных дифференциалов.
- •III. Интегрирование выражений вида . Подстановки Эйлера.
- •Лабораторная работа №7 Определенный интеграл. Свойства определенного интеграла. Вычисление определенных интегралов.
- •Варианты
- •Лабораторная работа №8. Замена переменной в определенном интеграле и интегрирование по частям.
- •Интегрирование по частям в определенном интеграле.
- •Варианты
- •Лабораторная работа №9. Геометрические приложения определенного интеграла . Площадь плоской фигуры.
- •Лабораторная работа №10 Геометрические приложения определенного интеграла. Длина дуги кривой.
- •Литература:
Варианты
Вычислить интегралы: 1) – с помощью предельного перехода от интегральных сумм;
2)-7) по формуле Ньютона – Лейбница.
В-1
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
 6)
6)
![]()
7)
![]()
В-2
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)![]()
В-3
1)
![]() 2)
2)
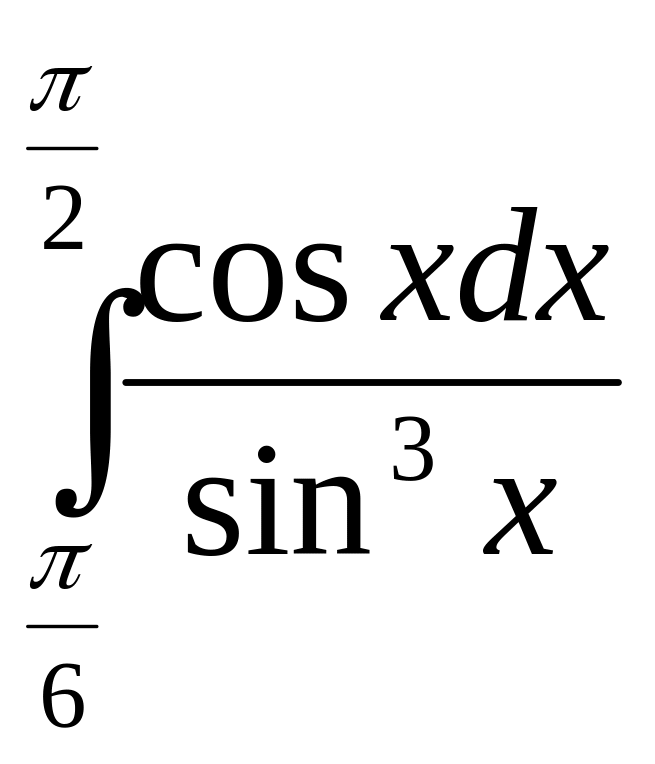 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]()
В-4
1)
![]() 2)
2)
![]() 3)
3)
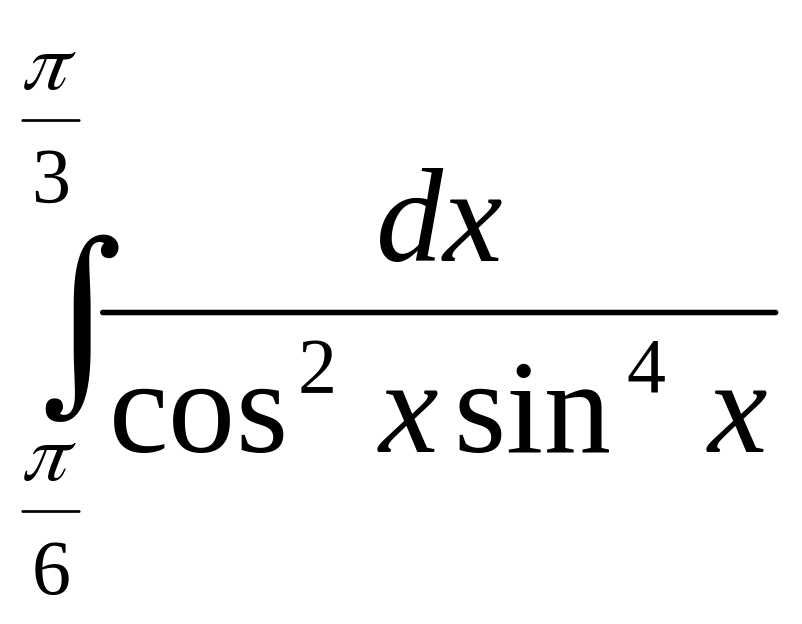
4)
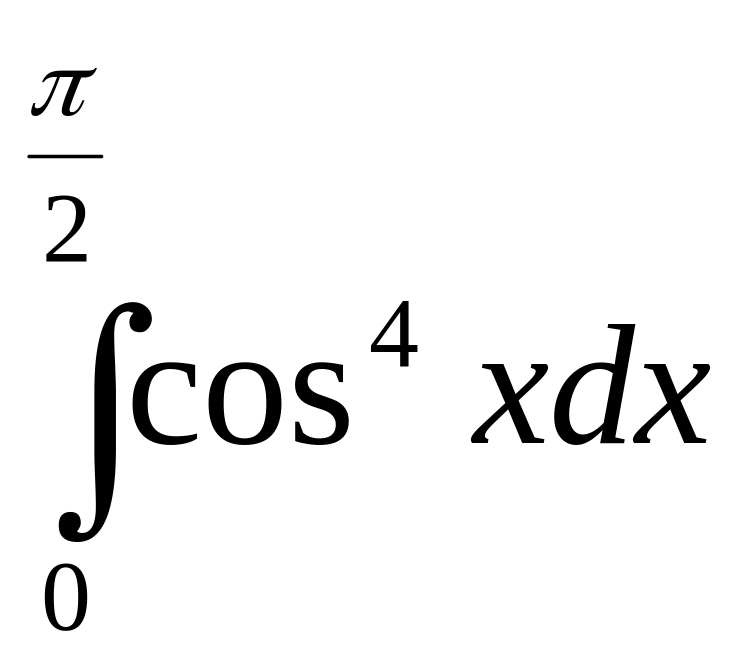 5)
5)
![]() 6)
6)
![]()
7)

В-5
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
 6)
6)
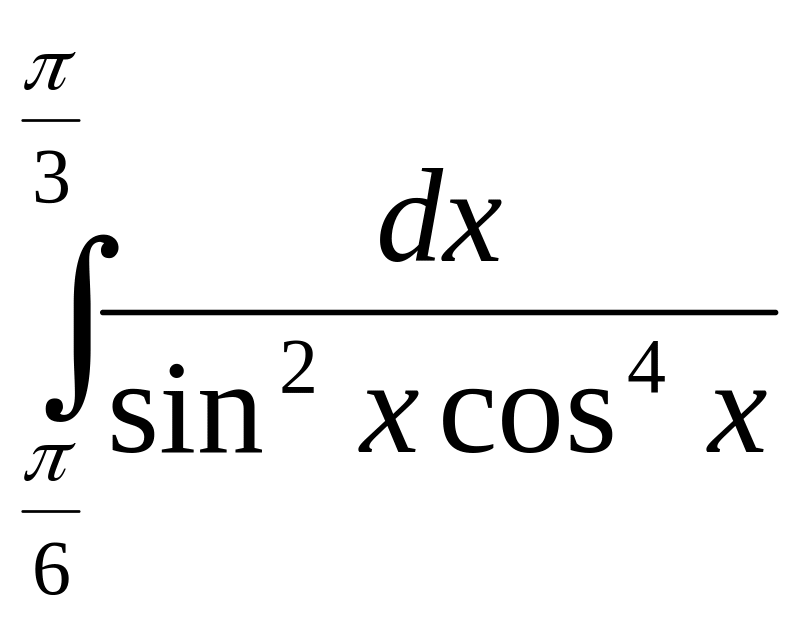
7)
![]()
В-6
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
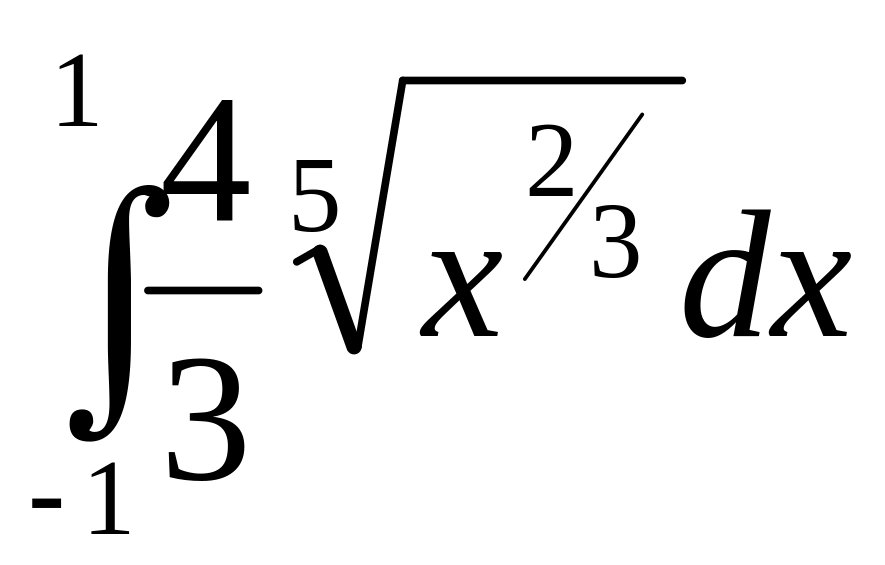 5)
5)
 6)
6)
![]()
7)
![]()
В-7
1)
![]() 2)
2)
![]() 3)
3)
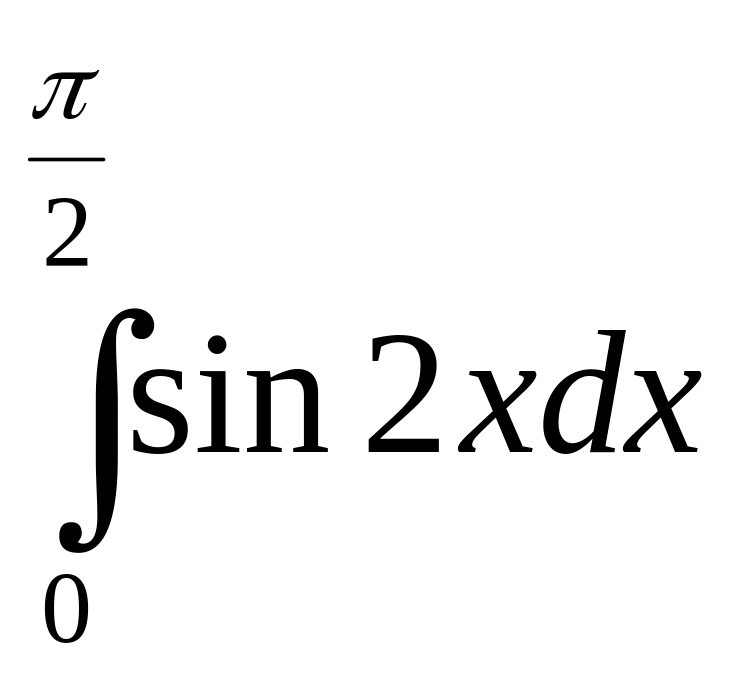
4)
![]() 5)
5)
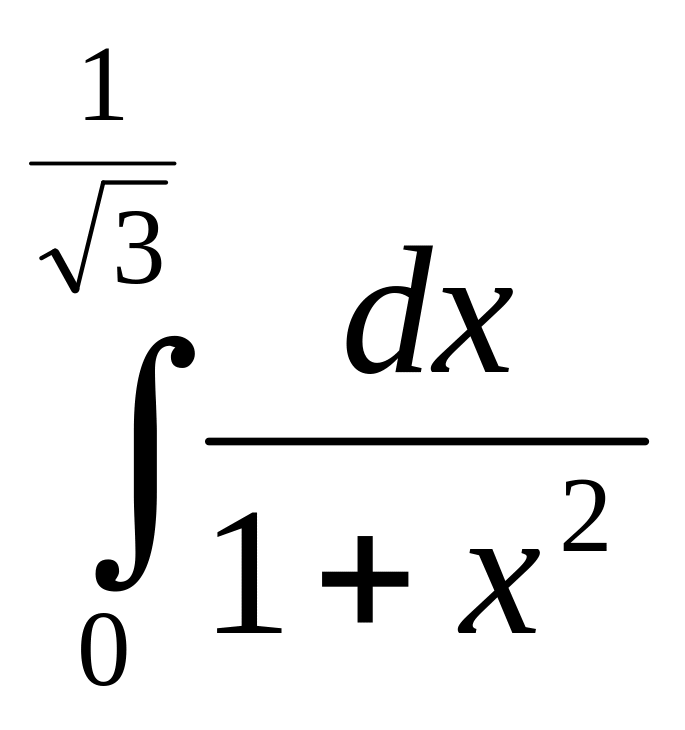 6)
6)
![]()
7)
![]()
В-8
1)![]() 2)
2)
![]() 3)
3)
4)
![]() 5)
5)
![]() 6)
6)
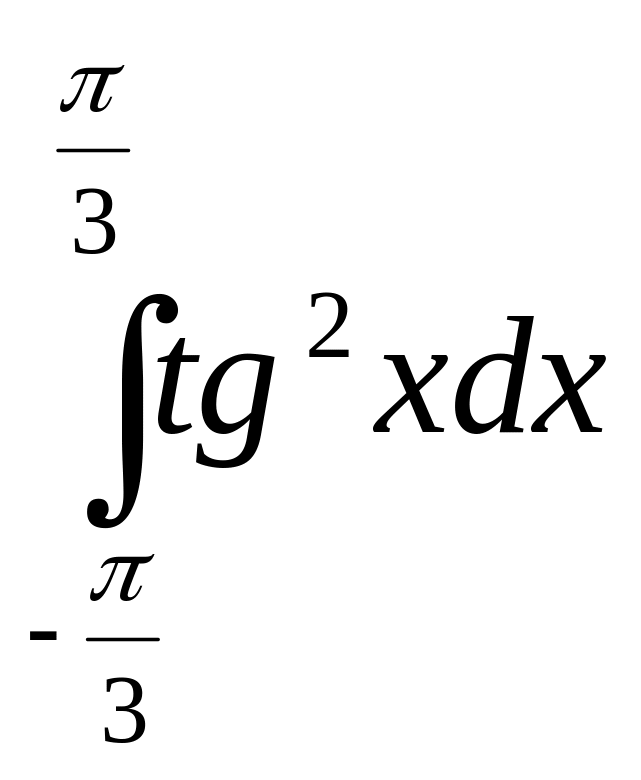
7)
![]()
В-9
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
 5)
5)
![]() 6)
6)
![]()
7)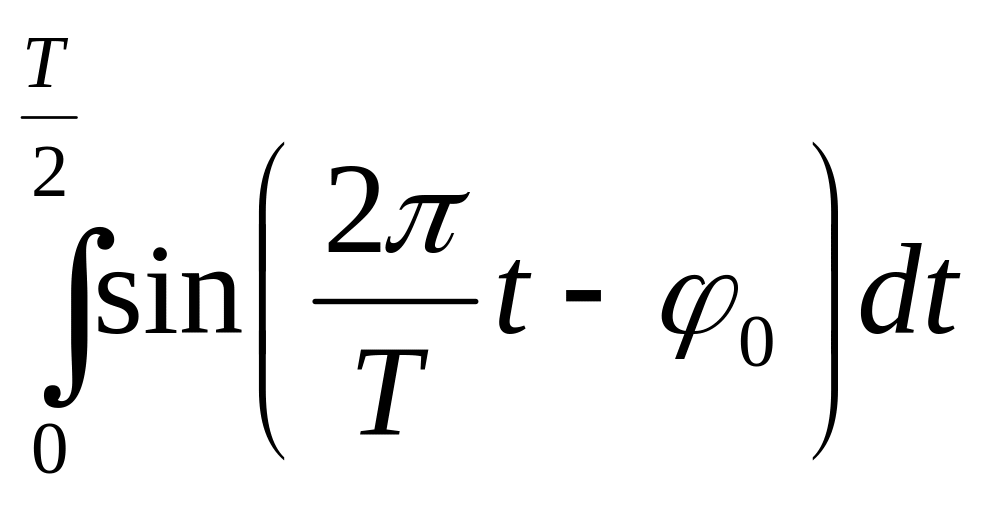
В-10
1)
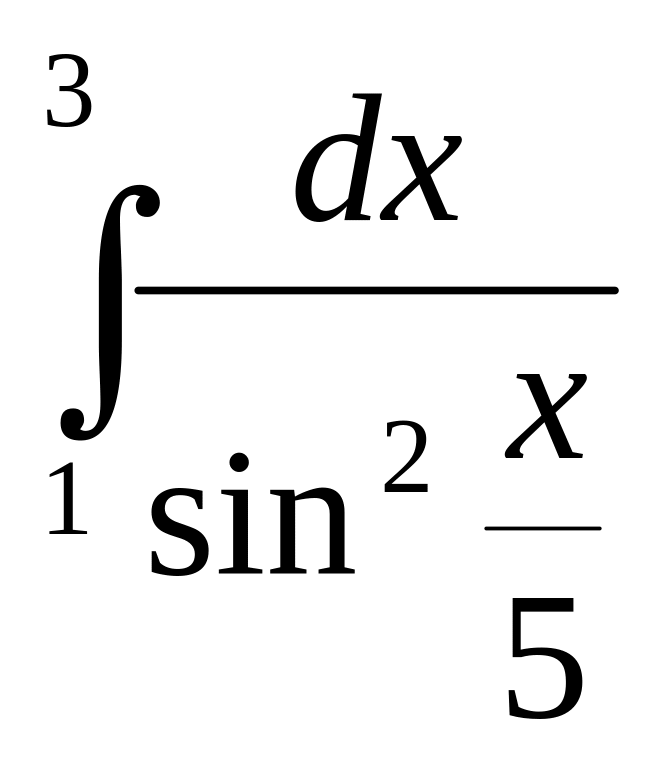 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]()
В-11
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
 6)
6)![]()
7)
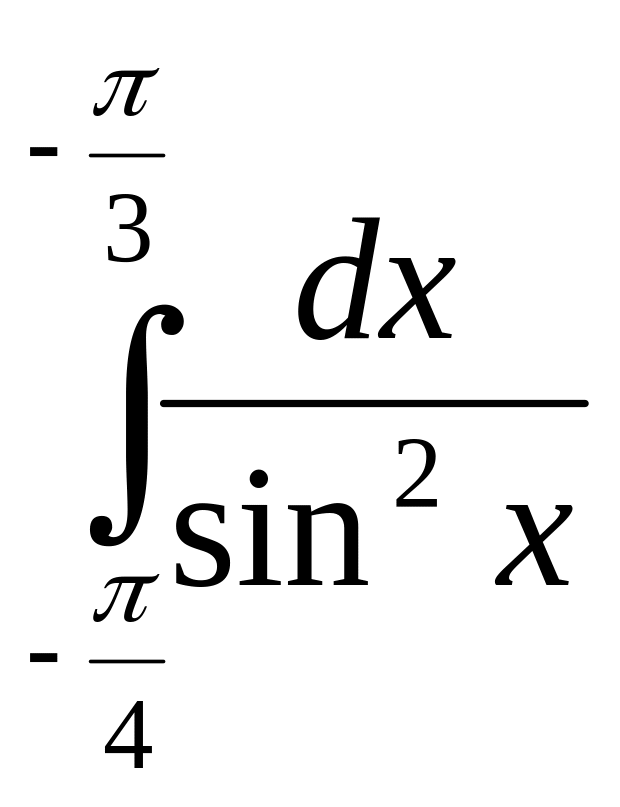
В-12
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
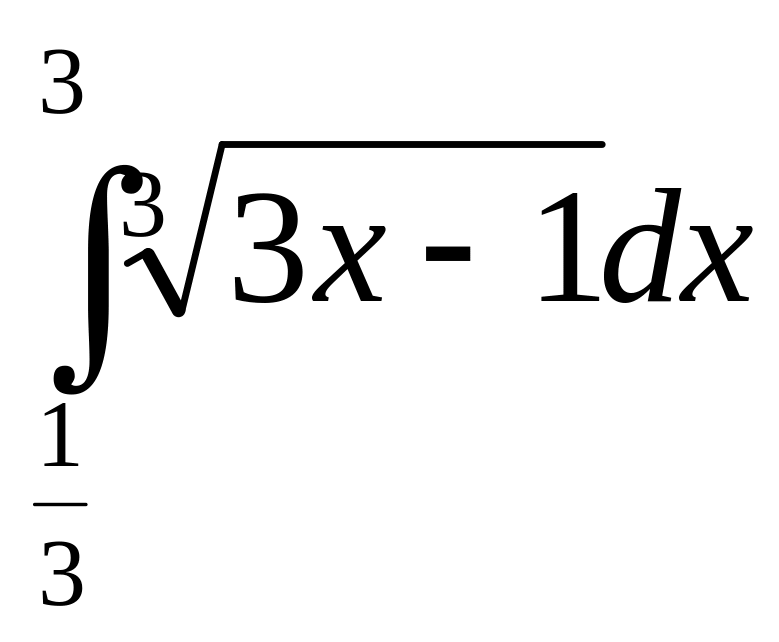 6)
6)

7)
![]()
В-13
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
5)![]() 6)
6)

7)
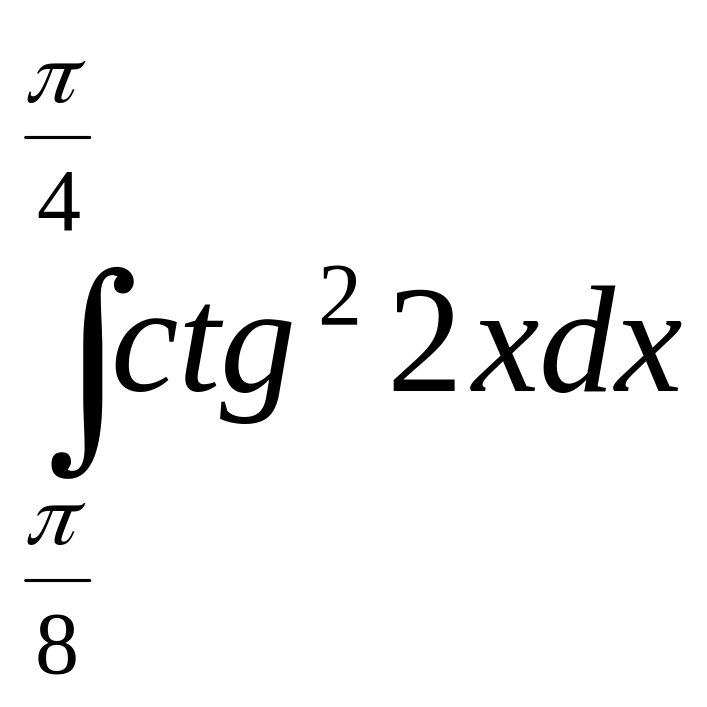
В-14
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
 5)
5)
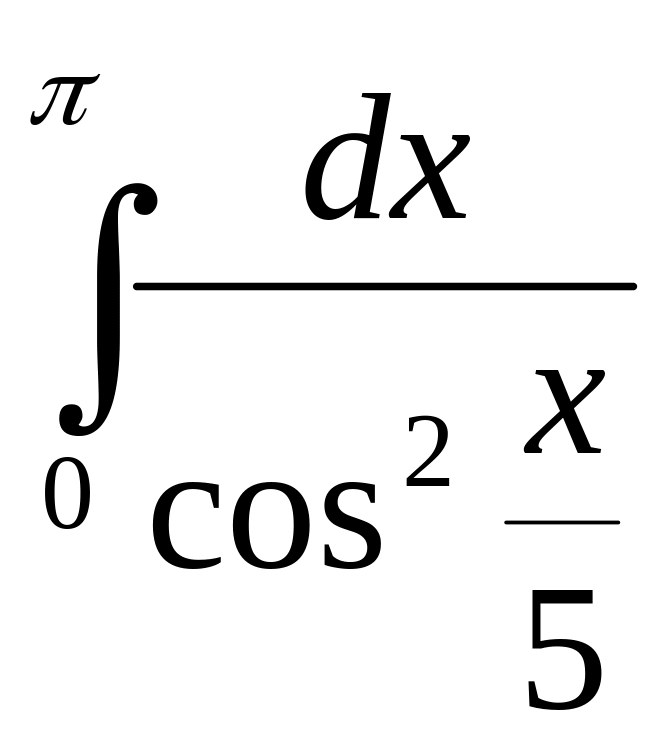 6)
6)
![]()
7)
![]()
В-15
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
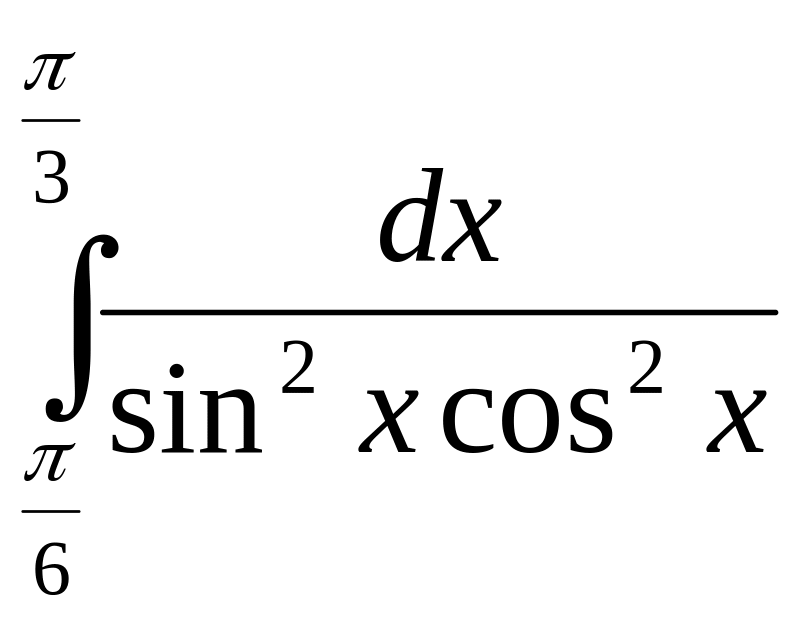
В-16
1)
![]() 2)
2)
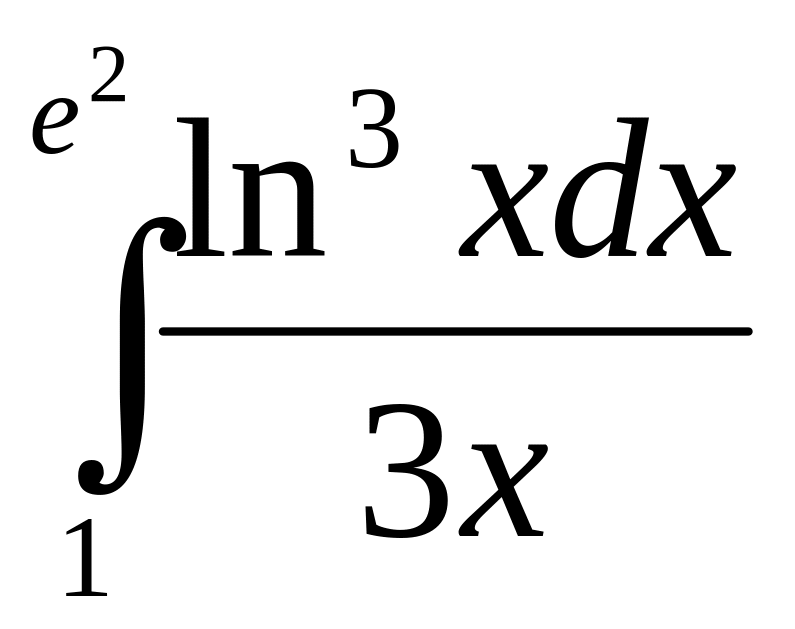 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)

В-17
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]()
В-18
1)
 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]()
В-19
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
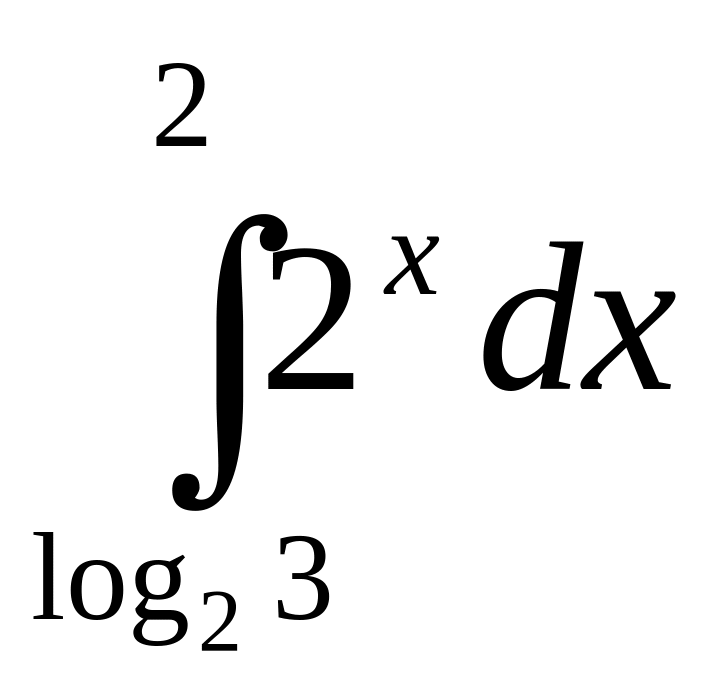
В-20
1) 2)
2)![]() 3)
3)
![]()
4)
![]() 5)
5)![]() 6)
6)
![]()
7)
![]()
В-21
1)
![]() 2)
2)
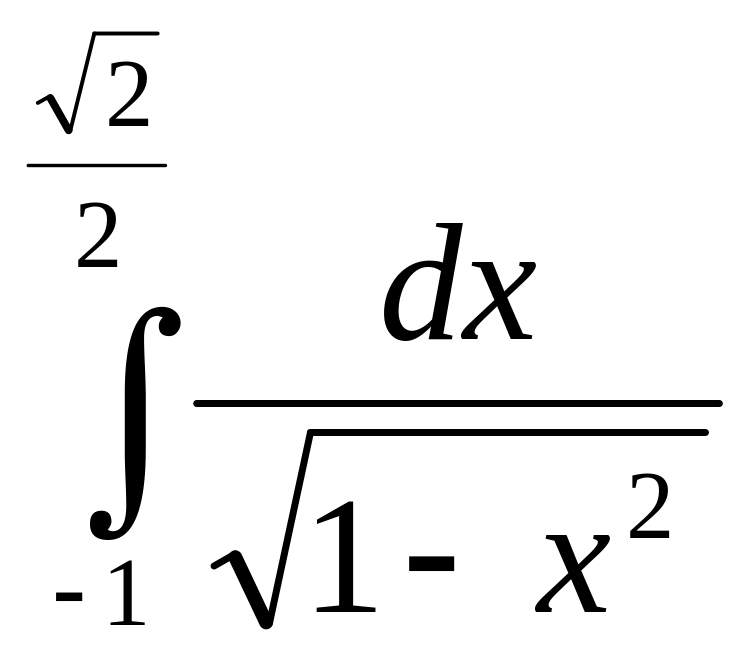 3)
3)
4)
![]() 5)
5)
![]() 6)
6)
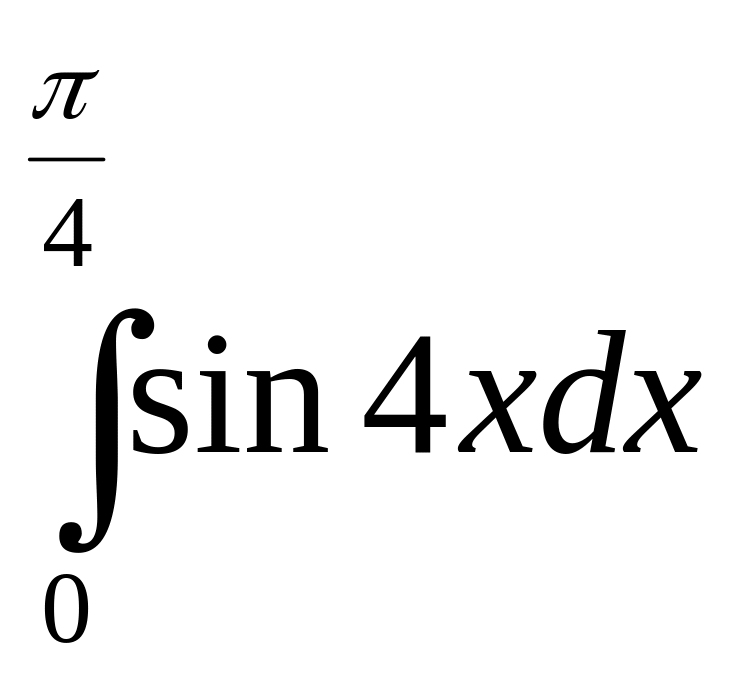
7)
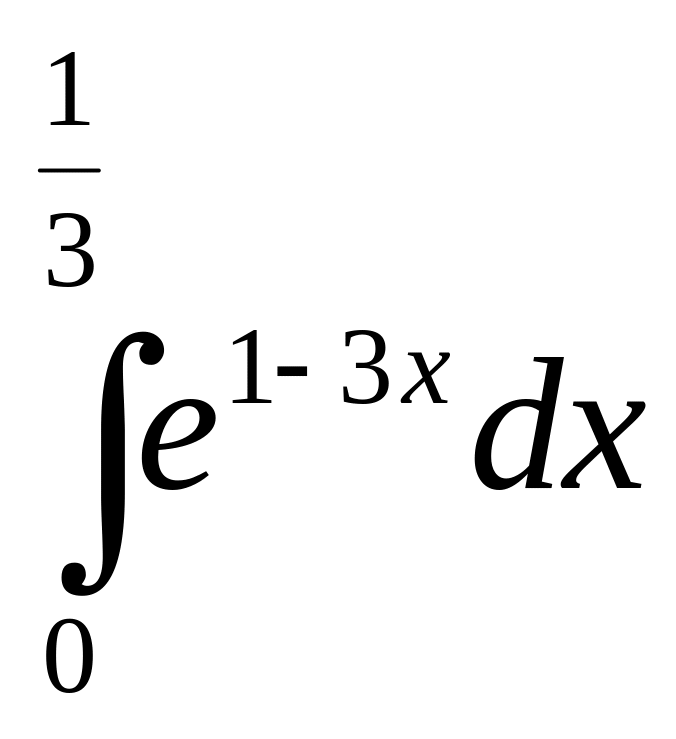
В-22
1)
![]() 2)
2)
 3)
3)
![]()
4)
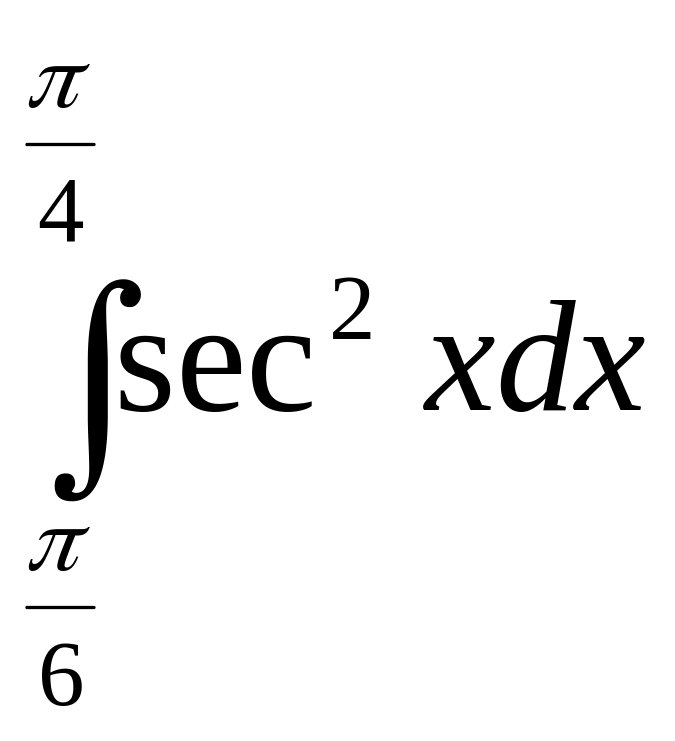 5)
5)
![]() 6)
6)
![]()
7)
![]()
В-23
1)
![]() 2)
2)
 3)
3)
![]()
4)
5)
![]() 6)
6)
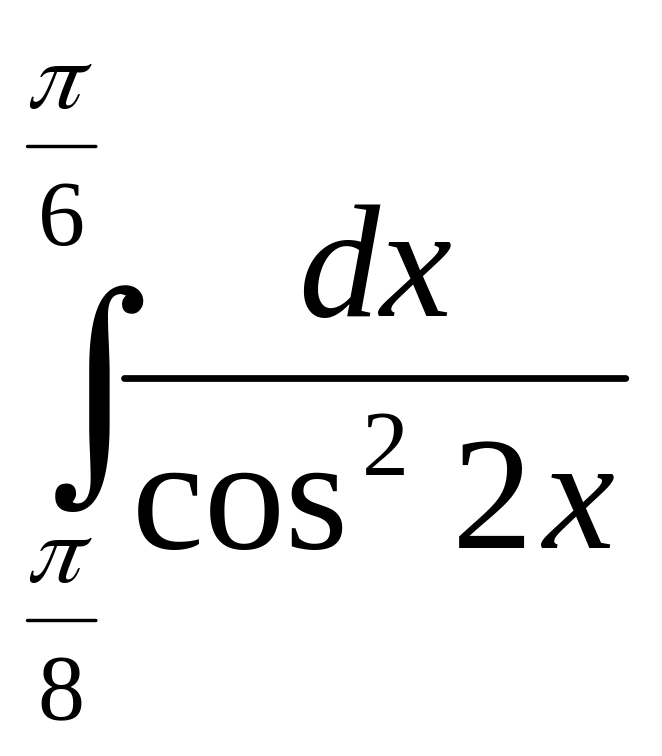
7)

В-24
1)
![]() 2)
2)
 3)
3)
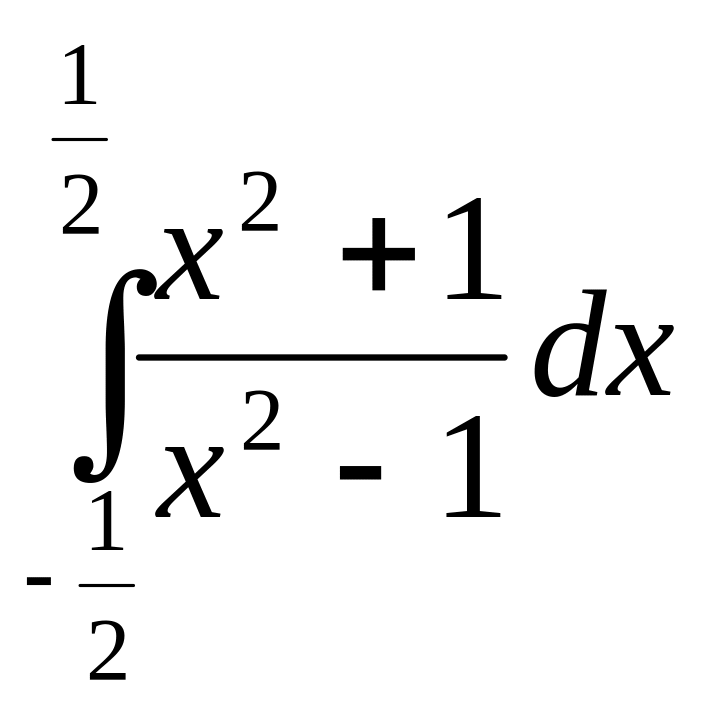
4)
![]() 5)
5)
![]() 6)
6)

7)
![]()
В-25
 2)
2)
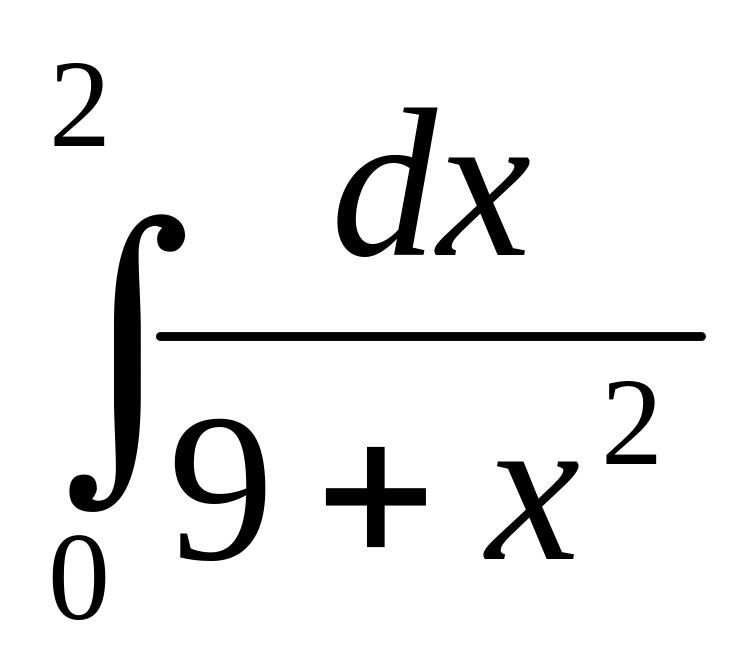 3)
3)

4)
![]() 5)
6)
5)
6)

7)
![]()
Вопросы к лабораторной работе №7:
Что называется определенным интегралом от функции на отрезке ?
Зависит ли величина определенного интеграла от способа разбиения ? А от выбора промежуточного значения точек ?
Каков геометрический смысл интегральной суммы определенного интеграла?
Укажите необходимое условие интегрируемости функции.
Как составляются суммы Дарбу? Какими свойствами они обладают?
Как связаны суммы Дарбу с интегральными суммами при фиксированном разбиении?
Каковы основные свойства определенных интегралов?
Сформулируйте и докажите теорему о среднем. Каков ее геометрический смысл?
Используя теорему о среднем, докажите непрерывность определенного интеграла с переменным верхним пределом как функции верхнего предела.
Известно, что непрерывная в данном промежутке функция всегда имеет в нем первообразную. Из какого свойства определенного интеграла это следует?
