Лабораторная работа №5 / лаба по Тау5

Санкт-Петербургский Государственный Электротехнический Университет.

Отчет к Лабораторной работе №5 по ТАУ.

«Изучение методов построения фазовых портретов нелинейных динамических систем»

Выполнили:

гр.1321

Волох К.А.

Петренко В.

Санкт-Петербург 2004г.

Цель работы: Построение фазовых характеристик динамических систем.

Пример1:

l – длина маятника.

Маятник, отклоненный от нижнего положения равновесия на угол Θ.

ДУ:

Точки равновесия: 0, ±π, ±2π.

Линеаризованное уравнение для малых отклонений от положения равновесия дифференциального уравнения имеют вид:

Л.У: - четные

- нечетные

Теперь характеристические полиномы линеаризованных уравнений:

s²+; s²- имеют корни s_1,2=±j√(g/l); s_1,2=±√(g/l);

В окрестности нижних положений равновесия («четных») фазовые портреты типа центр, а в окрестности верхних («нечетных») – седло.

Для больших отклонений от положения равновесия фазовой траектории будем строить численным методом с помощью программы MatLab Simulink.

Уравнение в форме Коши:

Поделим первое уравнение на второе.

Разрешим это уравнение, с помощью интегрирования переменных

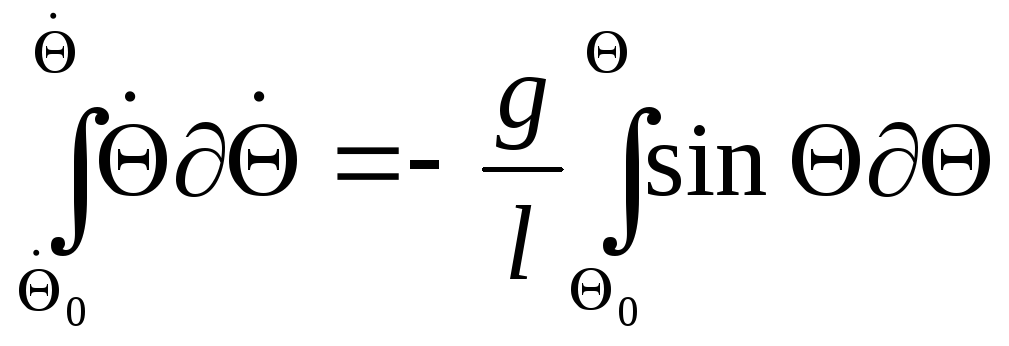
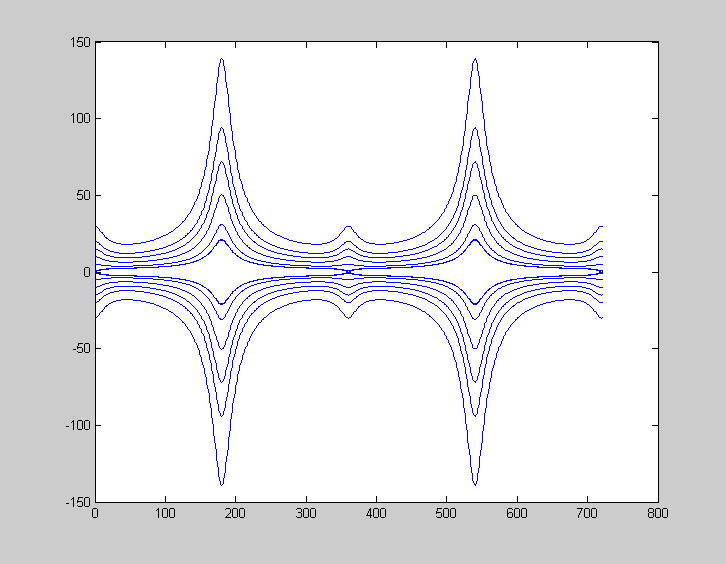
При начальном отклонении маятника на 1 рад, получим следующую зависимость.

Начальное угловое ускорение равно 0.1 рад/с

=

phase1.m

//------------------------

function phase()

mas(722)=0;

for i=1:361*2 // i - градусы

n=i*(2*pi/360);

mas(i)=sqrt(19.62*cos(n)-0.01-19.62*0.54);

end

plot(abs(mas))

hold

plot(-abs(mas))

//------------------------

>>phase1

Пример2: Маятник на каретке.

Исходные уравнения системы:

В форме Коши уравнение примет вид:

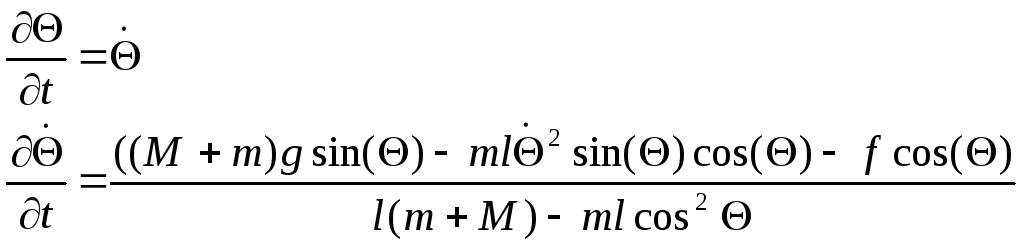
Поделим первое уравнение на второе.

Для больших углов отклонения интегрирование полученного уравнения затруднено, поэтому проведем относительное интегрирование.

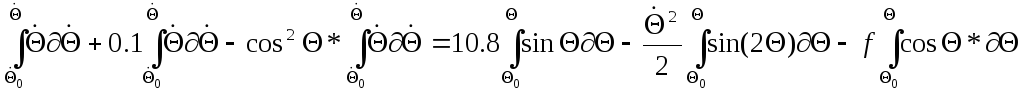
Проекция фазовой траектории на плоскость (,)

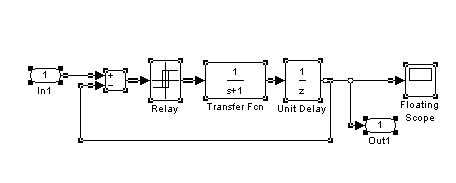
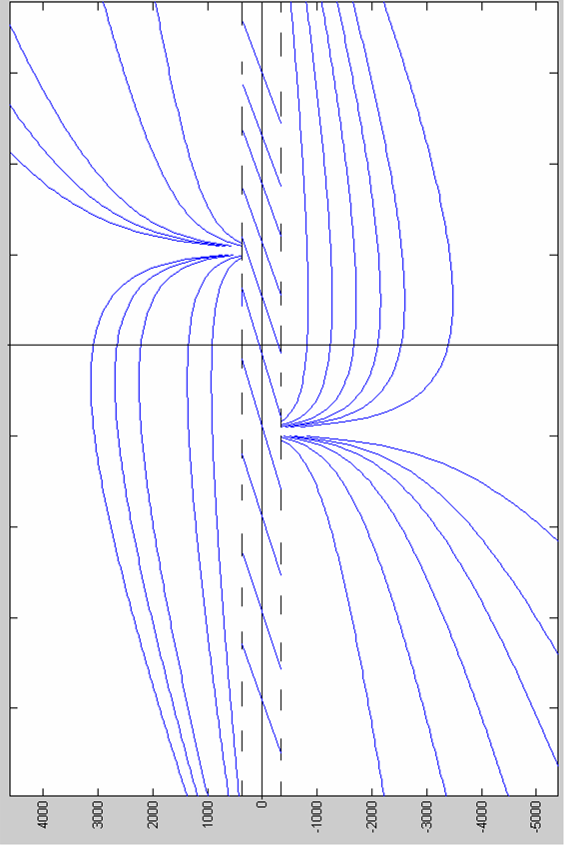
Пример3: Релейная система управления.

Фазовый портрет на плоскость(,)

=

x y

Модель представлена в форме структурной схемы. Запишем модель в форме 2-х уравнений 1-го порядка.

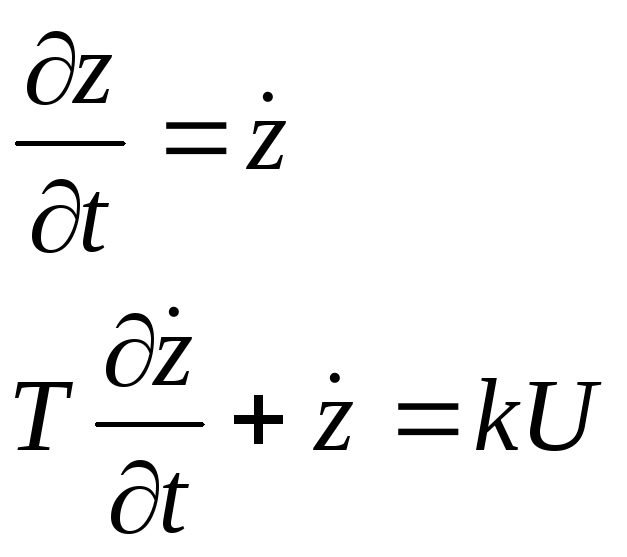
x=-z элемент сравнения. Выберем следующие элементы состояния(x,)

y=F(x)

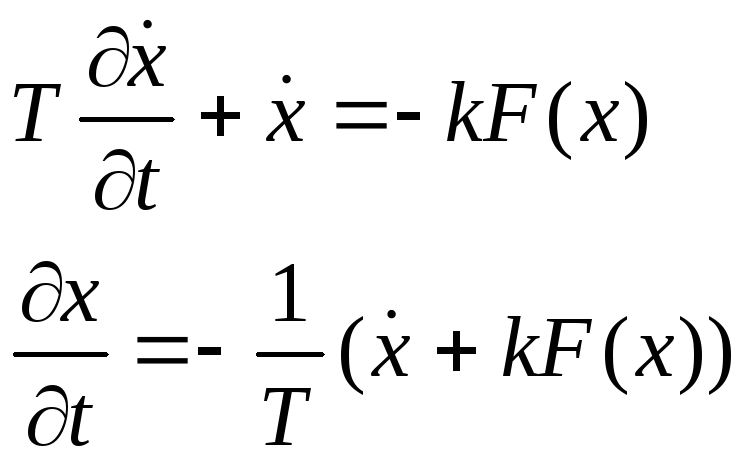
Получим:

Найдем положение равновесия:

Нет изолированных особых точек, поэтому не можем воспользоваться малой линеаризацией для малых отклонений.

Учтем, что F(x) – кусочно-постоянная функция.

Разделим переменные.

3 уравнения фазовых траекторий по участкам:

1. x>b; F(x)=+C:

2. |x|<=b; F(x)=0:

3. x<-b; F(x)=-C

Пример4: Модель Рёсслера «Спиральный хаос»

Проекция на плоскость (x,y)

Поделим второе уравнение на второе:

;

Поделим первое на второе:

;

;

Интегрирование дает следующие результаты:

xz+0.32yz=0.3xy+2.25x²+1.44yx+2.25y²-(1/3)x³-0.16yx²-0.5xy²;

=Z

Интегрирование дает следующую зависимость: