19. Полигон и гистограмма.

Полигоном частот наз. ломаную, отрезки кот. соединяют точки c координатами: 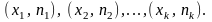Для изуч-я непрер. признака строится гистограмма. Для этого инт-л [a,b], где 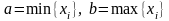, делится на неск. частичных инт-лов одинак. длины h. Затем подсчитыв-ся число вариант n_i, попавших в каждый инт-л.

Гистограмма–фигура, состоящая из прямоуг., основанием кот. служат частичн. инт-лы длины h, а высоты n_i/h.

Тогда площадь i-го прямоуг. равна 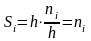, а площадь всей гистограммы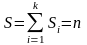 , где n-объем выборки.

Аналогично строится гистограмма относит. частот. При этом вдоль оси Oy откладыв-ся w_i/h. Тогда площадь i-го прямоуг. равна 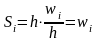.А площадь всей гистограммы .

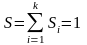Аналогичным св-вом нормировки обладает плотность распр. вер-тей. Т.обр., гистограмма служит для оценки вида плотности вер-ти.

20. Числовые характеристики выборки.

Выбор. ср. наз. ср. арифм. знач-е вариант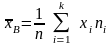

Выбор. дисперсией наз. ср. знач-е квадратов отклон-я вариант от среднего.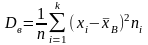

Если раскрыть скобки, получим еще одну формулу для вычисл. дисп.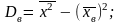

Выбор. ср. квадрат. отклон. наз. корень квадр. из дисп.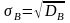 . Размах варьиров. .

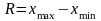Нач. моментом r-го порядка наз. ср. знач-е r-ых степеней вариант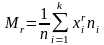

Центр. моментом r-го порядка наз. ср. знач-е отклонений в степени r от среднего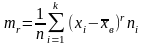

Асиметрией наз. величину равную .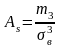

Пределы значений асимметрии от -∞ до +∞. При Ai=0 распр-е симметрично, в частности для норм. распр. Ai=0

Эксцессом наз. величину равную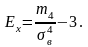

Эксцесс показыв. степень крутости кривой распр. признака Х по сравнению с крутостью норм. распр. Значения эксцесса лежат в полуинт-ле [-3;+ ∞) Для норм. распр. .

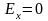21. Точечное оценивание.

Стат. оценкой наз. люб. ф-я выборк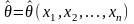

Точечн. оценкой наз. оценка, кот. дается одним числом.

Для того, чтобы стат. оценка давала хорошее приближение оцениваемому пар-ру θ, она д. обладать определен. св-вами. Оценка 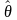наз. несмещен., если ее мат. ожид. равно оцениваемому пар-ру 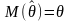.Это св-во означ. отсутствие ошибки одного знака. Примером несмещен. оценки явл. выбор. ср. для мат. ожид. Докажем. Выбор. знач-я xi м. рассматрив. как независ. случ. величины, взятые из одного и того же распределения. Пусть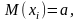 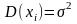. 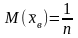.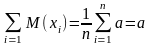Примером смещен. оценки явл. выбор. дисп. для теорет. дисп. М. показать, что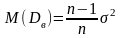 . Для того, чтобы получ. несмещен. Оценку σ², вводится понятие исправлен. выбор. дисп.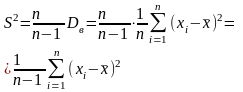 . 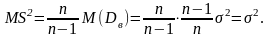Оценка пар-ра θ наз. состоятельн., если для люб. 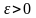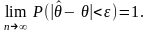Состоятельность оценки означ., что при больш. объеме выборки оценка приближ-ся к истин. знач-ю пар-ра θ (чем больше n, тем точнее оценка). Оценки, облад. св-вом несмещенности и состоят-ти, при ограничен. объеме выборки м. отличатся дисперсиями. Чем меньше дисп. оценки, тем меньше вер-ть ошибки при вычислении . Поэтому целесообразно, чтобы дисп. оценки была миним., т.е. чтобы выполнялось усл-е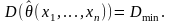 Оценка, обладающая таким св-вом, наз. эффективной.

22. Доверительные интервалы.

Оценка неизвестн. пар-ра, кот. задается 2 числами (концами инт-ла) наз. интервальной. Пусть по выборке получена точечн. оценка неизвестн. пар-ра 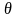. Эта оценка тем точнее, чем меньше 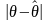. Пусть 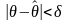, где 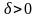. Методы мат. стат. не позвол. на 100% утвержд., что выполн-ся это нер-во. М. лишь говор. о вер-ти его выполн-я .

Величина γ—наз. доверит. вер-тью/надежностью. В кач-ве γ берут число близкое к единице. Оно выбир-ся исследователем самостоятельно. Раскрыв знак модуля получим определение доверит. инт-ла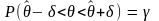

Доверит. наз. инт-л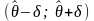 ,кот. покрыв. неизвестн. пар-р θ с задан. надежностью γ. При этом δ наз. точностью оценки. Замечание. Неверно говор., что θ попадает в инт-л. Задача состоит в том, чтобы построить такой инт-л, кот. бы заключал в себе θ. Доверит. инт-лы строятся след. образом: 1)вычисл-ся точечн. оценка , 2)выбир-ся надежность γ,3)вычисл-ся точность оценки δ.