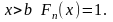15. Закон больших чисел (збч).

(ЗБЧ) показ., что ср. результат при дост. большом кол-ве испытаний утрачивает случайный

хар-р и может быть предсказан с дост. точностью.

Нерав-во Чебышева. Сходимость случ. послед-тей

Если случ. величина Х имеет мат. ожид. МХ=а и дисп. DX, то для люб. ε>0 справ-во нер-во Чебышева:

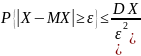. Нер-во Ч. м. записать в др. форме:

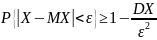
Во 2-ой формуле оно устанавлив. ижн. границу вер-ти события, в 1-ой—верхнюю.

Нер-во Ч. справ-во для люб. случ. величин. В частности, для случ. величин X=m, имеющей биномин. Распр. с мат. ожид. МХ=а=np и дисп. DX=npq, оно принимает вид

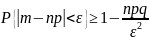
Для частости m/n события в nнезавис. Испытаниях, в каждом из кот. оно м. произойти с вер-тью р=М(m/n)=а, дисп. кот. D(m/n)=pq/n, нер-во Ч. им. вид

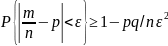
Суть закона больших чисел: если число случайных величин неограниченно растет, то их среднее арифметическое утрачивает смысл случайной величины и стремится к постоянной величине, равной среднему арифметическому их математических

ожиданий:

 > - стрелочка.

16. Центральная предельная теорема.

Многие задачи ТВ связ. с изуч-ем суммы независ. случ. величин, кот. при определен. усл-ях им. распред-е, близкое к норм. Эти усл-я выраж-ся центр. пред. теоремой(ЦПТ). Пусть ₁, ₂,…, _n,…– послед-ть независ. случ. величин. Обозначим η_n= ₁ + ₂ +…+ _n . Говорят, что к послед-ти ₁, ₂,…, _n,… применима ЦПТ, если при n→∞ закон распр. η_n стремится к норм.:

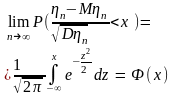
Суть ЦПТ: при неограничен. увеличении числа случ. величин закон распр. суммы стремится к норм.

Частным случаем ЦТП явл. интегр. пред. теорема Муавра-Лапласа .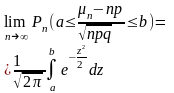

Док-во: Ранее показано, что Мμ_n=np, Dμ =npq. Пусть a=-∞, b=x, тогда

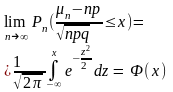
Сформулир. ЦПТ для одинаково распределен. cлуч. величин: Теорема: Пусть с.в. ₁, ₂,…, _n ,… независимы, одинаково распределены, им. конечные мат. ожид. 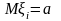и дисп. 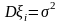. Тогда к этой последов-ти применима ЦТП:

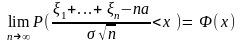
17. Выборочный метод.

Сов-ть объектов, взятых для исслед-я, назыв. выборкой. Сов-ть объектов, из кот. взята выборка, наз. генеральной. Число объектов сов-ти наз. объемом.

Чтобы выборка хорошо отражала генер. сов-ть, она д.б. случ. и выбор. знач-я д.б. независимыми. Перечень вариантов, записан. в возрастающем порядке и соответствующих частот (относит. частот), наз. стат. распред-ем выборки или вариац. рядом.

Относит. частотами наз. отнош-е частоты к объему выборки:

.

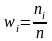18. Эмпирическая функция распределения.

Эмпирич. ф-цией распр. наз. ф-я, определяющая для каждого знач-я x относит. частоту события (X<x)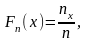

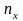- число вариант меньших x, n- объем выборки.

В теории вер-тей F(x) определяет вер-ть события (X<x). На основании теоремы Бернулли при 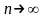эмпирич. ф-я распр. стрем-ся к теорет.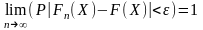

Т.обр., эмпир. ф-я распр. строится для оценки вида теорет. ф-ции определения.

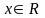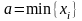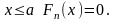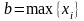Св-ва: 1)Для люб. x ф-ция распр. заключена в инт-ле от 0 до 1: 0≤F(x)≤1. 2)F(x)–неубывающая ф-я. 3)F(x) непрер. слева в каждой точке . 4)Если , то для каждого Если , то для каждого