1.Случайные события. Действия над ними

Пусть в рез-те испытания един-но возможно появл-е n несовместн. равновероятн. событий E₁, E₂,…, E_n. Такие события элементарные. Понятие равновер-ти явл. неопределяемым в теории вер-тей и счит-ся интуитивно ясным. Напр., при подбрас-нии монетки равновероятно выпадение люб. стороны. Несовместн.--события, появл-е кот. исключ. др.др. Множ-во элемент. событий отн-но произведен. испытания—простр-во элемент. событий и обознач-ся 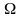(омега).

Случ.событие—люб. множ-во элемент. событий.

Теория вер-ти польз-ся языком теории множеств. События—множ-ва, а действия над событиями– действия над множ-вами. Случ. соб-я обознач-ся больш. латинск. буквами, а числа—маленьк. латинск. буквами. Множ-ва событий—греческ. буквами.

Действия над событиями.

_{1.Если при появлении С. А происх. и С.} B, то говор., что С. А влечет за собой С. В и обознач. А В/ 2.Если А B и В А, то говор., что С. А и В равновозможны и обознач. А=В./ 3.С., состоящее в том, что появится хотя бы одно из С. А или В назыв. суммой С. и обознач-ся А+В./ 4.С., сост. в том, что С. А и В появятся одноврем., назыв. произвед-ем С. и обознач-ся А∙В./ 5.С., сост. в том, что А произойдет, а В не произойдет, назыв. разностью: А-В./ 6.С., сост. в том, что А не произойдет, назыв. противоположн. и обознач-ся ./ 7.С. А и назыв. противоположн., если их одновремен. появл-е невозм-но и в сумме они дают простр-во элемент. С-тий Ø, ./ 8.С. назыв. достоверн., если оно с необход-тью (точно) происх., и обознач-ся Ω (омега)./ 9.С. назыв. невозможн., если оно не м. произойти, и обознач. Ø./ 10.С-я А и В назыв. несовместн., если их одновремен. появл-е невозм-но Ø./ 11.С-я В₁, ..., В_n образуют полн. группу, если люб. 2 из них одноврем. появится не м. и в сумме они дают простр-во элемент. С-тий: Ø,

2. Классич. вер-ть—отнош-е числа исходов m, благоприятствующих наступлению С-я А, к общему чисту n элементарных исходов испытания: Р(А)=m/n. Еще исп-ся обозначение вер-ти—р=Р(А). Формула КВ позвол. решать ограничен. число задач: 1)число элемент. С-тий конечно; 2)все элемент. С-я равновозможны. Теория вер-ти польз-ся языком теории множеств, т.е. С-я это множ-ва, а действия над С-ями–действия над множ-вами. Случ. С-я обознач-ся больш. латинск. буквами, а числа маленьк. латинск. буквами. Множ-ва С-тий—греч. буквами. Св-ва КВ: 1)вер-ть люб. С-я заключена м/у 0 и 1: 0≤Р(А)≤1. 2)вер-ть невозможн. С-я=0: Р(Ø)=0. 3)вер-ть достоверн. С-я=1: Р( )=1. 4)вер-ть суммы несовместн. С-тий=сумме вер-тей этих С-тий, т.е. если А*В=Ø: Р(А+В)=Р(А)+Р(В). 5)вер-ть противоположн. С-я равна: Р(А)=1-Р(А). 6)Если С-е А влечет за собой С-е В, то Р(А)≤Р(В). 7)Теорема сложения: Если С-е А м. представить в виде 2 несовместн. С-я В и С, то вер-ть С-я А равна сумме вер-тей В и С: Р(А)=Р(В)+В(С)

3. Формулы комбинаторики. Гипергеом. Распред-е.

При решении задач с исп-ем формулы Кл. вер-ти часто применяют формулы комбинаторики. Перестановки—

комбинации, составлен. из одних и тех же элементов, кот. отлич-ся только порядком их расположения. Число перестановок из n элементов вычисл-ся по формуле: Р_n=n! Размещения—комбинации, составлен. из n элементов по m (0≤m≤n), кот. различ-ся либо составом элементов, либо порядком их следования. Число размещений из n элементов по m вычисл-ся по формуле:

Сочетания—комбинации, составлен. из n элементов по m (0≤m≤n), кот. различ-ся только составом элементов. Число сочетаний из n элементов по m вычисл-ся по формуле:

Св-ва сочетаний: 1) т.к. по определению 0!=1. 2) 3)

Урновая схема. Пусть в урне имеется N шаров, среди кот. М белых, а ост. черные. Наудачу вытащили k шаров, найти вер-ть того, что среди них l белых.

Эта формула наз. гипергеом. распред-ем