4. Несимметричный режим работы трехфазной цепи

Несимметрия в трехфазной цепи может быть вызвана различными причинами; 1) неодинаковым сопротивлени­ем фаз (несимметричная нагрузка); 2) несимметричным коротким замыканием (например, между двумя фазами или фазой и нейтралью); 3) размыканием фазы; 4) не­равенством величин э. д. с. и т. п.

Расчет токов и напряжений в трехфазной цепи при несимметричном режиме может производиться теми же методами, которые применяются для расчета однофаз­ных цепей.

Рассмотрим несколько простейших вариантов (без взаимной индукции между фазами).

1. Несимметричная трехфазная цепь, соединенная звездой, с нейтральным проводом (рис. 12).

Несимметричная трехфазная цепь, показанная на рис. 12, может рассматриваться как трехконтурная цепь с тремя э. д. с. Такая цепь может быть рассчитана методами контурных токов, узловых напряжений и дру-

гимн. Поскольку в схеме имеются только два узла, наи­более целесообразно в данном случае определить узло­вое напряжение (напряжение смещения) между ней­тральными точками О' и О по формуле, аналогичной (4-4):

(1)

где Y a, Y_B, Yс и Y_N — про­водимости соответствующих ветвей.

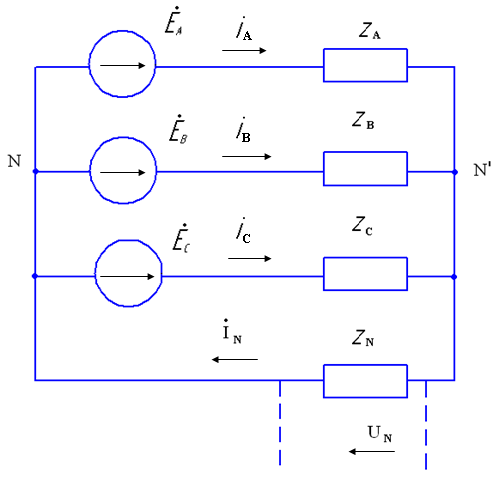
Рис. 12. Несимметричная трехфазная цепь, соединен­ная звездой (с нейтральным проводом).

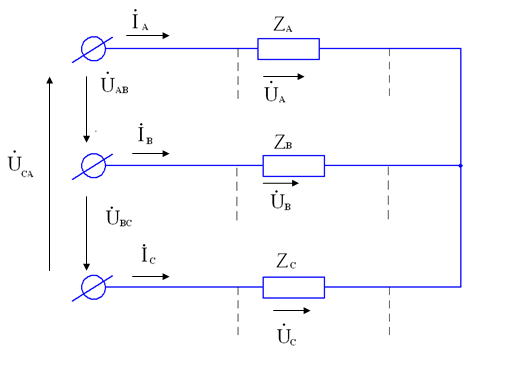
Рис. 13. Несимметричная трехфазная нагрузка, соеди­ненная звездой

(без нейтраль­ного провода).

После этого найдем токи:

İ_A=Y_a( - ₎;

İ_B=Y_B( - ₎;

İ_C=Y_C( - ₎.

В симметричной трехфазной цепи Y_A = Y_B = Y_C и

поэтому при E_A+E_B+E_C = 0 узловое напряжение U_N равно нулю.

Случаю размыкания какой-либо фазы или нейтраль­ного провода соответствует равенство нулю проводимо­сти данной фазы или нейтрального провода.

При отсутствии нейтрального провода, полагая в (1) Y_N= 0, имеем:

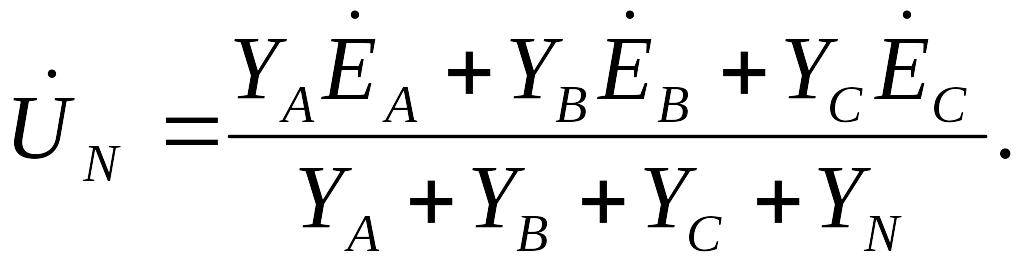
2. Несимметричная трехфазная нагрузка, соединен­ная звездой (без нейтрального провода), с заданными линейными напряжениями на зажимах (рис. 13).

Если заданы линейные напряжения U_AB, 0_BC и оса на зажимах нагрузки, соединенной звездой, то токи в фа­зах звезды определяются следующим образом.

Обозначив фазные напряжения на зажимах нагрузки через U_A, U_B и U_C

(рис. 13), получим

_;

_;

_,

где Y_A, Y_B и Y_C— проводимости фаз нагрузки.

Равенство нулю суммы токов трех фаз записывается в виде:

. (2)

Фазные напряжения U_в и U_c могут быть выражены через U_A и заданные линейные напряжения:

; (3)

_.

Подстановка (3) в (2) дает:

.

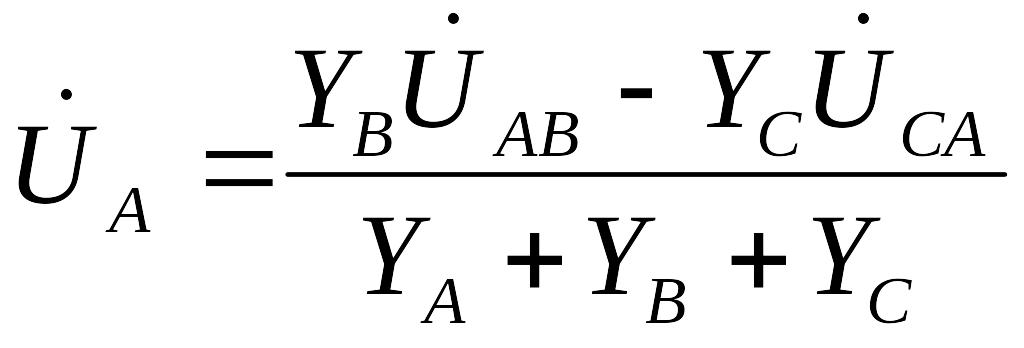Круговой заменой индексов (с порядком следования АВСА и т. д.) находятся:

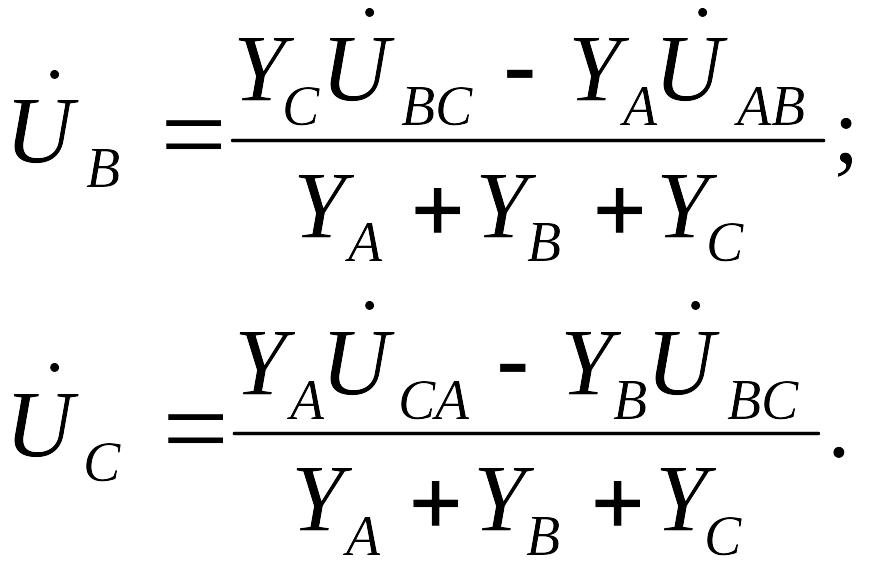(4)

По фазным напряжениям нагрузки находятся фазные токи.

В случае симметричной нагрузки Y_A = Y_B = Y_C век­тор фазного напряжения равен одной трети диагонали параллелограмма, построенного на соответствующих ли­нейных напряжениях. Фазные напряжения в этом случае определяются векторами, соединяющими центр тяжести треугольника напряжений (точка пересечения медиан) с вершинами треугольника,, -

На рис. 14 построение сделано для фазы А по фор­муле (4):

.

В качестве примера рассмотрим схему фазоуказателя, используемую для определения чередования фаз по времени, состоящую из конденсатора и двух одинаковых электрических ламп, соединенных звездой¹.

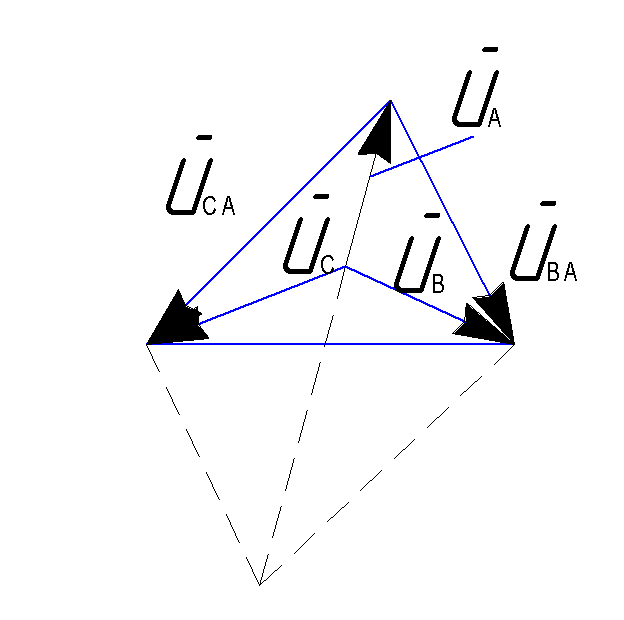
Рис. 14. Нахож­дение фазных на­пряжений.

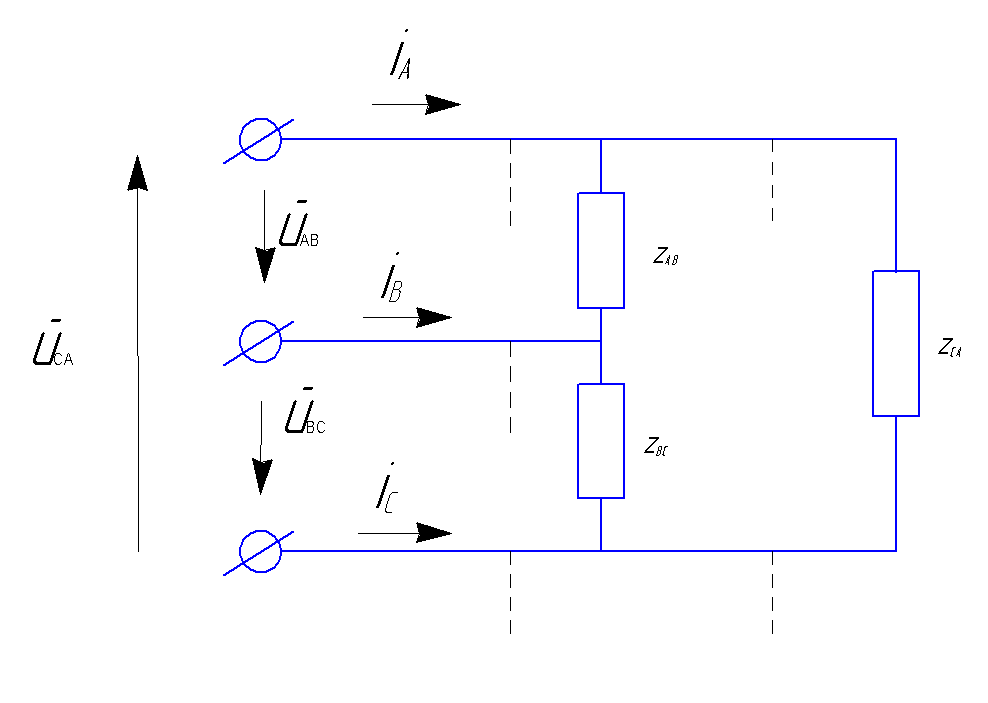
Рис. 15. Несимметричная трехфазная нагрузка, соеди­ненная треугольником.

Положим, что конденсатор присоединен к фазе Л, лампы — к фазам В и С; емкостное сопротивление кон­денсатора берется равным по величине сопротивлению лампы, т. е. Z_A = —jx_c, Z_B = Z_c = r, причем х_с = r.

Неравенство напряжений на лампах проявится в том, что накал ламп будет разным. Отношение напряжений согласно выведенным выше выражениям (4) равно при симметрии линейных напряжений:

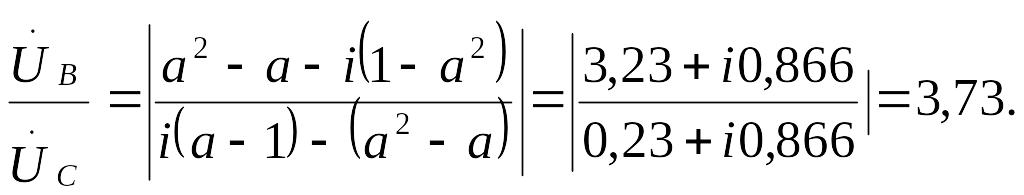
Следовательно, лампа, присоединенная к фазе В (т. е. к фазе, опережающей ту, к которой присоединена вторая лампа), будет светить ярко, а лампа, присоеди­ненная к отстающей фазе, — тускло.

Для определения чередования фаз на практике обычно поль­зуются специальным прибором, в котором создается вращающееся магнитное поле (см. § 12-6), увлекающее за собой диск в ту или дру­гую сторону.

Вместо конденсатора можно применить индуктивную катушку, подобрав ее индуктивное сопротивление приб­лизительно равным по величине сопротивлению лампы. В этом случае ярче будет светить лампа, присоединенная к отстающей фазе. Эти соотношения также могут быть получены непосредственно из векторной диаграммы.

3. Несимметричная трехфазная нагрузка, соединен­ная треугольником, с заданными напряжениями на за­жимах (рис. 15).

Если на зажимах несимметричной трехфазной нагруз­ки, соединенной треугольником, заданы линейные напря­жения uab, ubc и uca (рис. 15), то токи в сопротив­лениях нагрузки равны:

, и .

Токи в линии определяются как разности соответствующих токов нагрузки, например: и т.д.

Если на зажимах несимметричной трехфазной нагруз­ки, соединенной треугольником, заданы фазные напря­жения , и источника, соединенного в звезду, то линейные напряжения на зажимах нагрузки находятся как разности соответствующих фазных напряжений, в результате чего задача сводится к только что рассмот­ренному случаю (рис. 15).

Трехфазная система применяется в России и во всех странах с конца XIX века. По сравнению с однофазной системой имеет следующие преимущества:

1. Обеспечивает экономию проводов при передаче электроэнергии на расстоянии.

2. Трехфазные электрические машины-двигатели и генераторы имеют более высокий к.п.д., чем однофазные.