3. Симметричный режим работы трехфазной цепи

Расчет трехфазной цепи, так же как и расчет всякой сложной цепи, ведется обычно в комплексной форме. Ввиду того что фазные э. д. с. генератора сдвинуты друг относительно друга на 120°, для краткости математиче­ской записи применяется фазовый оператор — комплекс­ная величина

Умножение вектора на оператор а означает поворот вектора на 120° в положительном направлении (против хода часовой стрелки).

Соответственно умножение вектора на множитель а² означает поворот вектора на 240° в положительном нап­равлении или, что то же, поворот его на 120° в отрица­тельном направлении.

Очевидно,

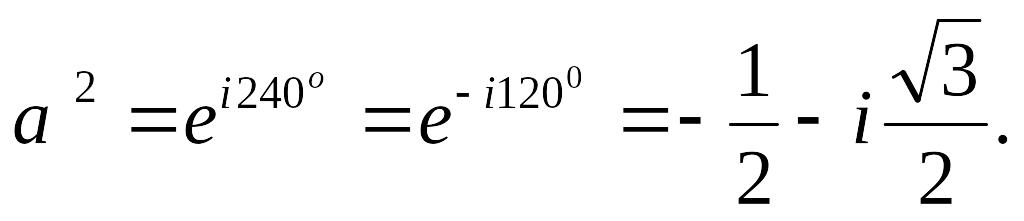
Если э. д. с. фазы А равна _А, то э. д. с. фаз В и С равны соответственно:

В простейшем случае симметричного режима работы трехфазной цепи, когда генератор и нагрузка соединены звездой (рис. 8, а), векторная диаграмма э.д.с. и токов имеет вид, показанный на рис. 8, б.

Ток в каждой фазе отстает от э. д. с. той же фазы на угол = arctg х/r,

где r и х—активное и реактивное сопротивления фаз.

Ток в фазе А находят так же, как в однофазной цепи, потому что нейтральные точки генератора и нагрузки

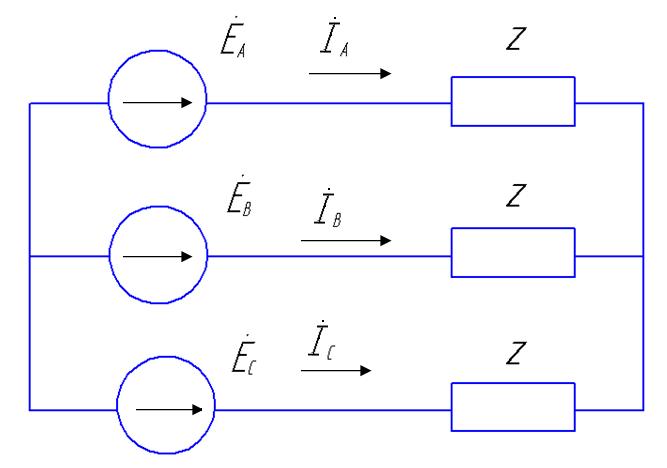
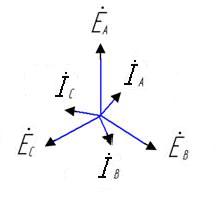
а) б)

Рис. 8. Симметричный режим работы трехфазной цепи.

а — трехфазная цепь; б — векторная диаграмма

в симметричном режиме могут быть соединены как име­ющие одинаковые потенциалы:

·

Соответственно токи в фазах В и С выражаются че­рез ток I_А:

, .

Наличие нейтрального провода не вносит при сим­метричном режиме никаких изменений, так как сумма токов трех фаз равна нулю и ток в нем отсутствует:

.

Таким образом, при симметричном режиме работы трехфазной цепи задача сводится к расчету одной из фаз аналогично расчету однофазной цепи. При этом сопро­тивление обратного (нейтрального) провода не учиты­вается, так как ток в нем и соответственно падение на­пряжения на нем отсутствуют.

По мере удаления от генератора фазные напряжения, определяемые падениями напряжения до нейтральной точки нагрузки, изменяются по величине (обычно убыва­ют) и по фазе. Линейные напряжения определяются как разности соответствующих фазных напряжений, напри­мер: . В любом месте трехфазной линии при симметричном режиме соблюдается следующее соот­ношение между модулями линейных и фазных напря­жений:

Действительно,

т. е. опережает по фазе на 30°, причем модуль Uав в 1/ 3 раз превышает U_A.

В случае соединения треугольником линейные токи определяются в соответствии с первым законом Кирхго­фа как разности фазных токов и при симметричном ре­жиме соблюдается соотношение

Соединение фаз генератора или нагрузки треугольни­ком должно быть для расчета заменено эквивалентным соединением фаз звездой; вследствие этого расчет трех­фазной цепи с соединением фаз треугольником приво­дится в конечном итоге к расчету эквивалентной трех­фазной цепи с соединением фаз звездой.

Между сопротивлениями сторон треугольника (Z_) и лучей звезды (Z_ ) имеет место соотношение Z_ = 1/3 Z_ , вытекающее из формул преобразования треугольника сопротивлений в эквивалентную звезду. Это соотношение справедливо как для сопротивлений сим­метричной трехфазной нагрузки, так и для сопротивле­ний симметричного трехфазного генератора. При этом фазные э. д. с. эквивалентного генератора, соединенного звездой, берутся в раз меньшими фазных э. д. с. за­данного генератора, соединенного треугольником (кроме того, они должны быть сдвинуты на угол 30°). Это легко усмотреть из векторной потенциальной диаграммы нап­ряжений генератора.

Активная мощность симметричной трехфазной на­грузки равна:

.

_Ввиду того, что при соединении нагрузки звездой и , а при соединении нагрузи тре­угольником U_ф = U_л и , активная мощность трехфазной цепи независимо от вида соединения выра­жается через линейные напряжения и ток следующим образом:

здесь ф — угол сдвига фазного тока относительно одно­именного фазного напряжения.

Рис. 9. Измерение активной мощности при симметрич­ном режиме.

Аналогичным образом для реактивной и полной мощ­ностей симметричной трехфазной нагрузки имеем:

; .

Приведенные выражения не означают, что при пере­соединении нагрузки со звезды на треугольник (или на­оборот) активная и реактивная мощности не изменяют­ся. При пересоединении нагрузки со звезды на треуголь­ник при заданном линейном напряжении фазные токи возрастут в раз, а линейный ток — в 3 раза и поэто­му мощность возрастет в 3 раза.

Если нейтральная точка симметричной трехфазной нагрузки выведена, то измерение активной мощности мо­жет быть осуществлено одним ваттметром, включенным по схеме рис. 9, а (одноименные или так называемые генераторные зажимы последовательной и параллельной цепей ваттметра отмечены на рис. 9, а звездочками). Утроенное показание ваттметра равно суммарной актив­ной мощности трех фаз.

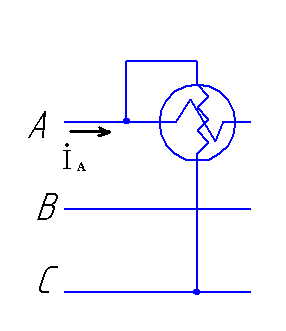
Рис. 10. Изме­рение реактивной мощности при сим­метричном режи­ме.

Если нейтральная точка не выведена или нагрузка соединена треугольником, то можно воспользоваться схемой рис. 9,б , где параллельная цепь ваттметра и два добавочных активных сопротивления r_доб, равные по величине сопротивлению параллельной цепи ваттметра, образуют искусствен­ную нейтральную точку 0 *.

Для получения суммарной мощно­сти, как и в предыдущем случае, по­казание ваттметра утраивается.

На рис. 10 показан способ изме­рения реактивной мощности в симмет­ричной трехфазной цепи при помощи одного ваттметра: последовательная цепь ваттметра включена в фазу А, а параллельная — между фазами В и С, причем генераторные зажимы ваттмет­ра присоединены к фазам А и В. Показание ваттметра в этом случае равно:

U_BC∙I_A∙cos(φ-90⁰)=U_BC∙I_A∙sinφ.

Для получения суммарной реактивной мощности по­казание умножается на .

а) б)

Рис. 11. Пример 11-1.

* Следует заметить, что здесь применим только электродинами­ческий или ферродинамический ваттметр, сопротивление параллель­ной цепи которого является чисто активным. Индукционный ватт­метр неприменим по той причине, что сопротивление параллельной цепи такого ваттметра имеет реактивное сопротивление; для созда­ния искусственной нейтральной точки в этом случае потребовались бы реактивные добавочные сопротивления.

Разделив активную мощность на полную мощность, получим:

Cos φ= P/S

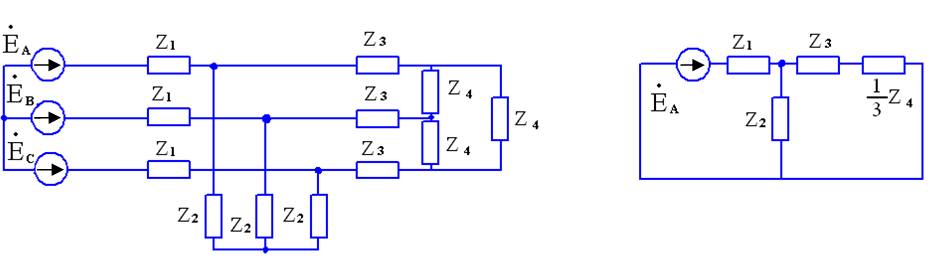
Пример 11-1. Определить ток в генераторе при симметричном режиме работы трехфазной цепи, представленной на рис. 11, а.

Сопротивления Z₄, соединенные треугольником, заменяются экви­валентной звездой из сопротивлений — 1/3 Z_4.

При симметричном режиме нейтральные точки генератора и на­грузки, как было указано выше, могут быть объединены. Тогда ре­жим работы каждой фазы, например фазы А, может быть рассмот­рен в однофазной расчетной схеме (рис11, б).

Результирующее сопротивление цепи одной фазы равно:

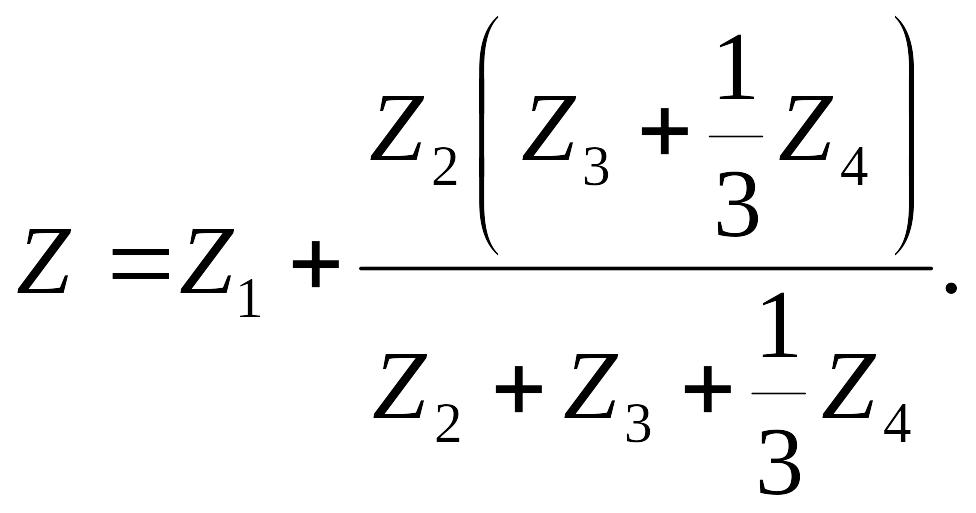
Искомый ток в фазе А