17.Інтервальні шкали. Періодичні шкали. Шкали відношень. Абсолютні шкали.
Інтервальна шкала – є наступною за силою після порядкової. Відноситься до кількісних шкал. Для любих двох вимірів можна вказати інтервал між ними. В шкалі є упорядкованість, інервальність, але немає нульової точки. Приклад: висота місцевості, температура. Час: від народження Христа, вимір відносно Чорного моря.. До інтервальної шкали відносяться шкала різниць(циклічна). Наприклад циферблат год. Шкала відношень. Над числами вимірювання можна виконувати арифметичні дії – це пояснюється тим, що тут присутні всі атрибути вимірювань шкал і нульова точка. Пр.вага, довжина.
Абсолютна шкала. Кожна абс. Шкала має абс.0 і абс.1. Це дозволяє вимірювати деяку властивість в деяких одиницях. Пр. кг, см, В.Для вимірювань використовуються шкала дійсних чисел: від’ємні,раціональні, ірраціон. Характерним приклад шкали є числова вісь. Показник який вимір в абс. шкалі може бути використаний у любих мате мат.операціях
18. Типи невизначеності даних. Випадковість.
При проведенні вимірювань стикаються з поняттям невизначеності. Розрізняють 2 види: випадковість і нечіткість. Випадковість - це невизначеність, яка описується деяким законом розподілу. Знаючи такий закон можна визначити інтервальні зміни ВВ, її середнє значення та розсіювання. Якщо ми знаємо сер. Значення ВВ і її розсіювання – цього достатньо для вирішення будь-якої практичної задачі.
19 Нечіткість даних. Лінгвістичні змінні. Функція належності.
Нечіткість – другий вид невизначеності. Є багато характеристик, які не можливо точно оцінити числом. Їх оцінюють деякими мовними виразами, інструкціями. Напр: висока людина, холодний день. Лінгвістична змінна – це словесна конструкція, яка виражає деяку якість об’єкта. Лінгвістичні змінні використовують в теорії не чітких множин. Нечітка множина складається з групи об’єктів, для того, щоб виявити чи не належить об’єкт до чіткої множини використовують функцію належності. Основою характеристикою нечіткої змінної є функція яка має такі властивості:
Розглянемо оцінку успішності студента.
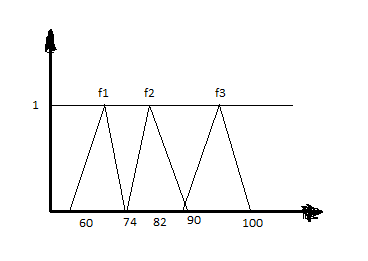
0≤ f(x) ≤1.Якщо F(x)=0 – елемент не належить площині
F(x)=1- точка належить площині.
Інколи не чіткі множини задають за допомогою впорядкованих пар.
20. Класифікаційні моделі даних. Класифікація, кластеризація, упорядкування, зменшення розмірності.
Для аналізу даних використовують різні моделі даних. Їх поділяють на 2 групи: класифікаційні та числові. В свою чергу класифікаційні поділ:
Кластеризація – групування об’єктів за деякою ознакою
Класифікація – розпізнавання.
Задається кількість класів. Кожен об’єкт треба віднести до одного з класів. Напр: студентська група.
Упорядкування – пр. рейтинг успішності.
Зауваження: при класифікації об’єктів часто стикаються з проблемою розмірності. Об’єкт має ряд ознак, при тому деякі з них можуть бути зайвими і заважати класифікації. Числові моделі відрізняються від класифікаційних тим, що всі ознаки визначені числом. Між цими ознаками існують зв’язки.
Розглянемо приклади числових моделей:
Непрямі вимірювання(чорний ящик, прогнозування)
Пошук екстремуму. Більшість економічних задач вимірюються знаходженням найбільшої величини прибутку або найменшої величини витрат. Для розв’язання таких задач спеціально створена теорія оптимізації.