Канал с помехами

Если в канале есть помехи, то в этом случае мы должны учесть вероятности получения символов, потери

Скорость передачи информации всегда определяется относительно первичного алфавита и зависит от его энтропии.

Скорость передачи сигналов определяется по формуле

Так как скорость передачи информации зависит от информационных характеристик источника сообщений (Н), а скорость передачи сигналов от быстродействия аппаратуры, поэтому они вычисляются по разным формулам.

Рассмотрим случаи:

1) равновероятностные и взаимонезависимые символы:

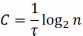
2) неравновероятные символы равной длины:

Пропускная способность (емкость канала связи) – это максимальная скорость передачи информации по данному каналу связи.

При наличии помех пропускная способность канала связи вычисляется как произведение количества принятых в секунду знаков на разность энтропии источников сообщений и условий энтропии источников сообщений относительно принятого сигнала.

Если символы источников сообщений не равновероятны и взаимозависимы, то энтропия источника считается по формуле общей условной энтропии.

Действие помех в канале связи так же может быть подсчитано по формуле условной энтропии.

Противоречий здесь нет, так как в этом случае в формулах условной энтропии будут использованы разные условные вероятности.

В первом случае это будут условные вероятности появления одного символа в зависимости от появления вероятностей некоторого другого символа, а во втором случае – условные вероятности перехода одного символа к другому под действием помех в канале связи.

Безусловные вероятности появления символов на выходе источника сообщений или на входе приемника должны быть известны заранее или определены по условию.

Скорость передачи информации зависит от экономичности вторичного алфавита. Чем больше избыточность кода, тем ниже скорость передачи.

Абсолютная избыточность = H_max-H

Относительная избыточность = 1-H/H_max

Избыточность показывает, какая доля максимально возможной неопределенности (энтропии) не использована источником.

Следствием ограничений на выбор источником знаков является недоиспользование их как переносчиков информации. Все алфавиты неравных языков обладают избыточностью и достигается она в среднем на 50%.

Грубо говоря, 50% и более передаваемых символов являются лишними и могли бы не передаваться, если бы не опасность искажения.

Кодирование данных

Кодирование – это преобразование дискретного сообщения из одного алфавита в другой, причем, как правило, от алфавита с большей мощностью к алфавиту с меньшей (10  2).

Сам процесс кодирования представляет собой процесс преобразования первичного сообщения в последовательность кодовых символов.

Пример дискретного сообщения – текст.

Вся совокупность (цифр, букв, знаков препинания) называется алфавитом источника, а так как их алфавит конечен, то все символы можно пронумеровать и свести передачу сообщения к передаче последовательных чисел.

В реальных системах кодирование осуществляется в двоичной системе.

Кодовая комбинация – количество разрядов (позиций), которая занимает последовательность символов и берется из вторичного алфавита

Q=n^l

n – алфавит {0,1} = 2

l – длина

l = log₂10

M = (Арус. яз.) = 32

l = log₂32 = 5 бит/буква

l = 2 log₂MA