2.4. Непрерывный источник. Взаимная информация для непрерывных ансамблей. Относительная (дифференциальная) энтропия.

Рассматривавшиеся до сих пор дискретные ансамбли сообщений не исчерпывают всего многообразия вариантов, встречающихся на практике. Значительный интерес представляют и непрерывные ансамбли, которым посвящен настоящий параграф.

Как уже упоминалось, в качестве модели непрерывного ансамбля в теории информации используется континуальное множество , на котором задана соответствующая плотность вероятности . Тем самым рассматриваемый тип непрерывных ансамблей отождествляется с числовой осью. Распространение понятия взаимной информации на непрерывные ансамбли не встречает затруднений и состоит в обычном предельном переходе.

Пусть имеются два непрерывных ансамбля с заданной двумерной плотностью вероятности . Понятно, что одномерные плотности можно получить из интегрированием по «ненужной» переменной

и далее, если потребуется, найти условные плотности вероятности и из правила умножения вероятностей

.

Для того чтобы воспользоваться ранее полученными результатами, удобно ввести в рассмотрение дискретные ансамбли и , полученные равномерной дискретизацией по уровню (квантованием) непрерывных ансамблей и с шагом квантования . Иллюстрацией этому служит рис. 2.3.

Квантование по уровню заключается в замене значения непрерывной случайной величины дискретным значением , удовлетворяющим условию . Поэтому вероятность принятия величиной значения находится как

,

где последнее приближение справедливо при достаточно малом .

Рис. 2.3

Аналогично , и , где . Тогда согласно (2.11) средняя взаимная информация дискретных ансамблей и

.

При ансамбли и приближаются к непрерывным и , а операция суммирования заменяется интегрированием, что приводит к определению средней взаимной информации непрерывных ансамблей в следующем виде:

. (2.22)

Замечание. Практически все свойства средней взаимной информации являются общими для дискретных и непрерывных ансамблей. Единственное отличие состоит в том, что для непрерывных ансамблей не определена собственная информация и, следовательно, оказывается невозможным представление ее разностью энтропий. Однако можно ввести некоторые аналоги энтропий и в непрерывном случае, получив выражение, подобное (2.14). Для этого запишем выражение для энтропии ансамбля в виде

. (2.23)

С учетом того, что при , соотношение (2.23) принимает вид

,

где – "предел" второго слагаемого в (2.23).

Таким образом, энтропия ансамбля при стремится к бесконечности, что согласуется с представлением об энтропии как о мере неопределенности, поскольку при неограниченном возрастании числа элементов ансамбля его неопределенность также увеличивается беспредельно.

Однако, если в соответствии с (2.14) рассматривать взаимную информацию, как разность безусловной и условной энтропий, то слагаемые , не зависящие от конкретного ансамбля, компенсируются и не влияют на результат. В связи с этим для характеристики непрерывных источников используют понятие относительной или дифференциальной энтропии.

Относительной (дифференциальной) энтропией непрерывного источника называется величина

. (2.24)

Аналогично соотношению (2.24) можно записать выражение и для условной относительной энтропии

, (2.25)

так что в согласии с (2.14) и (2.22)

. (2.26)

Несмотря на большую степень общности между относительной энтропией и энтропией дискретного источника у первой имеется некоторая специфика. Так, относительная энтропия может принимать не только положительные, но и отрицательные значения.

Пример 2.4.1. Пусть плотность вероятности для некоторого непрерывного ансамбля равномерна на отрезке , т. е.

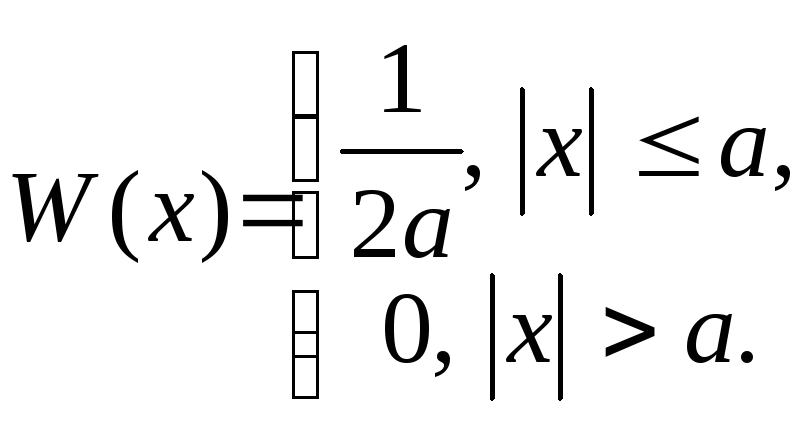(2.27)

Тогда относительная энтропия этого ансамбля

.

Как видно, при значение , тогда как случай отвечает .

Пример 2.4.2. Пусть плотность вероятности для непрерывного ансамбля распределена по нормальному (гауссовскому) закону с нулевым средним и дисперсией , т.е.

. (2.28)

Тогда

, (2.29)

поскольку . Очевидно, что, как и в примере 2.4.1, относительная энтропия может быть как положительной, так и отрицательной в зависимости от значения дисперсии.