Тема 4. Пропускная способность каналов связи.

4.1. Пропускная способность (информационная емкость) дискретного канала без памяти.

Пусть, как и ранее, на вход дискретного канала без памяти (ДКБП) поступает последовательность символов , гдепринадлежат некоторому множеству (алфавиту)X, а . На выходе канала наблюдается последовательность , принадлежащая множеству. В соответствии с определением ДКБП переходные вероятности задаются соотношением

,

где в стационарном случае  вероятность превращения входного символа в выходной(переходная вероятность на символ) не зависит от дискретного времени, т.е., гдеи. Покажем, что при этом пропускная способность канала определяется только алфавитами входных и выходных символов и переходной вероятностьюна символ.

Ансамбли входных и выходныхпоследовательностей можно рассматривать как произведения ансамблейисоответственно, гдеи,– ансамбли входных и выходных символов вi-й момент времени, причем, как указывалось ранее, идля любыхi. Тогда согласно правилу аддитивности энтропии (2.20)

и свойству не убывания энтропии по мере роста объема наблюдений (2.17)

,

справедлива оценка

. (4.1)

С другой стороны, при заданных входных символах выходные символыДКБП независимы и в силу аддитивности энтропии

.

Таким образом, , откуда в соответствии с (2.30) следует, что верхняя граница средней взаимной информации на символ (или информационная емкость) ДКБП, определяется как

, (4.2)

где учтено, что определяется лишь статистикойотдельного символа.

Убедимся, что равенство в (4.2) достигается тогда, когда ансамбли статистически независимы. Для ДКБП данное условие выполняется, если входные символы статистически независимы, т.е. если. Действительно, по теореме умножения вероятностей

,

так что

.

Как и утверждалось, независимость символов входной последовательности гарантирует независимость символов выходной, а значит, совпадение всех условных энтропий с безусловнойи равенство в соотношении (4.1). Тем самым обеспечивается и равенство, максимизация правой части которого по распределениюдаст правую часть (4.2). Это означает, что средняя взаимная информация на символ(точнее, ее верхняя грань) в реальности максимизируется до предела, указываемого (4.2), и, тем самым, информационная емкость ДКБП

. (4.3)

Поскольку , из полученного результата следует, что информационная емкость ДКБП при заданных входном и выходном алфавитах зависит только от символьной переходной вероятности: энтропияопределяется лишь распределением, по которому осуществляется максимизация, азависит помимо распределениятолько от.

4.2. Информационная емкость двоичного симметричного канала без памяти.

Проиллюстрируем сказанное на примере ДСК без памяти (ДСКБП), задаваемого моделью, представленной на рис. 1.4, и описываемого переходными вероятностями

,.

Пусть – вероятность появления на входе канала. Тогда согласно (2.13)

,

поскольку при любом на выходе канала возможны только два состояния с вероятностямиp и , и значит,

.

Таким образом, условная энтропия не зависит от распределения вероятностей на входе, поэтому максимизациясводится к максимизации только¹.

В соответствии с (2.4) максимум , равный 1, достигается при равной вероятности выходных символов. Поскольку

, ,

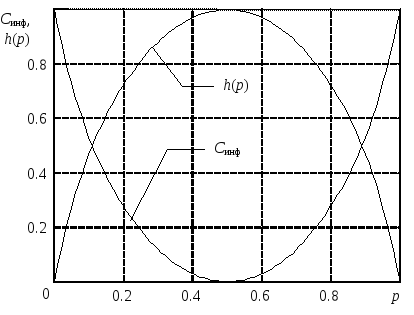
то данное требование автоматически удовлетворяется при равновероятности входных символов, т.е. . В итоге информационная емкость ДСКБП

. (4.4)

Рис. 4.1

Графики ив зависимости отp представлены на рис. 4.1, из которого следует, что информационная емкость уменьшается от 1 до 0 с ростом p от 0 до 0,5. Точка , отвечает так называемому обрыву канала: наименование отражает факт невозможности сколько-нибудь достоверной передачи в условиях, когда любой переданный символ с равной вероятностью может либо сохранить свое значение, либо трансформироваться в противоположный. Симметрия кривой относительно точкиозначает, что каналы, имеющие вероятности ошибки на символp и 1p , полностью эквивалентны. В самом деле, если вероятность ошибки , то можно просто переобозначить выходные символы, считая нуль единицей и наоборот. Тем самым вероятность ошибки на символ будет сделана равной 1p , т. е. меньше 0,5.