
- •1.Вклад русских и зарубежных ученых в развитие электротехники
- •2 Соединение трехфазных потребителей в «звезду»
- •3.Основные сведения об электрическом поле
- •4.Первый закон Киргофа
- •5.Энергия электрического поля. Энергия магнитного поля.
- •6.Линейная цепь переменного тока с реальным конденсатором
- •7.Соединение трехфазных потребителей в «треугольник»
- •8.Напряженность электрического поля
- •10.Поляризация диэлектриков. Виды поляризации.
- •11.Магнитные цепи. Прямая и обратная задачи
- •12.Последовательное соединение индуктивности и емкости на переменном токе.
- •17.Разветвленная неоднородная магнитная цепь
- •18.Напряжение в электрическом поле
- •19.Закон электромагнитной индукции
- •20.Пробой диэлектриков. Виды пробоев
- •21.Заряд-разряд конденсатора
- •22.Электрический ток проводимости
- •23.Параллельное соединение пассивных элементов
- •24.Электрическая емкость
- •25.Трехфазное напряжение
- •26.Величина и направление электрического тока
- •27. Смешанное соединение пассивных элементов. Метод свертывания.
- •28.Соединение конденсаторов.
- •29.Правило правой руки
- •30.Закон Ома
- •31.Последовательное соединение индуктивности и емкости на переменном токе
- •32.Теорема Остроградского-Гаусса
- •33.Преобразование «треугольника» сопротивлений в звезду Причина преобразования треугольника в звезду
- •Формулы для расчета преобразования треугольника в звезду
- •34. Закон коммутации
- •35.Взаимное преобразование электрической и механической энергии
- •36.Сверхпроводимость
- •37.Линейная цепь переменного тока с реальным конденсатором
- •38.Магнитный поток, магнитосцепление
- •39.Преобразование «звезды» сопротивлений в треугольник
- •40.Линейная цепь переменного тока с реальной индуктивностью
- •41.Сверхпроводимость
- •42.Метод узловых напряжений
- •43.Магнитное поле цилиндрической катушки
- •44.Метод узловых и контурных уравнений
- •Метод контурных токов
- •45.Фазное и линейное напряжение
- •46.Векторная диаграмма
- •47.Электрическая цепь и ее основные элементы
- •48.Метод контурных токов
- •49.Взаимоиндуктивность
- •50.Линейные цепи переменного тока. Цепь с активным сопротивлением
- •Цепь переменного тока с индуктивным сопротивлением.
- •51.Фазные и линейные токи
- •Четырехпроводная система трехфазного тока
- •52.Закон электромагнитной индукции
- •53.Источники электрической энергии
- •54.Закон Кулона
- •55.Магнитное поле в ферромагнитиках
- •56.Разветвленная неоднородная магнитная цепь
- •57.Закон Ленца
- •58.Реактивная мощность. Поверхностный эффект
- •59.Напряженность магнитного поля
- •60.Магнитные цепи. Прямая и обратная задачи
- •61.Соединение трехфазных потребителей в «звезду»
- •62.Магнитное сопротивление
48.Метод контурных токов
Метод контурных токов – один из основных и широко применяемых на практике методов. Он заключается в определении по второму закону Кирхгофа контурных токов. Для каждого контура цепи задают ток, который остается неизменным. В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно.
Контурные токи, проходя через узел, остаются непрерывными. Следовательно, первый закон Кирхгофа выполняется автоматически. Уравнения с контурными токами записываются только для второго закона Кирхгофа. Число уравнений, составленных по методу контурных токов, меньше чем по методу законов Кирхгофа.
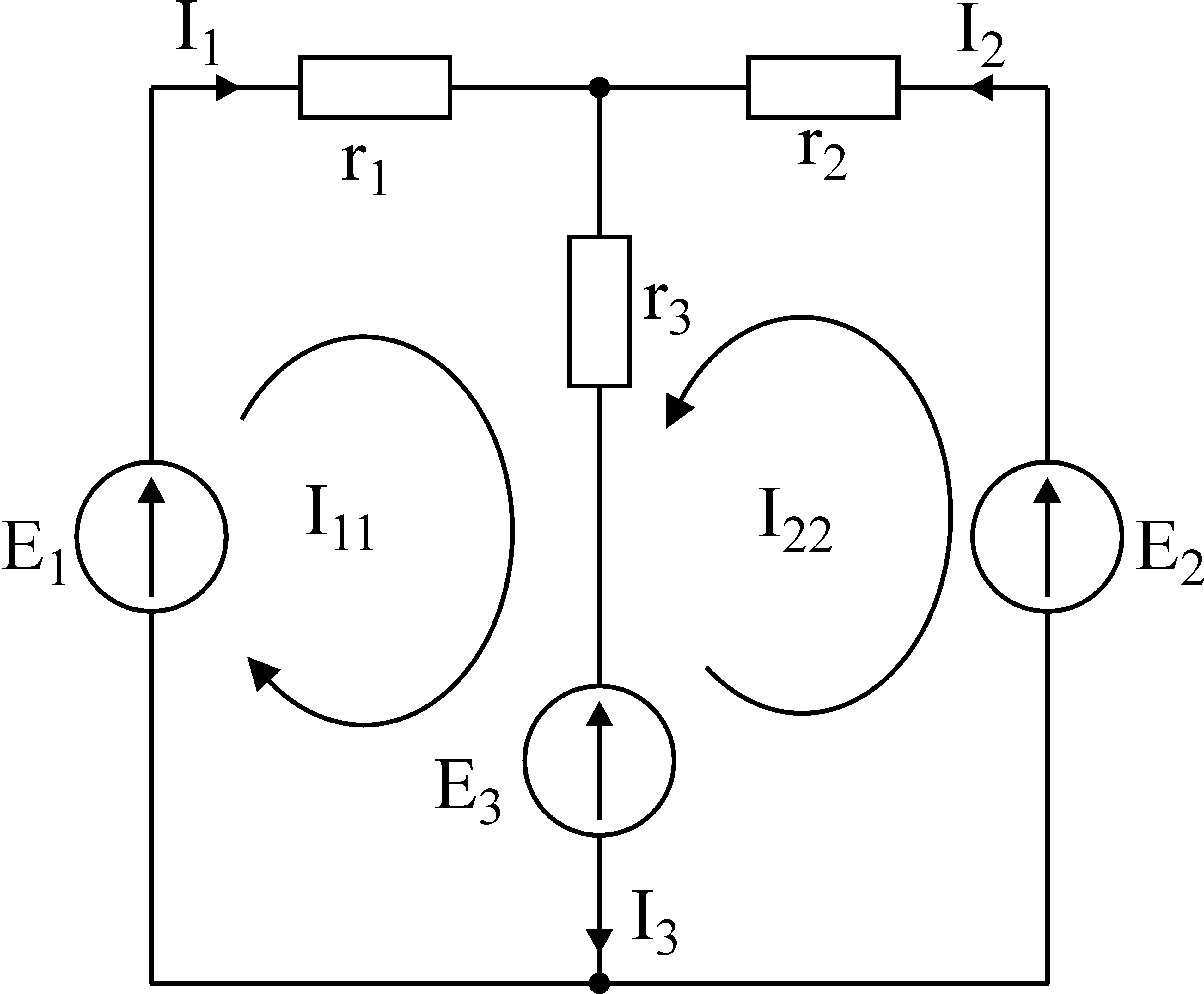
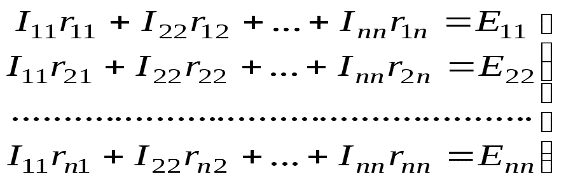
Рис.28. Иллюстрация к методу контурных токов. (29)
На рис.28 показана цепь с двумя независимыми контурами, следовательно, и с двумя контурными токами I11иI22.
Токи в ветвях I1иI2равны контурным токам:
I1=I11, I2=I22
Ток I3равен сумме этих двух контурных токов:
I3=I11+I22
По второму закону Кирхгофа для первого контура цепи:
I1r1+I3r3=E1-E3
Или: I11r1+(I11+I22)r3=E1-E3;
I11 (r1+r2)+I22r3=E1-E3
Обозначим r1+r2=r11
r3=r12; E1-E3
Тогда: I11r11+I2r12=E11
r11– сумма всех сопротивлений, входящих в контурI, называетсясобственным сопротивлением контура.
r12– сопротивление ветви, общей для контураIиII;
E11=E1-E2– алгебраическая сумма всех э.д.с., содержащихся в первом контуре; со знаком «-» берется э.д.с., действующая навстречу контурному току рассматриваемого контура.
E11называетсяконтурной э.д.с.
Аналогично для второго контура рис.28.
I11r21+I22r22=E22,
где r21=r3;r22=r2+r3;
E22=E2-E3
Уравнения, составленные по методу контурных токов, всегда записывают в виде системы. Для схемы рис.28:

В результате решения системы находят контурные токи, а затем токи ветвей.
Если заданная электрическая цепь содержит nнезависимых контуров, то на основании второго закона Кирхгофа получаетсяnконтурных уравнений:
Собственные сопротивления riiвходят в уравнения (29) со знаком «+», поскольку обход контура принимается совпадающим с положительным направлением контурного токаIii. Общие сопротивленияrikвойдут в уравнения со знаком «-», когда токиIiиIkнаправлены в них встречно.
Число уравнений, составляемых по методу контурных токов, определяется по формуле:
Nур=Nb-Ny+1-Nи.т.
где Nb– число ветвей электрической цепи;
Ny– число узлов;
Nи.т.– число идеальных источников тока.
Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.
49.Взаимоиндуктивность
Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одномпроводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимногорасположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитнойиндукции. При изменении тока в одном из проводников или при изменении взаимного расположенияпроводников происходит изменение магнитного потока через (воображаемую) поверхность, "натянутую" наконтур второго, созданного магнитным полем, порожденным током в первом проводнике, что по законуэлектромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводникзамкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего привзаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи(катушке) встречает противодействие со стороны другой цепи (катушки).
Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукциямежду цепями. С количественной стороны явление взаимоиндукции характеризуется взаимнойиндуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величиныиндуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменениявзаимоиндукции между цепями, называются вариометрами связи.
Явление взаимоиндукции широко используется для передачи энергии из одной электрической цепи в другую, для преобразования напряжения с помощью трансформатора.
