
Аксиомы статики и их следствия.
Аксиома 1.
Тело
под действием силы приобретает ускорение
и не может находиться в покое. Первая
аксиома ставит условия, при выполнении
которых система сил будет уравновешена.
Аксиома 1. Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю) тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны. Это означает, что если абсолютно твердое тело находится в покое под действием двух сил, то эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны. Обратно, если на абсолютно твердое тело действуют по одной прямой в противоположные стороны две равные по модулю силы и тело в начальный момент находилось в покое, то состояние покоя тела сохранится.

На рис. 1.4 показаны уравновешенные силы F1, F2 и Р1, Р2, удовлетворяющие соотношениям: (F1,F2)~0, (P1,Р2)~0. При решении некоторых задач статики приходится рассматривать силы, приложенные к концам жестких стержней, весом которых можно пренебречь, причем известно, что стержни находятся в равновесии. Из сформулированной аксиомы действующие на такой стержень силы направлены вдоль прямой, проходящей через концы стержня, противоположны по направлению и равны друг другу по модулю (рис. 1.5, а). То же самое и в случае, когда ось стержня криволинейная (рис. 1.5, б).
Аксиома 2.

Аксиома 2. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему, в частности, если эта система состоит из двух сил, равных по модулю, действующих по одной прямой и направленных в противоположные стороны. Из этой аксиомы вытекает следствие: не нарушая состояния тела, точку приложения силы можно переносить вдоль линии ее действия.Действительно, пусть сила FА приложена к точке А (рис. 1.6, а). Приложим в точке В на линии действия силы FA две уравновешенные силы FB и F'B, полагая, что FB=FA (рис. 1.6, б). Тогда согласно аксиоме 2 будем иметь FA~FA, FB, F`B). Так как силы FА и FB обра зуют также уравновешенную систему сил (аксиома 1), то согласно аксиоме 2 их можно отбросить (рис. 1.6,в). Таким образом, FA~FA,FB,F`B)~FB, или FA~FB, что доказывает следствие. Это следствие показывает, что сила, приложенная к абсолютно твердому телу, представляет собой скользящий вектор. Обе аксиомы и доказанное следствие нельзя применять к деформируемым телам, в частности, перенос точки приложения силы вдоль линии ее действия меняет напряженно-деформированное состояние тела.
Аксиома 3.


Аксиома 3. Не меняя cостояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в той же точке и равной их геометрической сумме (аксиома параллелограмма сил). Эта аксиома устанавливает два обстоятельства: 1) две силы F1 и F2 (рис. 1.7), приложенные к одной точке, имеют равнодействующую, т. е. эквивалентны одной силе (F1,F2)~R; 2) аксиома полностью определяет модуль, точку приложения и направление равнодействующей силы R=F1+F2.(1.5) Другими словами, равнодействующую R можно построить как диагональ параллелограмма со сторонами, совпадающими с F1 и F2. Модуль равнодействующей определится равенством R=(F12+F22+2FlF2cosa)1/2, где а—угол между данными векторами F1 и F2. Третья аксиома применима к любым телам. Вторая и третья аксиомы статики дают возможность переходить от одной системы сил к другой системе, ей эквивалентной. В частности, они позволяют разложить любую силу R на две, три и т. д. составляющие, т. е. перейти к другой системе сил, для которой сила R является равнодействующей. Задавая, например, два направления, которые лежат с R в одной плоскости, можно построить параллелограмм, у которого диагональ изображает силу R. Тогда силы, направленные по сторонам параллелограмма, составят систему, для которой сила R будет равнодействующей (рис. 1.7). Аналогичное построение можно провести и в пространстве. Для этого достаточно из точки приложения силы R провести три прямые, не лежащие в одной плоскости, и построить на них параллелепипед с диагональю, изображающей силу R, и с ребрами, направленными по этим прямым (рис. 1.8).
Аксиома 4.

Аксиома 4 (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны. Заметим, что силы взаимодействия двух тел не составляют систему уравновешенных сил, так как они приложены к разным телам. Если тело I действует на тело II с силой Р, а тело II действует на тело I с силой F (рис. 1.9), то эти силы равны по модулю (F = Р) и направлены по одной прямой в противоположные стороны, т. е. F= –Р. Если обозначить через F силу, с которой Солнце притягивает Землю, то Земля притягивает Солнце с такой же по модулю, но противоположно направленной силой – F. При движении тела по плоскости к нему будет приложена сила трения Т, направленная в сторону, противоположную движению. Это– сила, с которой неподвижная плоскость действует на тело. На основании четвертой аксиомы тело действует на плоскость с такой же силой, но ее направление будет противоположно силе Т.
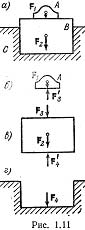
На рис. 1.10 показано тело, движущееся вправо; сила трения Т приложена к движущемуся телу, а сила Т'= –Т — к плоскости. Рассмотрим еще покоящуюся систему, изображенную на рис. 1.11, а. Она состоит из двигателя А, установленного на фундаменте В, который в свою очередь находится на основании С. На двигатель и фундамент действуют силы тяжести F1 и F2 соответственно. Также действуют силы: F3– сила действия тела А на тело В (она равна весу тела А); F`з – сила обратного действия тела В на тело А; F4 – сила действия тел А и В на основание С (она равна суммарному весу тел А и В); F`4– сила обратного действия основания С на тело В. Эти силы показаны на рис. 1.11, б, в, г.Согласно аксиоме 4 F3=–F`3, F4=–F`4, причем эти силы взаимодействия определяются заданными силами F1 и F2. Для нахождения сил взаимодействия необходимо исходить из аксиомы 1. Вследствие покоя тела А (рис. 1.11,6) должно быть F з=–F1, а значит, F3=F1. Точно так же из условия равновесия тела В (рис. 1.11, в) следует F`4=–(F2+F3), т. е. F`4=–(F1+F2) и F4=F1+F2.
