2 Описание и анализ существующих методов

2.1 Анализ творческого обучения в терминах искусственных нейронных сетей

Работа [2] представляет некоторые первые результаты, относящиеся к использованию нейронных сетей, полученные из проекта (Мэммерт, Университет Хайдельберга, Германия, Мэммерт и Перл, 2005) рассматривают детскую обучаемость в играх.

Первый вопрос – могут ли временные ряды, представляющие успешное обучение, быть проанализированы с использованием функциональных карт Кохонена (KFM) для поиска и выборки уникальных классов, независимых от времени шаблонов обучения.

Второй вопрос – могут ли нейронные сети быть использованы для симуляции подобных процессов обучения для планирования конечности и оптимизации этих процессов в отдельности.

Несмотря на незначительные отрытые вопросы, первая проблема может быть решена при помощи динамически управляемой нейронной сети (DyCoN, Перл, 2001), которая является производной от функциональных карт Кохонена и может обучаться неразрывно. Классы шаблонов обучения могут быть вычислены из специфичности каждой конкретной модели обучения.

Для решения второй проблемы концепт динамически управляемой нейронной сети должен быть дополнен некоторыми свойствами естественного обучения.

Первый аспект – динамически подстраивать размер нейронной сети к требованиям процесса обучения – это можно сделать, интегрировав концепт растущего нейронного газа (GNG, Фрицке, 1995).

Второй аспект – позаботиться о редко возникающих событиях с высокой релевантностью, таких же, как творческие процессы, которые пренебрегаются всеми известными топологиями нейронных сетей.

Результатом данной работы стал концепт динамически управляемого нейронного газа (DyCoNG, Бишоф, Герарц, 2006), который сочетает концепты динамически управляемой нейронной сети и растущего нейронного газа, качественными нейронами, которые отражают качество информации. Таким образом, можно измерить творческую составляющую произошедших событий.

Первые результаты симуляций, основанных на динамически управляемом нейронном газе, показывают, что нейронная сеть может повторить записанные процессы обучения и определить основные классы этих процессов.

2.2 Растущий нейронный газ

Растущий нейронный газ (здесь и далее по тесту [3]) представляется как накопительная модель нейронной сети, которая имеет возможность изменять важные топологические связи для данного набора входящих векторов в понятиях простого Хеббовского правила обучения. В отличие от предыдущих предложений, таких как нейронный газ (Мартинец, 1991, Шультен, 1994) эта модель не содержит параметров, которые изменяются во времени, и, соответственно, может обучаться неразрывно, добавляя узлы и связи, до тех пор, пока не будет, достигнут критерий достаточности. Приложения модели включают вектор квантификации, кластеризацию и интерполяцию.

В обучении без учителя доступны только входящие данные и никакой информации о желаемом отклике. Что может быть целью обучения в этом случае?

Одной из возможных целей является понижение размерности – поиск подпространств пространства входящего вектора, которые содержат большую часть или все входящие данные. Линейное подпространство с этим свойством может быть вычислено напрямую из принципиального анализа компонент или итеративно различными моделями нейронных сетей (Санджер, 1989, Ойя, 1982). Функциональная карта Кохонена (Кохенен, 1982) и структуры растущих клеток (Фрицке, 1994) позволяют выполнять проекцию на нелинейные, дискретно разделенные подпространства, которые имеют размерность заданную априори. В зависимости от связи между размерностью производных данных и размерностью целевого пространства, некоторая входящая информация, расположенная в топологии сети может быть потеряна при этом процессе. Это и неудивительно, так как обратное отображение высоко-размерных данных в низко-размерные пространства или структуры не может существовать в принципе.

Вопрос о том, как структуры должны выглядеть для обратного отображения напрямую ведет к другой возможной цели обучения без учителя, которая описывается как обучение топологии – имея некоторое высоко-размерное распределение данных P(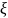 ), найти топологическую структуру, которая наиболее близко отображает топологию распределения данных. Лаконичным методом для построения таких структур является конкурентное Хеббовское обучение (CHL, Мартинец, 1993). Конкурентное Хеббовское обучение требует использования некоторого вектора квантификации. Мартинец и Шультен предложили концепцию нейронного газа (NG) для этой цели (Мартинец и Шультен, 1991).

Кратко рассмотрим и обсудим подход Мартинца и Шультена, и, затем, рассмотрим предложенную новую нейросетевую модель с использованием конкурентного Хеббовского обучения. В отличие от вышеупомянутой связки конкурентного Хеббовского обучения и нейронного газа данная модель является накопительной и имеет только константные параметры. Это приводит к определенным преимуществам по отношению к предыдущему подходу.