Удельная поверхность кернов в м2/м3 некоторых нефтяных месторождений Советского Союза (по ф. И. Котяховуи л. И. Рубинштейну)

№ образца	Ташкала	Ромашкино	Туймазы
1	121500	73000	38000
2	214000	85000	54000
3	330000	113000	52000
4	191000	72500	55000
5	56600	73000	90000

По результатам исследований Козени, Л. С. Лейбензона, К. Г. Оркина и других с удельной поверхностью связан ряд других свойств пород. Так, например, при использовании уравнения (1. 49) удельная поверхность породы по ее гранулометрическому составу может быть определена по формуле

(1.50)

где Р — масса породы в кг; Рi — масса данной фракции в кг; d_i — средние диаметры фракций в м, определяемые

по формуле

, (1.50^’),

где d^’_i и д^’’_i — ближайшие стандартные размеры отверстий сит.

По экспериментальным данным К. Г. Оркина при определении дельной поверхности по механическому составу в формулу (1. 50) следует ввести поправочный коэффициент, учитывающий повышение удельной поверхности вследствие нешаровидности формы зерен, величина которого равна . Меньшие значения α отно­сятся к окатанным зернам, большие — к угловатым.

Используя уравнения, связывающие параметры фиктивного грунта, аналогичные формуле (1. 49), можно также установить за­висимость между удельной поверхностью и другими параметрами реальных пород. Для этого при выводе соответствующих формул реальный грунт с неоднородными частицами заменяют эквивалент­ным естественному фиктивным грунтом, который обладает одинако­вым гидравлическим сопротивлением фильтрации жидкости, с такой же удельной поверхностью, как и естественный грунт. Диаметр частиц фиктивного грунта, обладающего этими свойствами, принято называть эффективным (d_эф). Сопоставляя формулы (1. 49) и (1. 50), можно видеть, что

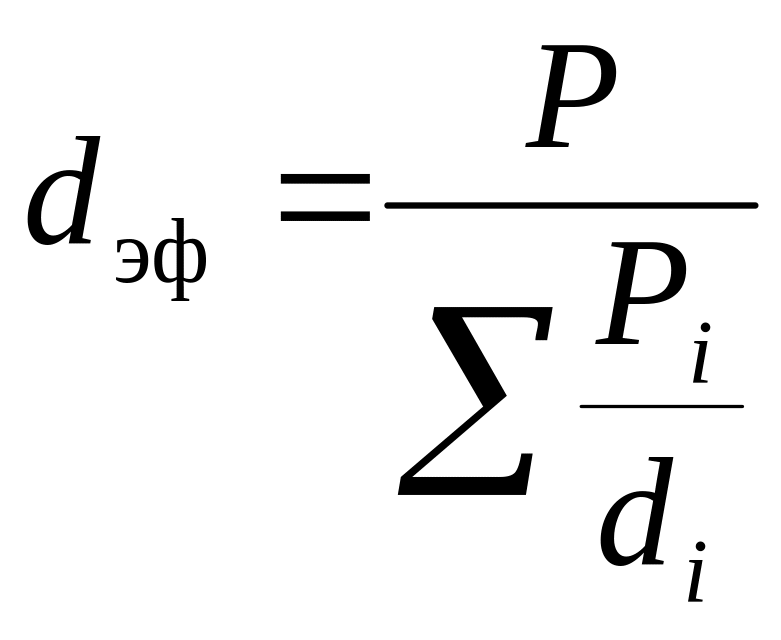, (1.51)

или

, (1.52)

С другой стороны, удельную поверхность можно выразить через гидравлический радиус δ:

или , (1.53)

Гидравлический радиус, как известно, равен отношению площади порового канала к его периметру и для поры с круглым сечением, с радиусом R

Тогда можно написать

, (1.54)

Подставляя значение R из формулы (1. 19), получи

, (1.55)

где k — проницаемость в м²; S — удельная поверхность в м²/м³. Если выразить проницаемость в дарси, то получим удельную поверхность в м²/м³:

, (1.56)

Из формул (1. 56) и (1. 54) следует, что чем меньше радиус поровых каналов и проницаемость породы, тем больше ее удельная поверхность.