8.10. Упрощенные способы вычисления средней арифметической и среднего квадратического отклонения

Основными характеристиками любого статистического исследования, когда статистический материал представлен рядами распределения, являются средняя арифметическая и среднее квадратическое отклонение. При этом следует иметь в виду, что ряды распределения получаются уже при группировке данных. Среднюю арифметическую и среднее квадратическое отклонение можно определять и по необработанным наблюдениям. В этом случае целесообразно воспользоваться упрощенными способами их расчетов (конечно, при совпадении результатов).

Пусть из анализа индивидуальных значений признака установлено начало отсчета отклонений от некоторого индивидуального значении, принятого за условное начало А. В этом случае по свойству средней арифметической имеем:

,

где - называется моментом первого порядка.

Для сгруппированных данных этот подход приводит к формуле вида:

,

где .

В некоторых случаях этот способ рекомендуется реализовать с использованием формулы:

, где .

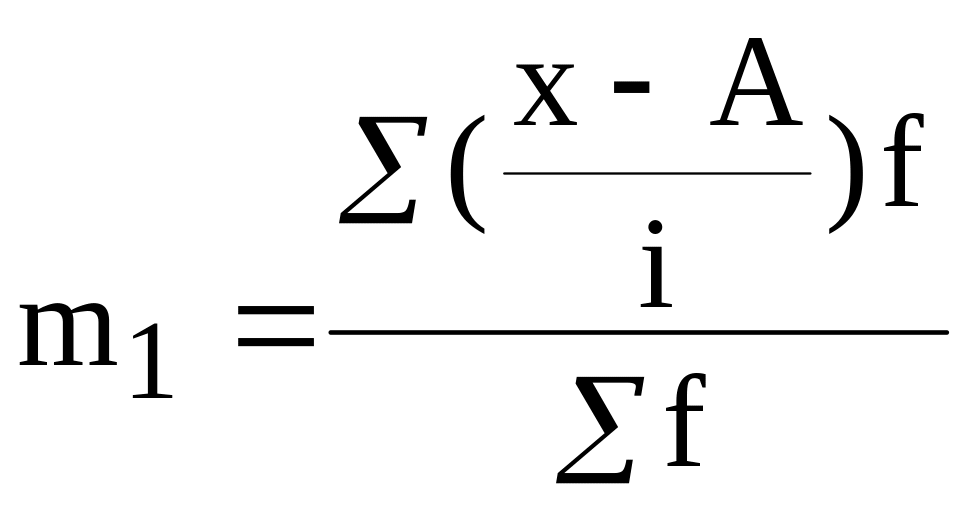В качестве А применяется обычно одна из центральных варрант ряда, если ряд имеет нечетное число единиц совокупности. При четном числе признаков берется среднее значение из двух вариант с наибольшей частотой. В качестве i берется общий (наибольший) делитель индивидуальных отклонений. В интервальном ряду в качестве i целесообразно использовать величину интервала.

Аналогичным образом можно вывести формулу упрощенного вычисления среднего квадратического отклонения:

,

т.е. , то имеем

или

.

Поскольку , то можно записать

,

где - момент второго порядка, .

Для сгруппированных данных будет применяться формула

.

В некоторых случаях исходные данные можно и целесообразнее преобразовать, используя . Тогда .

Выбор А и i аналогично как и для упрощенного вычисления средней арифметической.

При таком подходе среднее квадратическое отклонение будет упрощенно определяться по формуле

, .

Такие способы вычисления среднего арифметического и среднего квадратического отклонения получили название способа моментов или способа отсчета от условного нуля.

8.11. Основные правила применения средних в статистике

Средние, как видели в предыдущих вопросах темы, являются важнейшими обобщающими характеристиками изучаемого массового явления. Однако если при этом средние величины будут исчислены формально, без учета особенностей этих показателей, могут быть допущены сознательные или несознательные ошибки. В первом случае речь идет о фальсификации действительных свойств, закономерностей совокупности. Поэтому недопустимо ни преувеличение роли средних (некоторые авторы статистику провозглашают наукой о средних), ни приуменьшение их значения (исчисление средних просто экономит мышление при характеристике той или иной совокупности).

Некоторые требования, которые необходимо соблюдать при исчислении средних, были рассмотрены выше. Теперь обобщим и рассмотрим эти правила в определенной последовательности.

Во-первых, средние характеристики должно исчисляться на основе массового обобщения фактов и применяться к качественно однородным совокупностям.

Значения изучаемого признака формулируются под действием многочисленных разнообразных факторов, влияние которых в разных условиях проявляется по-разному (с большей или меньшей силой проявляется постоянно или случайно). Такие индивидуальные отклонения от среднего взаимно погашаются и уничтожаются при рассмотрении большого числа единиц совокупности. Значит, средняя должна относиться к явлениям одного и того же вида и базироваться на массовом обобщении фактов.

Требование качественной однородности совокупности состоит в том, то нельзя применять средние к такой совокупности, отдельные части которой подчиняются различным законам развития в отношении осредняемого признака.

Качественная однородность изучаемого является, их однородность устанавливается на основе всестороннего теоретического анализа сущности этого явления. Такой теоретический анализ должен учитывать природу явления, законы его развития, теоретическое положение науки, объектом изучения которой является данное массовое явление.

Во-вторых, средние будучи обобщающими характеристиками для совокупности в целом, затушивывают количественные различия изучаемого признака у отдельных единиц совокупности. Поскольку массовое явление находится в непрерывном развитии, даже в пределах качественно однородной совокупности количественные различия величин признака у отдельных единиц совокупности могут носить не случайный, а систематический характер.

Поэтому даже в пределах качественно однородных совокупностей, в-третьих, нередко нужно общие средние дополнять исчислением групповых средних, т.к. общие средние могут не раскрывать подлинных закономерностей изучаемого явления или процесса.

Например, изучая динамику урожайности сельскохозяйственных культур по стране необходимо учитывать различие отдельных районов по почвенным, климатическим и другим условиям. В этом случае динамика групповых средних более полно отразит закономерности изменения урожайности, чем общая средняя урожайность.

Общие средние нужно дополнять средними групповыми и в тех случаях, когда варьирующий признак существенно различается по группам или в сравнимых совокупностях может быть неодинаковая групповая структура.

В-четвертых, средние должны применяться в органической связи с группировкой.

В типологической группировке, производимой на основании количественного признака, границы, отделяющие друг от друга качественные типы, не являются произвольными. Они выбираются по таким значениям, в которых количественные изменения переходят в новое качество. Например, классификация отраслей народной хозяйстве, работников по профессиям и т.д.

В отличие от этого в группировке, имеющей целью получение вариационного ряда, величина интервалов и, значит, границы между ними могут быть вообще любыми. Правда, и в вариационном ряду, в определенных случаях, вторичная группировка может быть использована для выделения типов. Но, как правило, при построении вариационного ряда преследуется только цель характеристики количественной вариации. Поэтому интервалы группировки устанавливаются в конечном счете по усмотрению исследователя.

В условиях автоматизации статистических исследований группировка становится частью работы ЭВМ. Но при этом должны быть разработаны стандарты для количественной группировкой.

Например, при построении равных интервалов можно предположить такие стандарты:

1) интервалировка по средним квадратическим отклонениям с границами интервалов: = всего 8 интервалов;

2) то же по - всего 14 интервалов;

3) интервалы, делящие размах на 10 равных частей с границами ; ; , …, и др.

Для неравных интервалов могут быть предложены следующие стандарты:

1) геометрические интервалы: 0; а; 3а; 7а; 15а; … Здесь ширина интервала возрастает в геометрической прогрессии, но остается открытым вопрос о ширине начального интервала. Можно и здесь принять стандарт , где «b» - верхняя граница последнего правого интервала. В данном стандарте предусмотрено возрастание интервала с каждым шагом вдвое (0-а, а-3а, 3а-7а, 7а-15а, …);

2) то же но с другим возрастанием с каждым шагом и др.

В-пятых познавательные возможности метода средних становятся значительно богаче, если средние характеристики дополняются рядами распределения. Динамику средних дополняют характеристики ряда распределения по данному признаку и тем самым можно оценивать как единичные прогрессивные изменения постепенно становятся массовыми, типичными для остальных групп. Например, среднее число обслуживаемых одним рабочим станков можно дополнить группировкой рабочих по числу обслуживаемых ими станков. И можно проследить как увеличивается группа многостаночников,, как единичное достижение передовых рабочих становится постепенно массовым, типичным для остальной части рабочих.