- •Белорусский национальный технический университет
- •Задание
- •Содеражание
- •Схемы алгоритмов подпрограммы реализации временных задержек…………………………………………………………20
- •Введение
- •1. Выбор методов решения и их обоснование
- •1.1 Метод Ньютона для нахождения корня нелинейного уравнения
- •1.2 Метод решения квадратного уравнения
- •Алгоритм Горнера для вычисления значений функции
- •1.4 Понятие машинного и реального времени
- •1.5 Дискретизация времени
- •1.6 Реализация временных задержек в программе
- •1.7 Масштабирование
- •2. Разработка схем алгоритмов и программ
- •2.1 Таблица переменных
- •2.2.2 Схема алгоритма подпрограммы решения квадратного уравнения
- •3. Вывод значений функции и её коэффициентов
- •3.3. График временной функции
- •Заключение
- •Список использованных источников
1.6 Реализация временных задержек в программе
Для реализации временных задержек в программе используется таймер. Таймером определяется время квантования. В данной программе задержка реализуется путём многократного выполнения функции time = exp (0.5). Время задержки регулируется путём изменения параметров цикла.
1.7 Масштабирование
Для наглядного представления и сравнительной оценки результатов вычислений целесообразно их размещать в таблицы и представлять в виде графиков.
При размещении результатов вычислений очень удобно пользоваться оператором PRINT совместно с функцией TAB. Конечно, можно использовать и оператор LOCATE . Функция TAB и оператор LOCATE рассмотрены в предыдущих разделах.
Что касается построения графиков функций, то можно использовать графические операторы PSET и LINE. Однако при построении графиков необходимо всегда решать вопрос, связанный с масштабированием графиков. Во-первых, при построении графиков на компьютере пользователь всегда имеет дело с дискретными функциями: yn = f(ndx) или yn = f(nTk), где dx – шаг изменения аргумента; Tk – период квантования, который является тоже шагом по аргументу, которым является время t = nTk.
Необходимо всегда оценивать минимальное и максимальное значение функции: y0(min) при n=0 и yn(max) при nmax.
Кроме того, необходимо выбрать начальную точку (a, b) для построения графика, определить границы окончания графика справа и сверху, а потом рассчитать масштаб по аргументу и по функции. Для пояснения на рисунке 10.3 показан произвольный график:
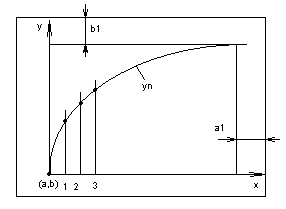
Рисунок 10.3. К выбору масштаба
Если исходить из разрешающей способности 640х480 пикселей (12 режим экрана монитора), то:
- количество пикселей по оси Х: 640 – а – а1;
- количество пикселей по оси У: b – b1,
где а1 и в1 – отступы соответственно с правой и верхней сторон экрана, как показано на рисунке 10.3.
Тогда масштабы по осям Х(Мх) и Y(Му) равны:
![]() .
.
С учетом Мх и Му координаты точек для оператора PSET будут следующими:
![]() .
.
В этих формулах учитывается, что по оси абсцисс количество пикселей возрастает при увеличении n, а количество пикселей по оси y убывает.
Для проверки правильности выбора а2 и в2 надо подставить в эти формулы значения nmax и ymax вместо n и y. При этом a2 = 640 – a1, а b2 = b1, то есть, последние значения будут соответствовать значениям отступов. Таким образом, при построении графика следует использовать PSET с координатами (a2,b2):
![]() .
.
Для возможности перемещения графика по экрану рекомендуется расчет масштабирования вводить в программу.
2. Разработка схем алгоритмов и программ
2.1 Таблица переменных
Таблица переменных программы представлена в таблице2.1
Имя переменной |
Коэффициент |
Пояснения |
|
К |
к |
Коэффициент функции |
|
L |
l |
Коэффициент функции |
|
M |
m |
Коэффициент функции |
|
A |
a |
Коэффициент квадратного уравнения |
|
B |
b |
Коэффициент квадратного уравнения |
|
C1 |
с1 |
Коэффициент квадратного уравнения |
|
Q |
q |
Корень нелинейного уравнения |
|
C |
c |
Наименьший по абсолютному значению корень квадратного уравнения: |
|
TK |
tk |
Время квантования |
|
T0,TKON |
t0, tkon |
Значения, задающие временной отрезок |
|
YMIN,YMAX |
ymin, ymax |
Минимальное и максимальное значения функции |
|
2.2 Схема алгоритма основной программы
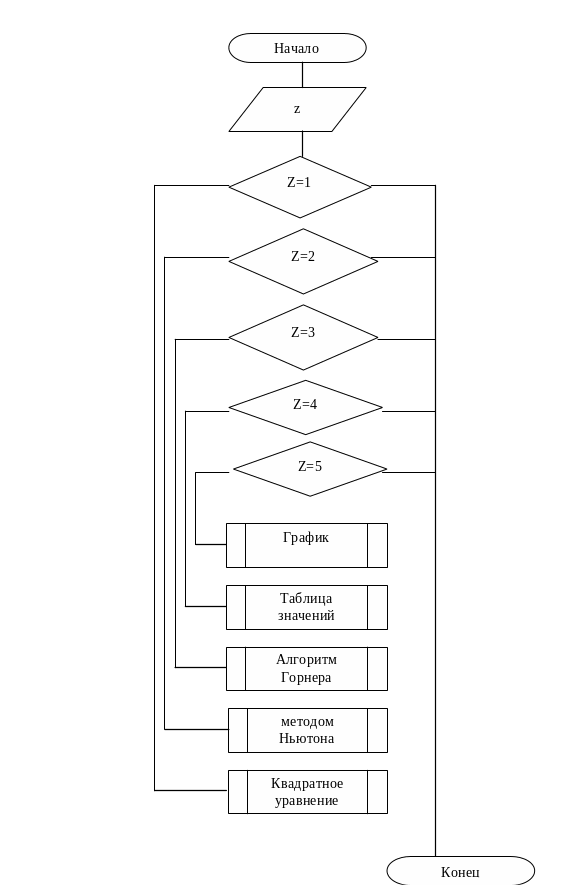
2.2 Схемы алгоритмов подпрограмм
2.2.1 Схема алгоритма подпрограммы решения нелинейного уравнения
Методам Ньютона