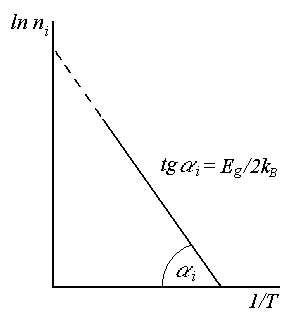12. Уровень Ферми и концентрация носителей в собственных полупроводниках

Определим положение уровня Ферми и концентрацию носителей в собственном полупроводнике в зависимости от температуры. Примем за нулевой уровень дно зоны проводимости .

При температуре абсолютного нуля валентная зона полностью заполнена электронами, зона проводимости свободна. С повышением температуры за счет термического возбуждения часть электронов переходит в зону проводимости, незанятые состояния валентной зоны ведут себя как положительные частицы – дырки. Так как электроны и дырки появляются парами, то равновесные концентрации электронов n₀ и дырок р₀ равны

. (4.113)

Это есть условие электронейтральности или условие сохранения заряда для собственного полупроводника.

Воспользуемся распределением электронов по энергиям для зоны проводимости (4.76). Так как число квантовых состояний в зоне значительно превышает долю состояний, занятых электронами, то функция . Следовательно, . Поскольку заполненными являются состояния вблизи дна зоны, то есть возле Е=0, то должно выполняться условие

. (4.114)

Это означает, что уровень Ферми собственного полупроводника располагается в запрещенной зоне, а само условие (4.114) отражает тот факт, что электронный газ в полупроводнике является невырожденным.

Определим положение уровня Ферми в полупроводнике в зависимости от температуры. Для этого проинтегрируем (4.76), заменив на бесконечность верхний предел интегрирования. Это можно сделать, так как подынтегральная функция быстро убывает с ростом Е. Используя условие (4.114), получаем

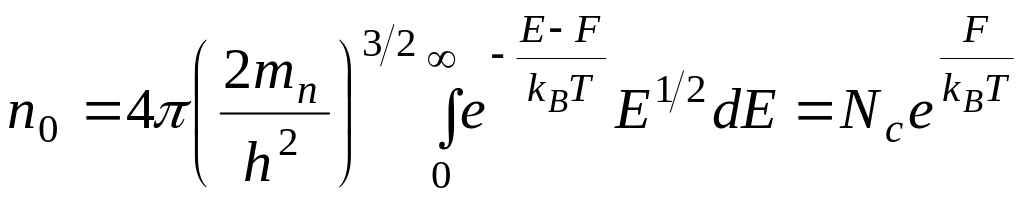, (4.115)

где под понимается эффективная масса для плотности состояний (4.108), а

коэффициент

(4.116)

называется эффективной плотностью состояний для дна зоны проводимости.

Аналогичный расчет для дырок в валентной зоне дает

(4.117)

где – положение уровня Ферми относительно потолка валентной зоны, – эффективная плотность состояний для потолка валентной зоны, которая равна

. (4.118)

Под здесь понимается эффективная масса для плотности состояний валентной зоны.

Очевидно, что

(4.119)

где – ширина запрещенной зоны полупроводника.

Воспользовавшись выражениями (4.115), (4.117), (4.119) и уравнением электронейтральности (4.113), находим положение уровня Ферми для собственного полупроводника в зависимости от температуры (рис.4.20 а):

. (4.120)

а	б
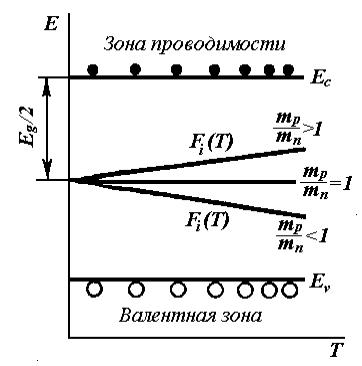
Рис.4.20. Зависимость уровня Ферми от температуры для собственного полупроводника (а) и зависимость концентрации собственных носителей от температуры (б)

При температуре абсолютного нуля и в случае, когда эффективные массы плотности состояний зоны проводимости и валентной зоны равны ( ), уровень Ферми проходит посредине запрещенной зоны. С повышением температуры уровень Ферми смещается к зоне с меньшей эффективной массой. Сдвиг это обычно малый, и только в некоторых полупроводниках, например, в , для которого , сдвиг уровня Ферми при высоких температурах может оказаться настолько значительным, что он входит в зону проводимости и электронный газ оказывается вырожденным.

Подставив F из (4.120) в (4.115), получим концентрацию собственных носителей

. (4.121)

Из (4.121) видно, что равновесная концентрация носителей в собственном полупроводнике определяется шириной запрещенной зоны и температурой полупроводника. На рис. 4.20, б приведена температурная зависимость концентрации собственных носителей заряда.