- •Структура кристаллических и аморфных тел
- •Структура кристаллов
- •Точечная и пространственная симметрия
- •Точечные группы симметрии
- •Группы пространственной симметрии
- •Решетки Браве5
- •Кристаллографические индексы. Период идентичности. Угол между кристаллографическими направлениями
- •Обратная решетка
- •Ячейки Вигнера-Зейтца7 и зоны Бриллюэна8
- •Типичные кристаллические структуры
- •Симметрия и физические свойства кристаллов
- •Анизотропия и полиморфизм твердых тел
- •Жидкие кристаллы
- •Полимеры, аморфные тела и керамика
- •Контрольные вопросы и задачи
Обратная решетка
В физике твердого тела при анализе многих явлений (дифракция рентгеновских лучей или электронов, рассеяние фотонов и т.д.) часто используют понятие обратной решетки. Для идеального монокристалла, который является трехмерным повторением некоторой структурной единицы, обратная решетка представляет собой бесконечное трехмерное распределение точек, расстояния между которыми обратно пропорциональны расстояниям между плоскостями прямой решетки. Поэтому условие брегговской дифракции может быть выражено через расстояния обратной решетки.
Поскольку
векторы в реальном пространстве имеют
размерность длины, размерность векторов
в обратном пространстве есть обратная
длина. Векторы обратного пространства
с точностью до масштабного множителя
2
можно сопоставить с волновыми векторами
возбуждений, с помощью которых в физике
твердого тела описывается движение
электронов (или любых квазичастиц) в
кристаллической решетке. Умножение
координат обратного пространства на
постоянную
![]() переводит его в пространство импульсов.
Для построения обратной решетки вводят
вектора трансляции
переводит его в пространство импульсов.
Для построения обратной решетки вводят
вектора трансляции
![]() ,
связанные с векторами трансляции прямой
решетки соотношениями
,
связанные с векторами трансляции прямой
решетки соотношениями
 ,
(1.12)
,
(1.12)
где
![]() –
объем элементарной ячейки.
–
объем элементарной ячейки.
Отметим некоторые свойства обратной решетки.
Каждый узел обратной решетки соответствует семейству параллельных плоскостей прямой решетки.
Вектор
обратной решетки
![]() является перпендикулярным к плоскости
с индексами
является перпендикулярным к плоскости
с индексами
![]() атомной решетки.
атомной решетки.
Модуль
вектора обратной решетки
![]() равняется обратному расстоянию между
ближайшими плоскостями семейства
равняется обратному расстоянию между
ближайшими плоскостями семейства
![]() :
:
![]() .
(1.13)
.
(1.13)
Если
в кристаллической решетке все углы
прямые, то векторы элементарных трансляций
![]() обратной решетки
параллельны векторам
обратной решетки
параллельны векторам
![]() прямой решетки и
обратны им по величине.
прямой решетки и
обратны им по величине.
Представление об обратной решетке оказывается очень эффективным в решении задач физики кристаллов и рентгеноструктурного анализа. Например, рентгенограмма есть взятая в некотором масштабе проекция обратной решетки кристалла.
Ячейки Вигнера-Зейтца7 и зоны Бриллюэна8
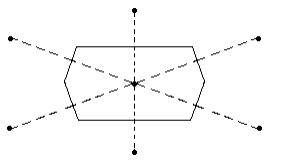
Рассмотренные выше элементарные ячейки построены в базисе Браве. Однако иногда пользуются так называемой ячейкой Вигнера-Зейтца, параллельным переносом которой можно заполнить все пространство без промежутков. Для ее построения необходимо выбрать определенный узел в начале координат. Потом соединить этот узел отрезками с ближайшими узлами и через середины отрезков провести перпендикулярные к ним плоскости, которые ограничат определенную область пространства. Этот объем и представляет собой ячейку Вигнера-Зейтца (рис. 1.14). Эта ячейка содержит только один выбранный узел, а все точки внутри нее лежат ближе к центру ячейки, чем ко второму трансляционно эквивалентному узлу.
Ячейка Вигнера-Зейтца для примитивной кубической решетки представляет собой куб, для ОЦК решетки – кубооктаэдр, для ГЦК – додекаэдр.
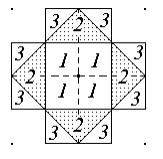
Если аналогичное построение выполнить в обратном пространстве, то образованные фигуры называют зонами Бриллюэна. Имеют место первая, вторая, третья и т.д. зоны Бриллюэна, образуемые в результате пересечения плоскостями отрезков, которые соединяют центральный узел с атомами первой, второй, третьей и т.д. координационных сфер. На рис. 1.15 показаны зоны Бриллюэна для двумерной решетки.
-
Рис.1.14. Схема построения двумерной ячейки Вигнера-Зейтца
-
Рис.1.15. Первые три зоны Бриллюэна для двумерной решетки
Для примитивной кубической (ПК) решетки первая зона Бриллюэна является также примитивной кубической, для ОЦК решетки первой зоной Бриллюэна является додекаэдр, для ГЦК решетки – кубооктаэдр. Соотношение между формами прямой решетки, обратной решетки, ячейки Вигнера-Зейтца и зон Бриллюэна для трех кубических решеток приведено в табл.1.3.
Таблица 1.3. Форма прямой решетки, обратной решетки, ячейки Вигнера-Зейтца и зон Бриллюэна для кубических решеток
Атомная решетка |
Обратная решетка |
Ячейка Вигнера-Зейтца |
Зоны Бриллюэна |
ПК |
ПК |
ПК |
ПК |
ОЦК |
ГЦК |
Кубооктаэдр |
Додекаэдр |
ГЦК |
ОЦК |
Додекаэдр |
Кубооктаэдр |
Одной
из основных задач физики твердого тела
является вычисление зависимости энергии
носителей заряда от волнового вектора
![]() ,
однако это практически невозможно
выполнить для всей зоны Бриллюэна.
Поэтому вычисление проводят вдоль
определенных направлений, которые имеют
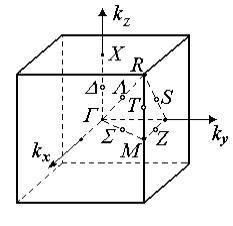
общепринятые обозначения (рис. 1.16). Центр
зоны Бриллюэна всегда отмечают буквой
,
однако это практически невозможно
выполнить для всей зоны Бриллюэна.
Поэтому вычисление проводят вдоль
определенных направлений, которые имеют
общепринятые обозначения (рис. 1.16). Центр
зоны Бриллюэна всегда отмечают буквой
![]() .
.
Не существует металлов и полупроводников с простой кубической решеткой, но она лежит в основе некоторых сплавов и соединений. Например, для - латуни и хлористого цезия. Зона Бриллюэна для электронных состояний в таких кристаллах представляет собой простой куб (рис. 1.16, а). Для характерных точек зоны используют такие обозначения:
– центр квадратной грани;
![]() –
вершина
куба;
–
вершина
куба;
![]() –
середина
ребра;
–
середина
ребра;
![]() –
середина
ребра между шестиугольной и квадратной
гранями;
–
середина
ребра между шестиугольной и квадратной
гранями;
![]() – середины
расстояний
– середины
расстояний
![]() и
и
![]() соответственно;
соответственно;
![]() – середины
расстояний
– середины
расстояний
![]() и
и
![]() соответственно.
соответственно.
Для характерных точек зоны Бриллюена ГЦК структур используют следующие обозначения (рис.1.16, б):
![]() – центр
шестиугольной грани;
– центр
шестиугольной грани;
– центр квадратной грани;
![]() –
вершина
срезанного октаэдра;
–
вершина
срезанного октаэдра;
![]() –
середина
ребра между двумя шестиугольными
гранями;
–
середина
ребра между двумя шестиугольными
гранями;
– середина ребра между шестиугольной и квадратной гранями;
– середины
расстояний
![]() и
и
![]() соответственно.
соответственно.
|
|
|
а |
б |
в |
Рис.1.16. Первые зоны Бриллюэна для простой кубической (а), ОЦК (б) и ГЦК (в) решеток Браве |
||
Обозначение точек в зоне Бриллюэна ОЦК структур приведено на рис. 1.16, в.