2.9. Распределение напряжения по длине волокон..

Анализируя прочность КМ, армированных параллельными дискретными волокнами, мы отметили, что от матрицы к волокну нагрузка передается за счет касательных напряжений τ, действующих на границе раздела. Эти напряжения, как и нормальные напряжения в волокнах, на концах волокна и в средней его части не одинаковы.

Закономерности распределения напряжений вдоль волокон. Разработано несколько моделей, позволяющих установить распределение напряжений. Приводят эти модели к качественно одинаковым результатам, поэтому мы рассмотрим только одну из них, предложенную Б. Розеном.

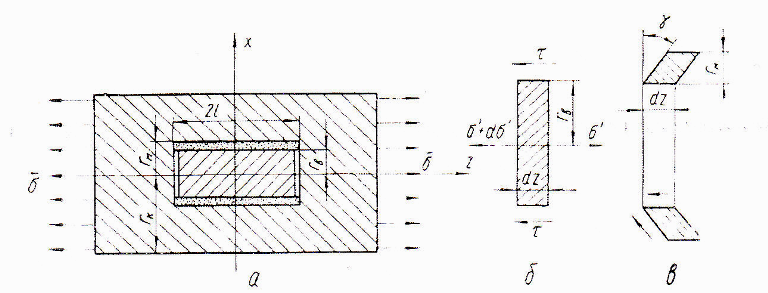
Рис. 14. К расчету распределения напряжений по длине волокна при растяжении однонаправленной композиции с дискретными волокнами: а- модель элемента КМ; б- элементарный отрезок волокна; в-элементарный отрезок матрицы в деформированном состоянии.

Модель (рис. 14,а) представляет собой волокно радиусом и длиной 2 , жестко связанное с тонким цилиндрическим слоем матричного материала радиусом , который в свою очередь окружен оболочкой радиусом из материала с осредненными свойствами композиции. Пусть ось волокна совпадает с осью z, а ось х проходит перпендикулярно к ней через середину волокна. Предполагается, что волокна несут только нормальные напряжения , а матричный слой- только касательные напряжения τ , которые в этом слое локализуются, а в оболочке с осредненными свойствами композиции отсутствуют. Нагружена модель внешним напряжением , параллельным оси волокон, при этом торцы волокна в передаче напряжений участия не принимают.

Выделим элементарный отрезок волокна длиной dz (рис. 14,б) и запишем условия равновесия сил, действующих на него. Этот отрезок нагружен касательными напряжениями τ по периферии и нормальными по торцам. Суммарная сдвиговая нагрузка, действующая на него, равна , а суммарная нормальная- . Условие равновесия запишется так:

+ =0,

или

. (1.64)

Условие равновесия сил, действующих на всю модель в направлении оси z, при условии, что матрица нормальных нагрузок не несет, можно записать в виде

,

или

, (1.65)

где -нормальное напряжение в «осредненном» КМ.

Под действием касательных напряжений τ матричный слой вместе с ним «осредненный» КМ сдвигаются по отношению к волокну. Для элементарного отрезка матрицы (рис. 14, в) величину тангенса угла сдвига можно выразить как

, (1.66)

где - осевое перемещение волокна; u – осевое перемещение «осредненного» материала.

Предположим, что волокно, матрица и «осредненный» материал деформируются упруго и, следовательно, подчиняются закону Гука. В силу малости угла γ можно считать, что , и записать

. (1.67)

Продифференцируем обе части равенства (1.67) по z, учитывая при этом известные из сопротивления материалов соотношения и , где ε- относительная деформация, Е и G – модули нормальной упругости и сдвига. Тогда получим

,

или

. (1.68)

Здесь ε и - относительные линейные деформации «осредненного» материала и волокна, соответственно; и - модули Юнга «осредненного» КМ и волокна; - модуль сдвига матрицы.

Продифференцировав еще раз по z уравнение (1.68), получаем

. (1.69)

Если продифференцируем по z уравнение (1.65), то получим

,

или

. (1.70)

Подставив в уравнение (1.69) вместо выражение (1.70), а вместо выражение (1.64), приходим к дифференциальному уравнению относительно касательных напряжений τ :

, (1.71)

где

. (1.72)

Решение уравнения (1.71) имеет вид

. (1.73)

Используя граничные условия: τ =0 при z =0 и =0 при z =l (начало координат находится в середине волокна), приходим к уравнениям, устанавливающим зависимость касательных и нормальных напряжений от координаты z:

; (1.74)

. (1.75)

Нормальные напряжения в волокне увеличиваются от концов волокна к его середине, достигая при z =0 максимального значения

. (1.76)

Касательные напряжения имеют наибольшую величину на конце волокна (при z = l) и уменьшаются до нуля в его середине (при z =0). Эпюры нормальных и касательных напряжений представлены на рис. 15.

Если принять, что , то безразмерный параметр

(1.77)

и тогда уравнения (1.74) и (1.75) можно привести к виду

(1.78)

и

, (1.79)

где - максимальное нормальное напряжение в бесконечно длинном волокне.

Если матрица проявляет пластические свойства, то концентрация касательных напряжений у концов волокна уменьшается, однако характер изменения напряжений по длине волокна остается тем же.

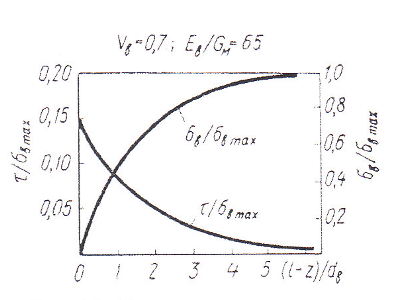
Рис.15.Распределение нормальных и касательных напряжений по длине

волокна при растяжении КМ, содержащего 70% волокон.

Неэффективная длина волокон. Поскольку нормальные напряжения у концов малы, волокна здесь оказываются недогруженными. В результате часть волокна «неэффективна» как элемент, несущий нагрузку. Длина этой части зависит от соотношения упругих свойств матрицы и волокон, от геометрических параметров модели.

Неэффективно нагруженные участки волокон имеются и при растяжении КМ с непрерывной арматурой. Обычно волокна обладают существенным разбросом прочности и часть из них разрушается даже при сравнительно низких напряжениях. У концов разрушившихся волокон напряжения распределяются примерно так же, как у концов дискретных волокон, поэтому концы сломанных волокон не создают упрочнения т.е оказываются неэффективными. Точно определить размер неэффективной части волокна нельзя: это понятие условное полезное при рассмотрении статистической модели прочности КМ.

Условимся называть неэффективной длиной волокна l* такое расстояние от его конца, на котором растягивающее напряжение в волокне достигает определенной, наперед заданной части напряжения в бесконечно длинном волокне . Иными словами, в конце неэффективного отрезка волокна

,

где φ – коэффициент, меньший 1;обычно считают разумным φ≈0,9.

Если в уравнение (1.79) положить ; и решить его относительно z (при этом z = l*), получим

. (1.80)

Чтобы волокна были нагружены эффективно (напряжение в их середине превышает 0,9 ), нужно их длину брать большей 2 l*, поскольку неэффективные участки существуют у обоих концов. Эффективный участок в этом случае – отрезок длиной L-2 l*, где L – общая длина волокна. С увеличением L эффективность армирования увеличивается. При упруго- пластическом поведении матрицы неэффективная длина волокна больше, чем при чисто упругом.