2. Обработка результатов измерений

Результаты обработки прямых (однократных и многократных, равноточных и неравноточных) и косвенных измерений следует оформлять в соответствии с рекомендациями МИ 1317. Ниже приведена методика обработки прямых многократных равноточных измерений , представляющая собой совокупность следующих этапов:

− исключение из результатов измерений известных систематических погрешностей;

− вычисление выборочного среднего (среднего арифметического) значения ͞x измеряемой величины из n одинаковых результатов;

− вычисление средней квадратической погрешности единичных измерений в ряду измерений S ;

− исключение промахов (грубых погрешностей измерений);

− вычисление средней квадратической погрешности результата измерения выборочного среднего S ͞x;

− проверку гипотезы о принадлежности результатов измерений нормальному закону;

− вычисление доверительных границ случайной погрешности результата измерений ± ε;

− вычисление доверительных границ неисключенной систематической погрешности результата измерений ± θ;

− вычисление доверительных границ погрешности результата измерений

± (Δ х)_Σ ;

− представление результата измерения в виде X = ͞x ± (Δ х)_Σ ,P;

где: P − доверительная вероятность.

Известные систематические погрешности исключают введением в результат измерений соответствующих поправок, численно равных систематическим погрешностям, но противоположным им по знаку. Поправку вводят в результаты единичных измерений, а если известно, что результаты всех единичных измерений имеют одинаковые систематические погрешности, ее исключают из среднего арифметического значения измеряемой величины.

Среднее арифметическое значение измеряемой величины из n

единичных результатов х определяют по формуле:

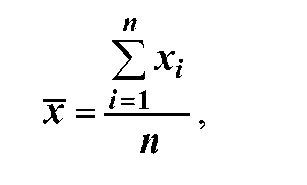
(1)

где х_i - результат i-го единичного измерения из ряда многократных измерений; n - чис ло измерений в ряду многократных измерений. Для определения средней квадратической погрешности единичных изме­рений в ряду измерений используют формулу:

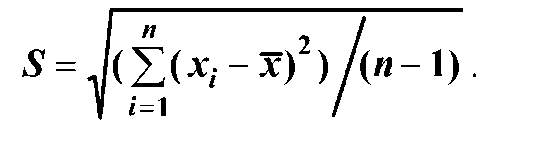
(2)

Промахи (грубые погрешности измерений) могут сильно исказить резуль­тат измерений, поэтому их исключение из ряда измерений обязательно. Суще­ствует несколько критериев для оценки промахов [8, 9]. При числе измерений n < 20 целесообразно применять критерий Романовского [9]. При этом вычис­ляют отношение:

(3)

где х_пр - проверяемый сомнительный результат измерения. Полученное значение β сравнивают с теоретическим значением β_т (табл. 1), определенным для установленного уровня значимости q; (q = 1 - P).

Таблица 1

Значения β_т=f(n,q)

Уровень значимости q	Число измерений n
	4	6	8	10	12	15	20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,69	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

При β ≥ β_т результат измерения х_пр исключают («отбрасывают»»), так как он является промахом. Если число измерений невелико (n < 10), можно использовать критерий Шовине.

В этом случае считают, что результат х_i = х_пр является промахом, если │͞x - x_пр│ превышает значения, приведенные ниже.

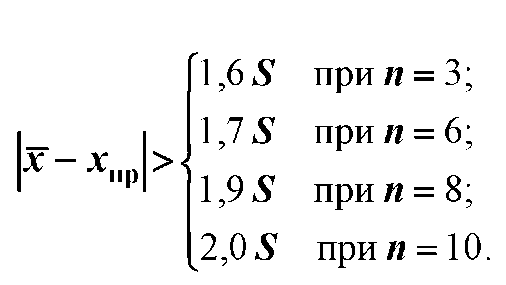
(4)

Пример 1. При измерении размера детали микрометром были получены значения: 12,24; 12,26; 12,28; 12,28; 12,31; 12,34; 12,40; 12,41; 12,42; 12,42; 12,45; 12,80 мм. Число измерений n = 12. Последний результат (12,80 мм) вы­зывает сомнения. Принимаем Р = 0,95, тогда q = 0,05.

Выполнив расчеты, получили значения ͞x = 12,38 мм; S=0,15 мм. Так

как n < 20 для определения промахов используем критерий Романовского, опре­делив его по формуле (3):

Для n =12 и q = 0,05 β_т=2,52 (см. табл.2). Т.е. β> β_т и результат

x_i = х_пр = 12,80 мм необходимо «отбросить», как промах.

После исключения результатов, содержащих промахи, определяют но­вые значения х и S и, если есть сомнения, процедуру проверки наличия прома­хов повторяют.

Пример 2. При измерении диаметра вала микрометром были получены значения: 30,12; 30,27; 30,28; 30,29; 30; 32; 30,38 мм. Число измерений n = 6.

Первый результат (30,12 мм) вызывает сомнения.

Выполнив расчеты, получили значения ͞x = 30,28 мм; S =0,086 мм. Так как n < 10, для определения промахов используем критерий Шовине:

│͞x - x_пр│=│30,28 – 30,12│ = 0,16 мм,

что больше, чем 1,7 S = 0,146 мм. Следовательно, причиной появления резуль­тата x_i = х_пр = 30,12 мм является промах и этот результат необходимо ис­ключить из полученного ряда результатов измерений.

Далее вычисляют среднюю квадратическую погрешность измерений среднего арифметического

(5)

При заданном значении доверительной вероятности Р и числе единичных измерений n по таблицам (например, по табл. 2) определяют коэффициент Стьюдента t.

Таблица 2.

Значения коэффициента Стьюдента t (ГОСТ 8.207)

P	n
	2	3	4	5	6	7	8	9	10	15
0,95	12,706	4,303	3,182	2,776	2,571	2,447	2,365	2,306	2,262	2,145
0,99	63,657	9,925	5,841	4,604	4,032	3,707	3,499	3,355	3,250	2,977

При нормальном законе распределения результатов измерений доверительные границы (величину) случайной погрешности результата измерений определяют по формуле

(6)

Доверительные границы неисключенной систематической погрешности измерения, если можно выделить ее составляющие θ_i, определяют по формуле

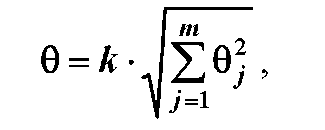
(7)

где к - коэффициент (табл. 4), определяемый принятой доверительной вероят­ностью P и числом m составляющих неисключенной систематической погрешности; θ_j - границы j-ой составляющей этой погрешности.

Таблица 4.Значения коэффициента к (ГОСТ 8.207)

P	m
	5 и более	4	3	2
0,95	1,1
0,99	1,45	1,40	1,30	1,20

Доверительную вероятность для вычисления границ неисключенной сис­тематической погрешности принимают той же, что и при вычислении довери­тельных границ случайной погрешности результата измерения.

В соответствии с ГОСТ 8.207, суммирование неисключенной системати­ческой и случайной погрешностей измерения осуществляют по следующим правилам:

1. Если отношение , то неучтенной систематической погрешностью по сравнению со случайной погрешностью пренебрегают и принимают, что доверительные границы погрешности результата измерения

Погрешность, возникающая из-за пренебрежения одной из составляющих погреш­ности, не превышает 15 %.

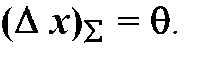2. Е сли отношение т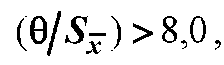 о случайной погрешностью по сравне­нию с неучтенной систематической пренебрегают и принимают, что довери­тельные границы погрешности результата измерения

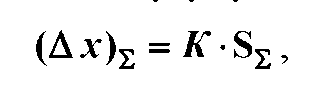3. Е сли т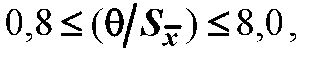 о доверительные границы погрешности ре­зультата измерения вычисляют по формуле

(7)

где К - коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешности; - суммарная средняя квадратическая по­грешность результата измерения:

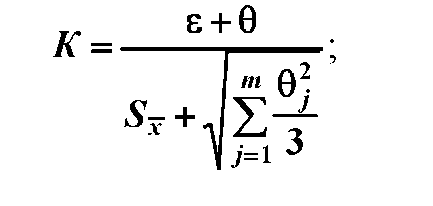
(8)

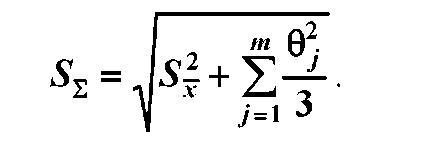
(9)

Если составляющие неисключенной систематической погрешности не ус­тановлены, а величина S соизмерима с абсолютным значением погрешности СИ , то эту величину считают неисключенной систематической погрешностью и в качестве доверительных границ погрешности результата измерений прини­мают величину

(10)

О кончательный результат записывают в виде выполняя

округление результатов расчета по правилам, изложенным в разделе 3.

Пример 3. В процессе обработки результатов прямого многократного измерения получили данные: при доверительной вероятности Р = 0,99. Результат измерения записываем в виде Х = 42,01 ±0,01, 0,99.

При отсутствии данных о законах распределения погрешностей измере­ния результат измерения представляют в виде:

(11).