Лекция 4. Дискретизация сигнала и спектра

Преобразование Фурье и его свойства. Спектральная плотность. Дискретизация и квантование. Алгоритмы ДПФ и БПФ. Теорема Котельникова. Дискретизированный сигнал и его спектр.

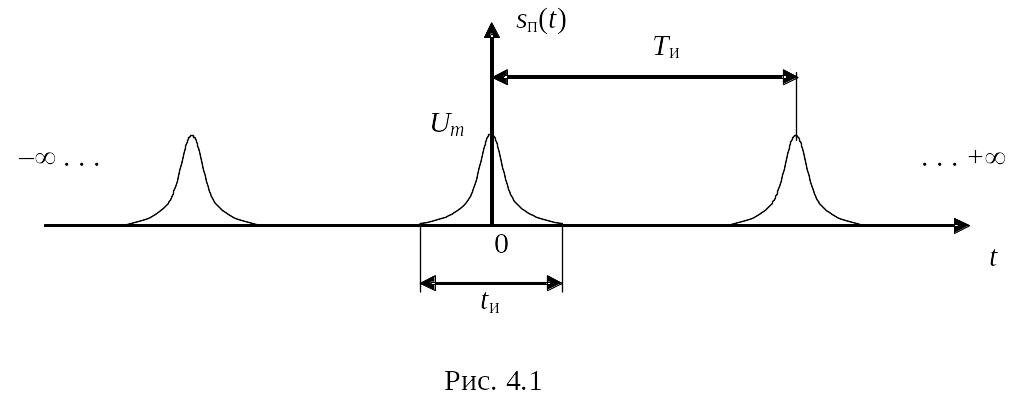
Пусть имеется произвольный периодический сигнал s_п(t) причем время задано в пределах от – до + (рис. 4.1).

Рассмотрим предельный переход

= s(t).

Преобразовав выражения (3.5), учитывая, что при Т_и   , nf₀  f ,    получим

A(f) = ,

B(f) = . (4.1)

Введем комплексную функцию

= A(f) –i B(f) = . (4.2)

Величина носит название спектральной плотности одиночного сигнала s(t).

Воспользовавшись теоремой Эйлера

e^–i = cos  – i sin ,

преобразуем (4.1) и (4.2) так

= = F[s(t)]. (4.3)

Непериодический сигнал при этом будет равен

s(t) = = F^–1[ ]. (4.4)

Выражения (4.3) и (4.4) носят название "прямое и обратное преобразование Фурье" (в литературе встречается также термин интеграл Фурье).

Физический смысл спектральной плотности состоит в распределении энергии сигнала вдоль частотной оси: на каких-то интервалах плотность энергии больше, а где-то меньше. Размерность модуля спектральной плотности – Вс, т.е. В/Гц.

Перечислим основные свойства преобразования Фурье.

1. Свойство линейности (теорема наложения, принцип суперпозиции):

F[as₁(t) + bs₂(t)] = aF[s₁(t)] + bF[s₂(t)]. (4.5)

Иными словами спектральная плотность суммы равна сумме спектральных плотностей слагаемых. С проявлением этого свойства мы уже встречались, рассматривая пример 3.5.

2. Свойство симметрии (теорема двойственности, дуальность времени и частоты):

= , (4.6)

т.е. для вещественного сигнала спектральная плотность является четной функцией.

3. Теорема о центральной ординате

S(f=0) = . (4.7)

Значение ординаты спектральной плотности на нулевой частоте численно равно "площади" сигнала.

4. Свойство инвариантности к смещению (теорема запаздывания):

F[s(t–t₀)] = S(f)exp (–i2f t₀). (4.8)

Следствие: при изменении начала отсчета времени амплитудный спектр сигнала остается неизменным, изменяется только фазовый спектр.

5. Свойство неинвариантности к масштабированию (теорема об изменении масштаба):

F[s(t)] = S( ). (4.9)

При "сжатии" сигнала (>1) спектр расширяется, амплитуда составляющих уменьшается. При "растяжении" сигнала (<1) спектр сужается, амплитуда спектральных составляющих увеличивается.

6. Теорема о дифференцировании:

F[ ] = i2f . (4.10)

7. Теорема об интегрировании

F[ ] = /( i2f). (4.11)

8. Теорема о произведении:

F[s₁(t)s₂(t)] = F[as₁(t) + bs₂(t)] = F[s₁(t)] * F[s₂(t)], (4.12)

где значком "*" обозначена операция свертки функций (см. формулу (2.6)).

Преобразование Фурье от произведения двух сигналов равно свертке спектральных плотностей.

9. Теорема о свертке

F[s(t) * h(t)] = F[s(t)] F[h(t)]. (4.13)

Преобразование Фурье от свертки двух функций равно произведению их Фурье-образов.

10. Теорема Парсеваля

= . (4.14)

Другими словами энергия сигнала равна энергии спектра.

Перечисленные свойства позволяют существенно упростить спектральный анализ сигналов.

Рассмотрим несколько примеров.

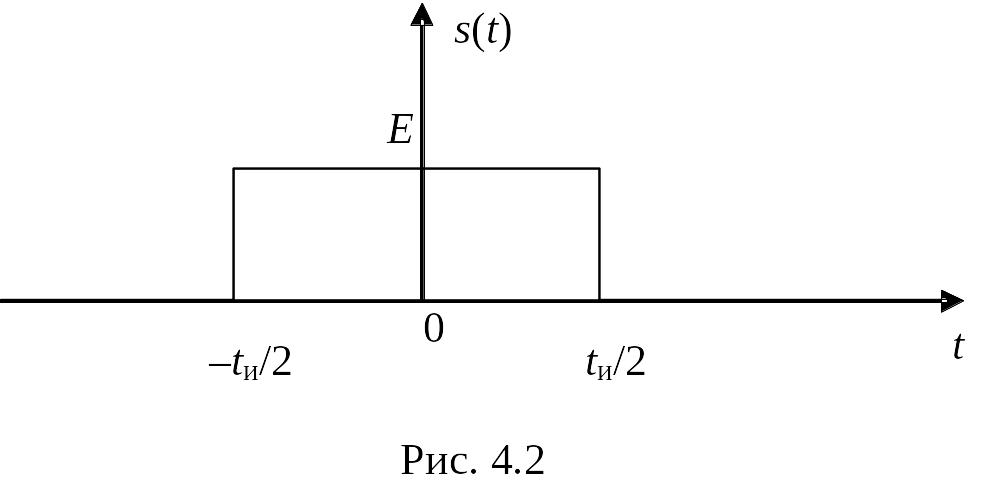
Пример 4.1. Пусть имеется сигнал в виде одиночного импульса прямоугольной формы, причем начало отсчета времени соответствует середине импульса (рис. 4.2). Найдем его спектральную плотность.

Поставим выражение для сигнала в формулу (4.3):

= = = =

= = = E/f sin (ft_и) =

= Et_и sinс (ft_и).

График спектральной плотности приведен на рис. 4.3. Как видим для четной функции получился чисто вещественный спектр, что соответствует свойству 2.

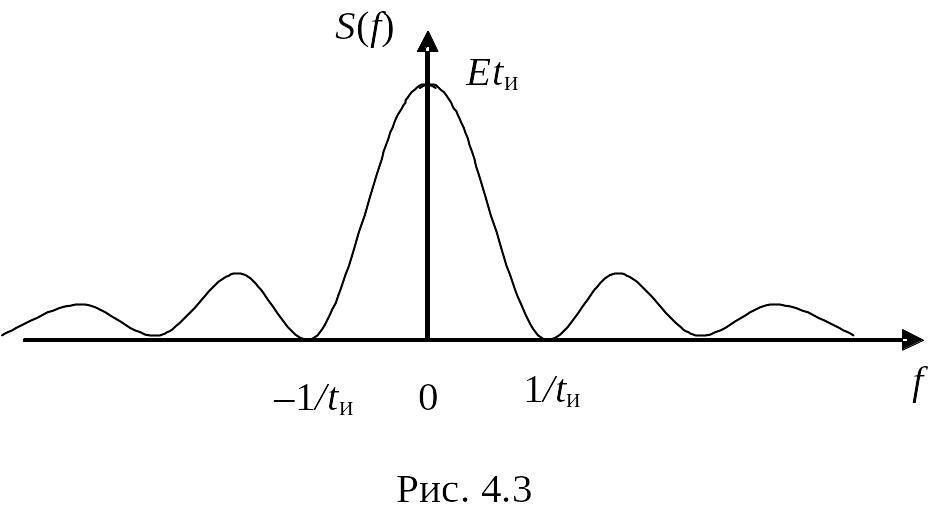
Примечание. График спектральной плотности на рис. 4.3 симметричен относительно оси ординат (слева находится область отрицательных частот). Отрицательные частоты не имеют физического смысла, их появление – следствие комплексного характера спектральной плотности. При переходе от комплекснозначной функции к вещественной компоненты, располагающиеся в левой полуплоскости, суммируются с компонентами в правой полуплоскости.

Пример 4.2. Рассмотрим односторонний экспоненциальный импульс (рис. 4.4).

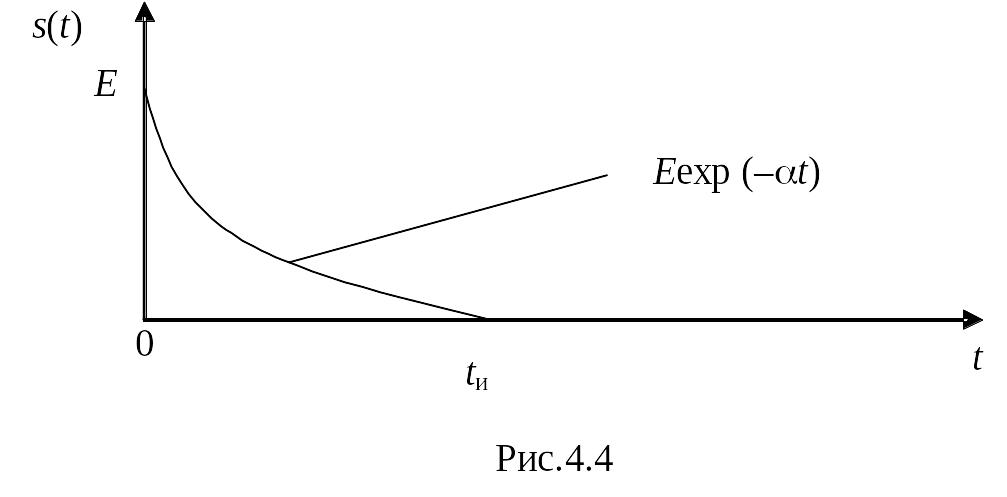
Вычисление спектральной плотности осуществляем аналогично предыдущему примеру:

= = = =

= – i .

Таким образом, несимметричный сигнал имеет комплексную спектральную плотность, состоящую из вещественной и мнимой частей.

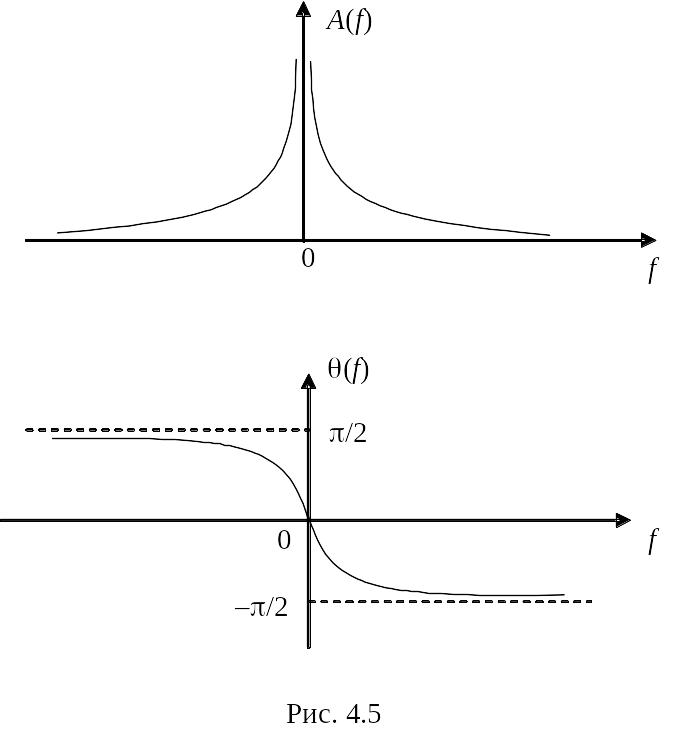
Поскольку спектральная плотность комплексная, то для ее графического представления следует выделить модуль и аргумент:

= A(f) – спектр амплитуд;

arg{ } = –arctg(2f /) = (f) – спектр фаз.

Графики амплитудного и фазового спектров приведены на рис. 4.5.

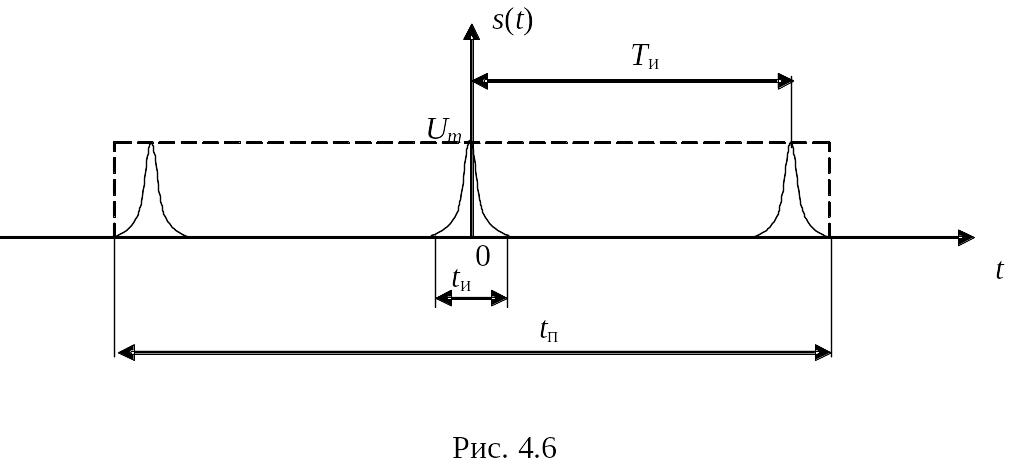
Пример 4.3. Сигнал представляет собой одиночную пачку с прямоугольной огибающей длительностью t_п, состоящую из трех гауссовых импульсов длительностью t_и, следующих с интервалом Т_и (рис. 4.6).

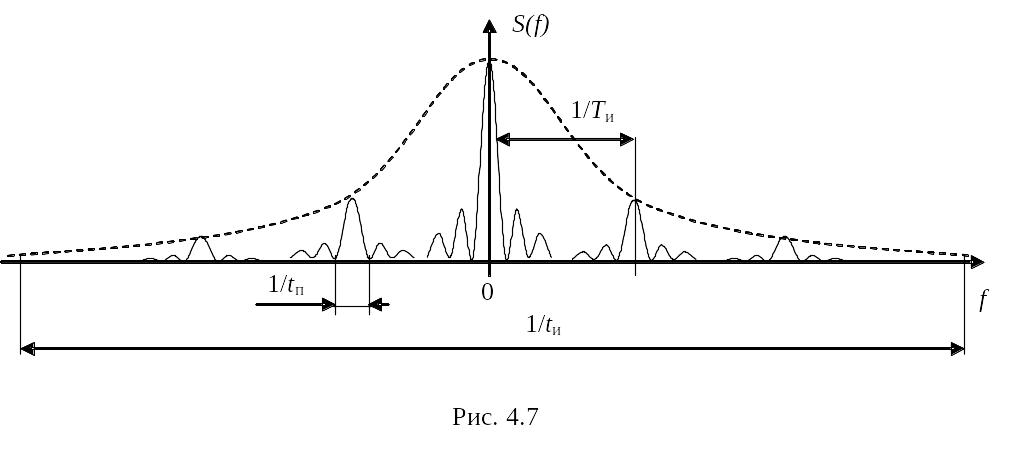
При построении спектральной диаграммы учтем то обстоятельство, что гауссовому сигналу вида ₁exp(–₁t ²) в частотной области соответствует тоже гауссова функция, но отличающаяся масштабом: ₂exp(–₂ f ²).

Второе эмпирическое правило, помогающее получить спектр данного сигнала, состоит в том, что при переходе от времени к частоте огибающей исходного сигнала будет соответствовать заполнение спектральной диаграммы, а заполнению сигнала – огибающая спектра.

Огибающая сигнала – прямоугольная функция длительностью t_п. Ее спектральная плотность была получена в примере 4.1 – это функция sinc. Поскольку интервал t_п велик, то согласно свойству 5, ширина функции sinc будет мала.

Заполнение – гауссовы импульсы – порождает такую же функцию в области частот. Длительность гауссовых импульсов мала, следовательно, ширина гауссовой огибающей будет большой.

Окончательно, амплитудный спектр будет выглядеть так, как показано на рис. 4.7.

Операции дискретизации и квантования уже упоминались в лекции 2. Рассмотрим их подробнее.

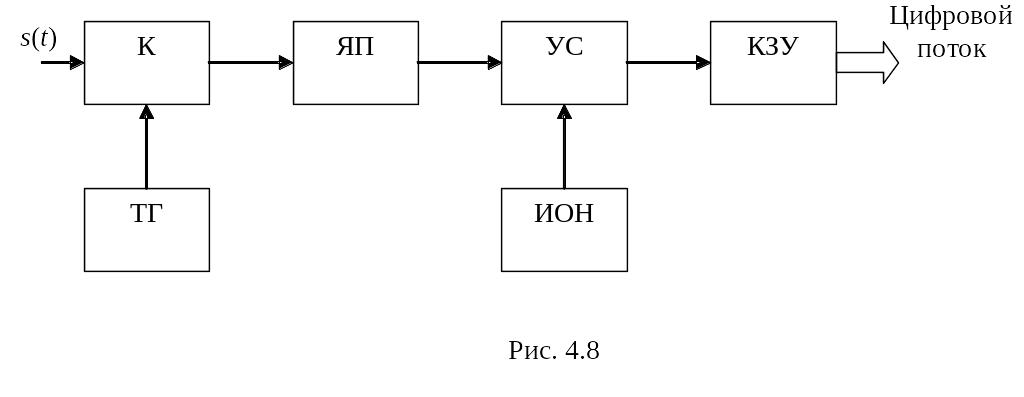
Упрощенная структурная схема аналого-цифрового преобразователя, осуществляющего дискретизацию и квантование, приведена на рис. 4.8.

Входной аналоговый сигнал поступает на коммутатор (К) управляемый от тактового генератора (ТГ), выборка сигнала запоминается в ячейке памяти (ЯП) и поступает на устройство сравнения (УС), сюда же подается эталонное напряжение от источника опорных напряжений (ИОН). В зависимости от результата сравнения соответствующий разряд устанавливается в логический ноль или логическую единицу. Далее цифровой код поступает в кодирующее и запоминающее устройство (КЗУ) и на выход АЦП в виде цифрового потока данных.

В дальнейшем цифровой поток может быть обработан в соответствии с необходимыми алгоритмами в цифровом процессоре.

Подобная схема позволяет выполнять преобразование сигналов и спектров по специально разработанным алгоритмам дискретного и быстрого преобразования Фурье (ДПФ и БПФ), а также дискретной свертки (ДС) подробнее см. в [2].

Не вдаваясь в детали, отметим, что указанные алгоритмы позволяют существенно уменьшить необходимый объем вычислений и тем самым повысить быстродействие систем обработки сигналов.

Характерной особенностью цифровых методов обработки сигналов является их дискретный характер.

Анализ дискретных сигналов и спектров базируется на фундаментальной теореме отсчетов, сформулированной в разное время независимо друг от друга Е. Уитеккером, Х. Найквистом и В.А. Котельниковым и обобщенной К. Шенноном.

Приведем формулировку теоремы, данную В.А. Котельниковым.

Пусть имеется сигнал s(t), спектр которого ограничен максимальной частотой f_max. Тогда при дискретизации этого сигнала последовательностью бесконечно коротких импульсов с интервалом

t = 1/2f_max (4.15)

потерь информации при восстановлении дискретизированного сигнала на приемной стороне не происходит.

Для иллюстрации этого рассмотрим дискретизированный сигнал и его спектр. Для упрощения спектральных преобразований в качестве огибающих сигнала (и соответственно спектра) примем гауссовы функции.

На рис. 4.9 слева показан идеальный случай дискретизации бесконечно короткими -функциями. На рис. 4.10 – реальный случай, сигнал, дискретизированный последовательностью коротких прямоугольных импульсов.

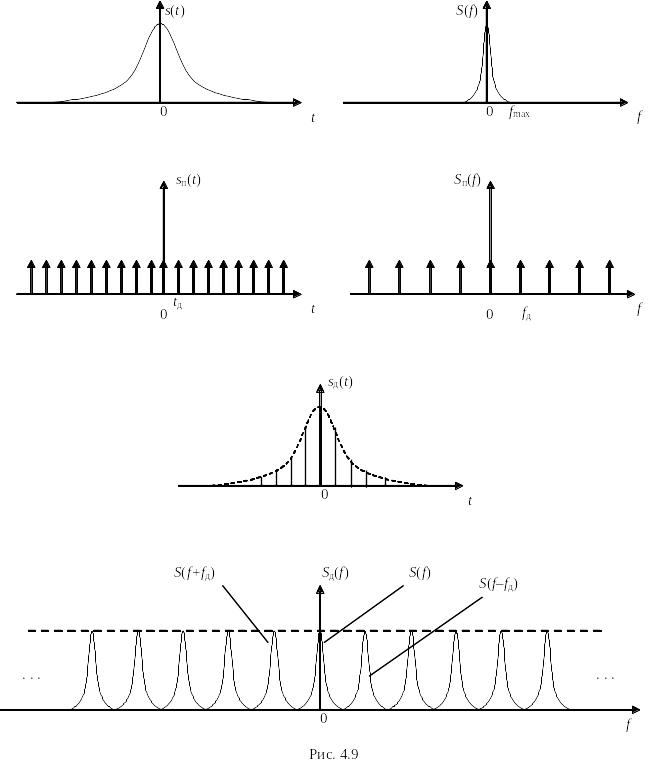
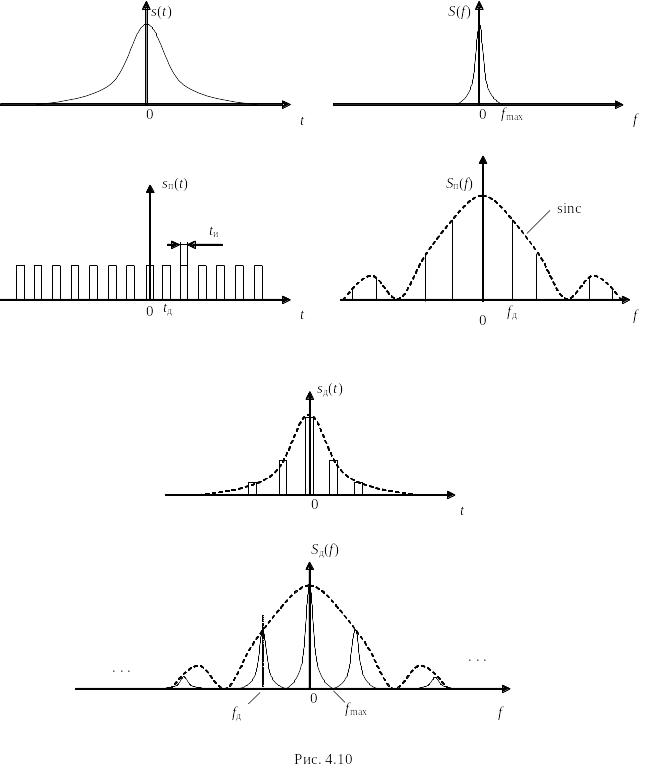
Анализируя рис. 4.9 и 4.10 можно сделать следующие выводы:

1. Спектр дискретизированного сигнала состоит из клонированных спектров исходного сигнала, он периодичен, причем период повторения по частоте равен величине, обратной интервалу дискретизации по времени.

2. В идеальном случае амплитуда клонированных спектров остается неизменной, в действительности она уменьшается с ростом частоты.

3. При точном выполнении условия теоремы Котельникова, точки смыкания первичных и вторичных спектров на частотной оси совпадают, поэтому при восстановлении сигнала с помощью идеального ФНЧ потерь информации не происходит.

4. На практике возможно перекрытие спектров и приходится нарушать т. Котельникова (4.15), вводя защитный интервал по частоте (уменьшая период следования дискретизирующих импульсов): t_д = .

5. Восстановление дискретизированного сигнала целесообразно проводить в области, близкой к нулю частот, где сосредоточена бóльшая часть его энергии.

Иногда теорему отсчетов рассматривают как интерполяционную формулу. В этом случае говорят о разложении некоторой функции по ортогональному базису функций sinc.

В области времени получим разложение вида

s(t) =  s(nt) sinc[ f_max(t – nt)].

В такой интерпретации теорема отсчетов справедлива и для дискретизированных спектров:

S(f) =  S(nf) sinc [ t_max(f – nf)].

Попутно заметим, что дискретному сигналу соответствует периодический спектр (см. рис. 4.9 и 4.10), а дискретному спектру будет соответствовать периодический сигнал (см. рис. 3.9, 3.10). Таким образом, при переходе от временного представления к частотному дискретизация всегда порождает периодичность.

Еще одну взаимосвязь временных и спектральных характеристик сигналов иллюстрирует теорема Винера – Хинчина:

K() = = F^–1[W(f)];

W(f)= = F[K()]. (4.16)

Здесь K() – АКФ сигнала, W(f) – его энергетический спектр.

Теорема справедлива не только для детерминированных, но и для случайных сигналов.