12. Электростатическое поле, его характеристики е и φ., закон Кулона, принцип суперпозиции

Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами. Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами

При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

• результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

13. Потенциальный характер электростатического поля. Связь е и φ

В электростатике работа по замкнутому контуру (циркуляция) равна нулю (не существует вечный двигатель 1 рода), тогда работа по перемещению заряда из точки 1 в 2, определяется однозначно, и не зависит от пути перемещения. Поэтому каждую точку можно характеризовать не только силой – вектором напряженности Е, но и энергетической – потенциалом поля V или ф.

14. Элементы теории поля: градиент, дивергенция, ротор, поток вектора, циркуляция вектора

Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины  , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении

дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.

Определение дивергенции выглядит так:

Введем символический вектор  . Его называют оператором Гамильтона.

Ротором вектора   называется вектор

.

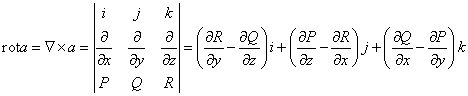Таким образом, можно сказать, что ротор вектора   равен векторному произведению символического вектора (оператора Гамильтона) на вектор  .

15. Теорема Остроградского-Гаусса для электростатического поля в интегральном и дифференциальных видах (вывод). Уравнение Пуассона

Теорема Гаусса: поток электрической индукции через любую замкнутую поверхность равен алгебраической сумме всех зарядов, находящихся внутри поверхности:  .

16. Применение теоремы Остроградского – Гаусса к расчёту поля равномерно заряженной, бесконечно длинной нити и равномерно заряженного по объёму шара, поле сферы

Расчёт напряжённости поля бесконечной нити

Рассмотрим поле, создаваемое бесконечной прямолинейной нитью с линейной плотностью заряда, равной  . Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии   от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом   и высотой  . Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицахСИ):

В силу симметрии

1. вектор напряженности поля направлен перпендикулярно нити, прямо от нее (или прямо к ней).

2. модуль этого вектора в любой точке поверхности цилиндра одинаков.

Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом:

Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю (вследствие направления E по касательной к ним). Приравнивая два полученных выражения для  , имеем: