Содержание

Глава 1. История комплексных чисел………………………………2

Глава 2. Формы комплексных чисел………………………………4

Глава 3. Формула Муавра………………………………………………7

Список использованной литературы……………………………..9

Глава 1. История комплексных чисел

Теория комплексных чисел развивалась медленно. Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), который счёл их непригодными к употреблению. Первым, кто достойно оценил комплексные числа, был итальянский математик Рафаэль Бомбелли. Именно он первым описал простейшие правила действий с комплексными числами. Выражения вида, появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках, однако даже для многих крупных ученых XVII века алгебраическая и геометрическая сущность мнимых величин представлялась неясной. Лейбниц, например, писал: «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы».

Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным результатам, или, например, извлечение корня может привести к открытию какого-то нового типа чисел. Задача о выражении корней степени из данного числа была решена в работах Муавра (1707) и Котса (1722).

Символ предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова лат. imaginarius. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришел д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.

Ещё в 18 веке крупнейшие математики мира спорили о том, как находить логарифмы комплексных чисел. Тогда с помощью комплексных чисел удалось получить много важных фактов, относящихся к действительным числам, но самое существование комплексных чисел многим казалось сомнительным. Исчерпывающие правила действий с комплексными числами дал и в 18 веке русский академик Эйлер – один из величайших математиков всех времён и народов. На рубеже 18 и 19 веков было указано Весселем (Дания) и Арганом (Франция) геометрическое изображение комплексных чисел. Но на работы Весселя и Аргана не обратили внимания, и лишь в 1831 г. когда тот же способ был развит великим математиком Гауссом (Германия), он стал всеобщим достоянием.

Слово комплекс (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д., образующих единое целое. В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование. Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а за тем из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавра (1707): с помощью этой формулы можно было так же вывести формулы для косинусов и синусов. Также применял комплексные числа для решения интегралов швейцарский математик Я. Бернулли В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие уравнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде.

В течение XVIII века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел. Поэтому французский ученый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, - только наведение, приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами синусов кратных дуг.

В конце XVIII века, в начале XIX века было получено геометрическое истолкование комплексных чисел. Датчанин К. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изобразить комплексное число точкой на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой M, а вектором, идущим 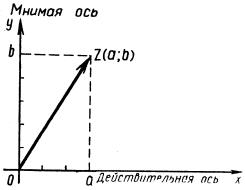в эту точку из начала координат.

Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения.

Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с величинами, которые изображаются векторами на плоскости: при изучении течения жидкости, задач теории упругости.

После создания теории комплексных чисел возник вопрос о существовании “гиперкомплексных” чисел - чисел с несколькими “мнимыми” единицами. Такую систему вида, где построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”. Тогда кватернион можно записать в виде: