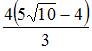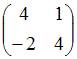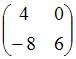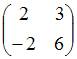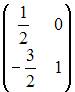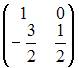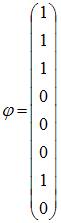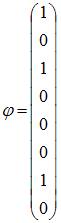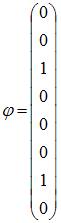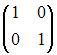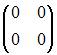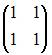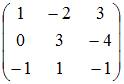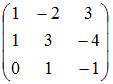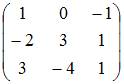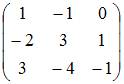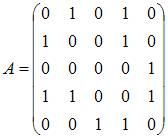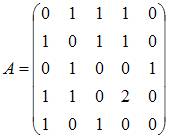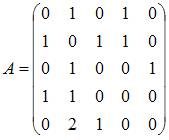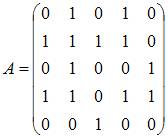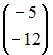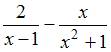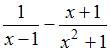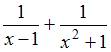Математика i-exam вариант 1
![]() ЗАДАНИЕ
N 1
Тема:
Проверка статистических гипотез
ЗАДАНИЕ
N 1
Тема:
Проверка статистических гипотез
Соотношением
вида
![]() можно
определить …
можно
определить …
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
ЗАДАНИЕ N 2 Тема: Элементы корреляционного анализа
При
построении выборочного уравнения парной
регрессии вычислены выборочный
коэффициент корреляции
![]() и
выборочные средние квадратические
отклонения
и
выборочные средние квадратические
отклонения
![]() .
Тогда выборочный коэффициент регрессии
.
Тогда выборочный коэффициент регрессии
![]() на
на
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 3 Тема: Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема
![]() ,
гистограмма частот которой имеет
вид:
,
гистограмма частот которой имеет
вид:
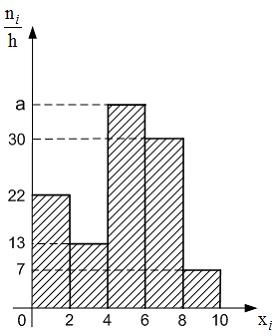 Тогда
значение a
равно …
Тогда
значение a
равно …
|
|
|
38 |
|
|
|
39 |
|
|
|
76 |
|
|
|
37 |
![]() ЗАДАНИЕ
N 4
Тема:
Интервальные оценки параметров
распределения
ЗАДАНИЕ
N 4
Тема:
Интервальные оценки параметров
распределения
Дан
доверительный интервал
![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при уменьшении объема
выборки этот доверительный интервал
может принять вид …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при уменьшении объема
выборки этот доверительный интервал
может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Доверительный
интервал для оценки математического
ожидания нормально распределенного
количественного признака можно
представить в виде симметричного
интервала
![]() ,
где точечная оценка математического
ожидания
,
где точечная оценка математического
ожидания
![]() ,
а точность оценки
,
а точность оценки
![]() .
В случае уменьшения объема выборки
точность оценки ухудшается, то есть
значение
.
В случае уменьшения объема выборки
точность оценки ухудшается, то есть
значение
![]() будет
больше 2,13.
будет
больше 2,13.

ЗАДАНИЕ N 5 Тема: Операции над высказываниями
Из
трех логических выражений:
![]()
![]()
![]() эквивалентными
являются …
эквивалентными
являются …
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
все функции |
ЗАДАНИЕ N 6 Тема: Элементы комбинаторики
Из
города
![]() в
город
в
город
![]() ведут
5 дорог, из
в
ведут
5 дорог, из
в
![]() –
3 дороги, имеются также 2 дороги из
в
,
минуя
.
Из
в
можно
попасть ____ способом(-ами).
–
3 дороги, имеются также 2 дороги из
в
,
минуя
.
Из
в
можно
попасть ____ способом(-ами).
|
17
|
|
Решение:
Из
города
в
город
можно
попасть
![]() способами,
из
в
–
с помощью
способами,
из
в
–
с помощью
![]() способов.
Тогда из
в
через
можно
попасть
способов.
Тогда из
в
через
можно
попасть
![]() способами
(по правилу произведения); а из
в
,
минуя
,
можно попасть
способами
(по правилу произведения); а из
в
,
минуя
,
можно попасть
![]() способами.
Поэтому
по правилу суммы общее число способов,
которыми можно попасть из города
в
город
,
равно:
способами.
Поэтому
по правилу суммы общее число способов,
которыми можно попасть из города
в
город
,
равно:
![]() .
.
ЗАДАНИЕ N 7 Тема: Декартово произведение множеств
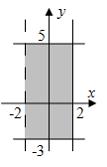
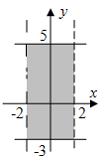
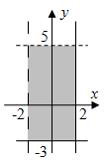
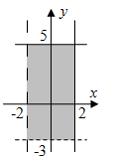
Пусть
заданы два множества:
![]() ,
,
![]() .
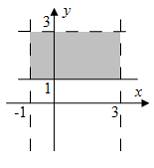
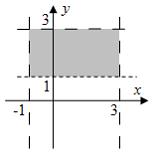
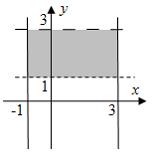
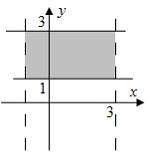
Тогда
геометрическая интерпретация множества
.
Тогда
геометрическая интерпретация множества
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 8 Тема: Неориентированные графы
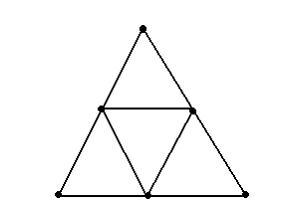
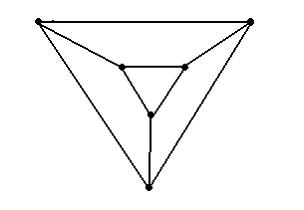
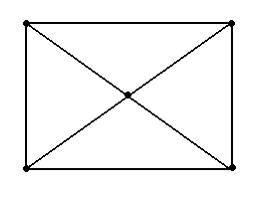
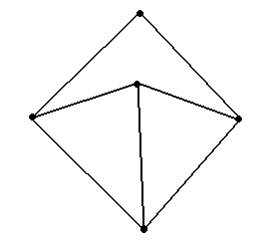
Эйлеровым является граф …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дифференциальная геометрия кривых
Траектория
движущейся точки задается уравнением
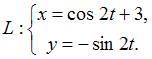 Тогда
значение касательного ускорения в
момент
Тогда
значение касательного ускорения в
момент
![]() равно
…
равно
…
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение:
Касательное
ускорение на параметрически заданной
кривой вычисляется как
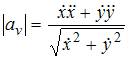 .
Вычислим
производные первого и второго
порядка.
.
Вычислим
производные первого и второго
порядка.
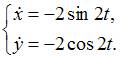
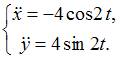 Найдем
Найдем
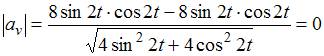 ,
при любых значениях
,
при любых значениях
![]() .
.
ЗАДАНИЕ N 10 Тема: Дифференциальная геометрия поверхностей
Точка
с координатами
![]() на
поверхности
на
поверхности
![]() является
…
является
…
|
|
|
гиперболической точкой |
|
|
|
параболической точкой |
|
|
|
эллиптической точкой |
|
|
|
точкой уплощения |
Решение:
Тип
точки на поверхности определяется по
виду соприкасающегося параболоида в
этой точке к поверхности.
Построим
соприкасающийся параболоид:
![]() .
Вычислим
частные производные второго порядка:
.
Вычислим
частные производные второго порядка:
![]() ;
;
 ;
;
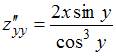 .
В
точке
;
.
В
точке
;
![]() ;
;
![]() .
Тогда
соприкасающийся параболоид
.
Тогда
соприкасающийся параболоид
![]() является
гиперболическим параболоидом, а сама
точка
относится
к гиперболическому типу.
является
гиперболическим параболоидом, а сама
точка
относится
к гиперболическому типу.
Задание n 11 Тема: Асимптоты кривой
Асимптоты
кривой
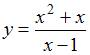 имеют
вид …
имеют
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Кривая
описывается соотношением
 ,
то есть функция представлена в явном
виде.
В точке
функция
имеет разрыв, поэтому уравнение
вертикальной асимптоты имеет вид:
.
Наклонные
или горизонтальные асимптоты определяются
уравнением
,
то есть функция представлена в явном
виде.
В точке
функция
имеет разрыв, поэтому уравнение
вертикальной асимптоты имеет вид:
.
Наклонные
или горизонтальные асимптоты определяются
уравнением
![]() (для
горизонтальных асимптот
(для
горизонтальных асимптот
![]() ).
1.
Находим асимптоту
).
1.
Находим асимптоту
![]() при
при
![]() (правую
асимптоту):
(правую
асимптоту):
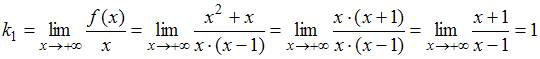 ,
,
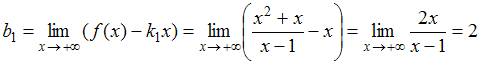 .
Следовательно,
уравнение правой асимптоты имеет вид:
.
2.
Аналогично находим асимптоту
.
Следовательно,
уравнение правой асимптоты имеет вид:
.
2.
Аналогично находим асимптоту
![]() при
при
![]() (левую
асимптоту):
(левую
асимптоту):
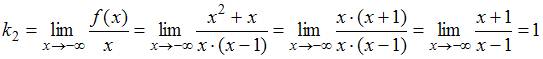 ,
,
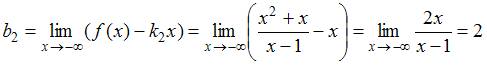 .
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптоты и имеет
вид:
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
.
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптоты и имеет
вид:
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
Задание n 12 Тема: Основные понятия топологии
Внешностью
множества
![]() в
топологическом пространстве
в
топологическом пространстве
![]() с
топологией
с
топологией
![]() является
…
является
…
|
|
|
пустое множество |
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Внешность M – это совокупность всех внутренних точек дополнения к множеству M, то есть входящих в дополнение к M с какой-либо своей окрестностью (открытым множеством). Дополнением является множество – закрытое множество, которое не содержит в себе ни одного открытого множества из данной топологии. Таким образом, внешностью множества в данном случае будет пустое множество.
ЗАДАНИЕ N 13 Тема: Непрерывность функции, точки разрыва
Для
функции
![]() точка
точка
![]() является
точкой …
является
точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
ЗАДАНИЕ N 14 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное
значение функции
![]() при
при
![]() ,
вычисленное с использованием дифференциала
первого порядка, равно …
,
вычисленное с использованием дифференциала
первого порядка, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 15 Тема: Дифференциальное исчисление ФНП
Частная
производная
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 16 Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
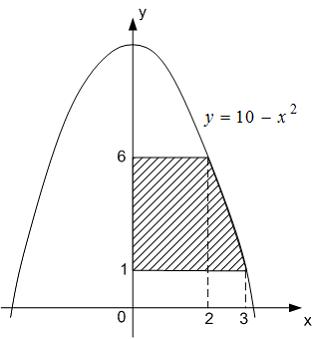 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 17 Тема: Поле направлений и изоклины
Поле
направлений дифференциального уравнения
![]() определяется
неравенством …
определяется
неравенством …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как поле направлений дифференциального
уравнения
![]() задано
в области определения функции двух
переменных
задано
в области определения функции двух
переменных
![]() ,
то для нахождения области задания поля
направлений следует решить неравенство
,
то для нахождения области задания поля
направлений следует решить неравенство
![]() .
Тогда
.
.
Тогда
.
ЗАДАНИЕ N 18 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее
решение системы дифференциальных
уравнений
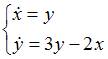 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 Тема: Задача Коши для дифференциального уравнения первого порядка
Функция
![]() является
общим решением дифференциального
уравнения 1-го порядка. Тогда для
начального условия
является
общим решением дифференциального
уравнения 1-го порядка. Тогда для
начального условия
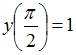 частное
решение этого уравнения имеет вид …
частное
решение этого уравнения имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 20 Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное
уравнение
![]() будет
уравнением с разделяющимися переменными
при значении
будет
уравнением с разделяющимися переменными
при значении
![]() ,
равном …
,
равном …
|
|
|
2 |
|
|
|
0 |
|
|
|
4 |
|
|
|
1 |
Решение:
Данное
уравнение можно представить в виде
![]() .
Это уравнение будет уравнением с
разделяющимися переменными при
.
Это уравнение будет уравнением с
разделяющимися переменными при
![]() ,
то есть при
,
то есть при
![]() .
Откуда
.
Откуда
![]() .
.
ЗАДАНИЕ N 21 Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Решение:
Для
вычисления события
(сумма
выпавших очков будет не меньше девяти)
воспользуемся формулой
![]() ,
где
,
где
![]() –
общее число возможных элементарных
исходов испытания, а m
– число элементарных исходов,
благоприятствующих появлению события
A.
В нашем случае возможны
–
общее число возможных элементарных
исходов испытания, а m
– число элементарных исходов,
благоприятствующих появлению события
A.
В нашем случае возможны
![]() элементарных
исходов испытания, из которых
благоприятствующими являются исходы
вида
элементарных
исходов испытания, из которых
благоприятствующими являются исходы
вида
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
то есть
,
то есть
![]() .
Следовательно,
.
Следовательно,
![]() .
.
ЗАДАНИЕ N 22 Тема: Числовые характеристики случайных величин
Непрерывная
случайная величина
задана
плотностью распределения вероятностей:
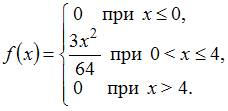 Тогда
ее математическое ожидание равно …
Тогда
ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 23 Тема: Законы распределения вероятностей дискретных случайных величин
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
|
|
|
0,0081 |
|
|
|
0,081 |
|
|
|
0,06 |
|
|
|
0,0729 |
ЗАДАНИЕ N 24 Тема: Полная вероятность. Формулы Байеса
Имеются четыре урны, содержащие по 3 белых и 7 черных шаров, и шесть урн, содержащих по 8 белых и 2 черных шара. Из наудачу взятой урны вытаскивается один шар, который оказался белым. Тогда вероятность того, что этот шар был вынут из первой серии урн, равна …
|
|
|
0,20 |
|
|
|
0,80 |
|
|
|
0,72 |
|
|
|
0,40 |
Решение:
Предварительно
вычислим вероятность события A
(вынутый наудачу шар – белый) по формуле
полной вероятности:
![]() .
Здесь
.
Здесь
![]() –
вероятность того, что шар извлечен из
первой серии урн;
–
вероятность того, что шар извлечен из
первой серии урн;
![]() –
вероятность того, что шар извлечен из
второй серии урн;
–
вероятность того, что шар извлечен из
второй серии урн;
![]() –
условная вероятность того, что вынутый
шар белый, если из он извлечен из первой
серии урн;
–
условная вероятность того, что вынутый
шар белый, если из он извлечен из первой
серии урн;
![]() –
условная вероятность того, что вынутый
шар белый, если из он извлечен из второй
серии урн.
Тогда
–
условная вероятность того, что вынутый
шар белый, если из он извлечен из второй
серии урн.
Тогда
![]() .
Теперь
вычислим условную вероятность того,
что этот шар был извлечен из первой
серии урн, по формуле Байеса:
.
Теперь
вычислим условную вероятность того,
что этот шар был извлечен из первой
серии урн, по формуле Байеса:
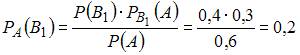 .
.
ЗАДАНИЕ N 25 Тема: Мера плоского множества
Мера
плоского множества
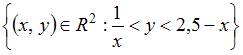 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 26 Тема: Метрические пространства
Расстояние
между точками
![]() и
и
![]() в
метрике
в
метрике
![]() ,
где
,
где
![]() и
и
![]() ,
равно …
,
равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
Решение:
![]() .
.
ЗАДАНИЕ N 27 Тема: Элементы теории множеств
Даны
три множества:
![]() ,
,
![]() и
и
![]() .
Тогда число элементов множества
.
Тогда число элементов множества
![]() равно
…
равно
…
|
1 | |
Решение:
Определим
множество
![]() и
выполним операцию пересечения
и
выполним операцию пересечения
![]() .
В результате получится множество
.
В результате получится множество
![]() ,
состоящее из одного элемента.
,
состоящее из одного элемента.
ЗАДАНИЕ N 28 Тема: Отображение множеств
Пусть
задано отображение
![]() .
Тогда
.
Тогда
![]() представляет
собой …
представляет
собой …
|
|
|
единичную окружность |
|
|
|
отрезок
|
|
|
|
квадрат |
|
|
|
гиперболу |
ЗАДАНИЕ N 29 Тема: Линейные отображения
Пусть
![]() –
базис пространства
–
базис пространства
![]() .
Операторы
.
Операторы
![]() и
и
![]() этого
пространства заданы матрицами
этого
пространства заданы матрицами
 ;
;
 .
Тогда матрица оператора
.
Тогда матрица оператора
![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
![]()
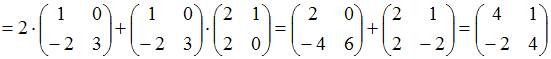 .
.
ЗАДАНИЕ N 30 Тема: Основные алгебраические структуры
Обратным
элементом для матрицы
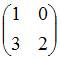 относительно
операции сложения матриц является …
относительно
операции сложения матриц является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 31 Тема: Дробно-рациональные функции
Множество
всех дробно-рациональных функций
образует поле
![]() относительно
обычных операций сложения и умножения
таких функций.
Пусть
относительно
обычных операций сложения и умножения
таких функций.
Пусть
![]() и
и
![]() ,
причем
,
причем
 и
и
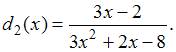 Тогда
числитель суммы
Тогда
числитель суммы
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Разложим
на линейные множители знаменатели
дробно-рациональных функций
![]() и
и
![]() :
:
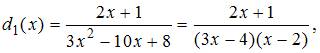
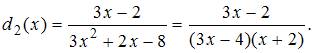 Тогда
Тогда
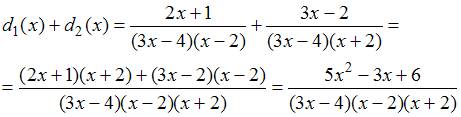 То
есть, числитель суммы
равен
.
То
есть, числитель суммы
равен
.
ЗАДАНИЕ N 32 Тема: Группы и подгруппы
На множестве целых чисел группу образует операция * определенная как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 33 Тема: Кривые второго порядка
Уравнение
директрисы параболы, проходящей через
точки
![]() ,
,
![]() и
симметричной относительно оси
и
симметричной относительно оси
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Каноническое
уравнение параболы, проходящей через
начало координат и симметричной
относительно оси
имеет
вид:
![]() ,
а уравнение директрисы:
,
а уравнение директрисы:
![]() .
Параметр
.
Параметр
![]() находится
из условия, что точка
принадлежит
параболе, то есть
находится
из условия, что точка
принадлежит
параболе, то есть
![]() ,
,
![]() .
Тогда уравнение директрисы параболы
примет вид:
.
.
Тогда уравнение директрисы параболы
примет вид:
.
ЗАДАНИЕ N 34 Тема: Прямоугольные координаты на плоскости
Точки
![]() и
и
![]() лежат
на одной прямой, параллельной оси
ординат. Расстояние между точками
и
лежат
на одной прямой, параллельной оси
ординат. Расстояние между точками
и
![]() равно
6. Тогда положительные координаты точки
равны
…
равно
6. Тогда положительные координаты точки
равны
…
|
|
|
|
|
|
|
|
|
|
|
,
|
|
|
|
, |
Решение:
Точки,
лежащие на одной прямой, параллельной
оси OY, имеют одинаковые абсциссы,
следовательно,
и
![]() .
Расстояние между двумя точками
.
Расстояние между двумя точками
![]() и
и
![]() находится
по формуле
находится
по формуле
![]() .
Тогда расстояние между точками
и
можно
найти как
.
Тогда расстояние между точками
и
можно
найти как
![]() .
Из
условия
.
Из
условия
![]() ,
получаем
,
получаем
![]() ,
или
,
или
![]() .
Следовательно,
.
Следовательно,
![]() ;
;
![]() .
Тогда положительные координаты точки
равны:
,
.
.
Тогда положительные координаты точки
равны:
,
.
ЗАДАНИЕ N 35 Тема: Плоскость в пространстве
Уравнение
плоскости, проходящей через точку
![]() параллельно
векторам
параллельно
векторам
![]() и
и
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости, проходящей через точку
![]() с
нормальным вектором
с
нормальным вектором
![]() ,
имеет вид:
,
имеет вид:
![]() .
В качестве нормального вектора плоскости
возьмем векторное произведение векторов
.
В качестве нормального вектора плоскости
возьмем векторное произведение векторов
![]() и
и
![]() .
Тогда
.
Тогда
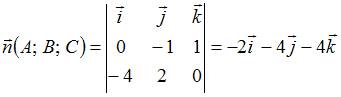 ,
или
,
или
![]() .
Подставляя в уравнение плоскости
координаты точки
и
вектора
.
Подставляя в уравнение плоскости
координаты точки
и
вектора
![]() ,
получим:
,
получим:
![]() или
.
или
.
ЗАДАНИЕ N 36 Тема: Прямая линия в пространстве
Острый
угол между прямыми
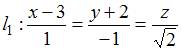 и
и
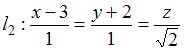 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Угол
между прямыми
![]() и
и
![]() определяется
как угол между их направляющими векторами:
определяется
как угол между их направляющими векторами:
![]() и
и
![]() ,
который можно вычислить по формуле:
,
который можно вычислить по формуле:
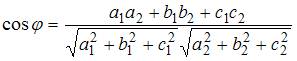 .
Тогда
.
Тогда
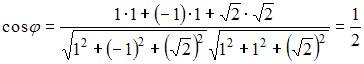 ,
то есть
,
то есть
![]() .
.
ЗАДАНИЕ N 37 Тема: Особые точки функции комплексного переменного
Число
особых точек функции
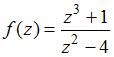 равно
…
равно
…
|
|
|
3 |
|
|
|
5 |
|
|
|
2 |
|
|
|
1 |
Решение:
Для
функции
точки
![]() –
полюсы первого порядка,
–
полюсы первого порядка,
![]() –
полюс первого порядка.
Следовательно,
число особых точек равно трем.
–
полюс первого порядка.
Следовательно,
число особых точек равно трем.
ЗАДАНИЕ N 38 Тема: Дифференцирование функции комплексного переменного
Если
![]() и
и
![]() ,
то мнимая часть производной этой функции
,
то мнимая часть производной этой функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 39 Тема: Области на комплексной плоскости
Все
точки
![]() комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
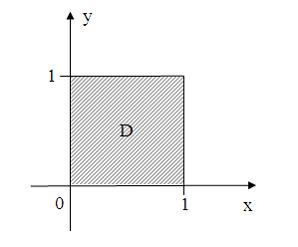 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 40 Тема: Операции над комплексными числами
Дано
комплексное число
![]() .
Тогда
.
Тогда
![]() равно
…
равно
…
|
|
|
16 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение:
Если
комплексное число
![]() в
тригонометрической форме имеет вид
в
тригонометрической форме имеет вид
![]() ,
то по формуле Муавра
,
то по формуле Муавра
![]() ,
где
,
где
![]() –
натуральное число.
Запишем число
в
тригонометрической форме:
1) находим
модуль числа
–
натуральное число.
Запишем число
в
тригонометрической форме:
1) находим
модуль числа
![]() ;
2)
составляем систему уравнений для
нахождения аргумента
;
2)
составляем систему уравнений для
нахождения аргумента
![]() и
главного значения аргумента:
и
главного значения аргумента:
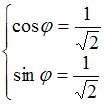 3)
находим главное значение аргумента
комплексного числа
,
которое равно
3)
находим главное значение аргумента
комплексного числа
,
которое равно
![]() ;
4)
тогда
;
4)
тогда
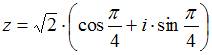 .
Следовательно,
.
Следовательно,
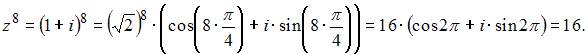
Математика i-exam вариант 2
ЗАДАНИЕ N 1 Тема: Плоскость в пространстве
Угол
между плоскостями
![]() и
и
![]() равен
…
равен
…
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 2 Тема: Кривые второго порядка
Радиус
окружности
![]() равен
…
равен
…
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
Решение:
Окружность
радиуса
![]() с
центром в точке
с
центром в точке
![]() задается
на плоскости уравнением вида
задается
на плоскости уравнением вида
![]() .
Выделим в уравнении
полные
квадраты:
.
Выделим в уравнении
полные
квадраты:
![]() ,
или
,
или
![]() .
Тогда
радиус окружности равен 2.
.
Тогда
радиус окружности равен 2.
ЗАДАНИЕ N 3 Тема: Прямая линия в пространстве
Каноническое
уравнение прямой
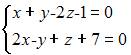 может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 4 Тема: Прямоугольные координаты на плоскости
Даны
точки
![]() и
и
![]() .
Тогда координаты точки
.
Тогда координаты точки
![]() ,
симметричной точке
относительно
точки
,
равны …
,
симметричной точке
относительно
точки
,
равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 5 Тема: Дифференциальные уравнения с разделяющимися переменными
Общее
решение дифференциального уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 6 Тема: Поле направлений и изоклины
Дано
дифференциальное уравнение
![]() .
Тогда отрезок соответствующего ему
поля направлений в точке
.
Тогда отрезок соответствующего ему
поля направлений в точке
![]() образует
с осью
угол,
равный …
образует
с осью
угол,
равный …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 7 Тема: Задача Коши для дифференциального уравнения первого порядка
Частное
решение дифференциального уравнения
![]() ,
удовлетворяющее условию
,
удовлетворяющее условию
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 8 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее
решение системы дифференциальных
уравнений
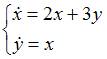 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дифференциальное исчисление ФНП
Частная производная функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 10 Тема: Непрерывность функции, точки разрыва
Количество
точек разрыва функции
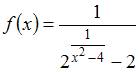 равно
…
равно
…
|
|
|
4 |
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
Решение:
Точку
![]() называют
точкой разрыва функции
называют
точкой разрыва функции
![]() ,
если она не является непрерывной в этой
точке. В частности, точками разрыва
данной функции являются точки, в которых
знаменатели равны нулю. То есть
,
если она не является непрерывной в этой
точке. В частности, точками разрыва
данной функции являются точки, в которых
знаменатели равны нулю. То есть
![]() ,
и
,
и
![]() .
Тогда
.
Тогда
![]() ,
,
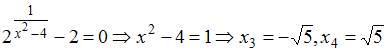 .
Следовательно,
получили четыре точки разрыва функции.
.
Следовательно,
получили четыре точки разрыва функции.
ЗАДАНИЕ N 11 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Предел
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 12 Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 13 Тема: Асимптоты кривой
Асимптоты
графика кривой
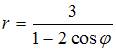 ,
заданной в полярных координатах, имеют
вид …
,
заданной в полярных координатах, имеют
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 14 Тема: Дифференциальная геометрия поверхностей
Вектор
нормали
![]() в
точке
в
точке
![]() к
поверхности тора
к
поверхности тора
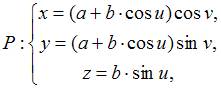 имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вычислим
частные производные в точке
:
![]() ;
;
![]() ;
Тогда
вектор нормали в точке
;
Тогда
вектор нормали в точке
![]() будет
равен:
будет
равен:
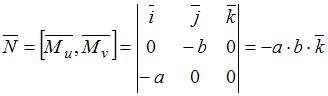 .
.
ЗАДАНИЕ N 15 Тема: Дифференциальная геометрия кривых
Уравнение
нормали к кривой
![]() в
точке
в
точке
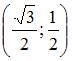 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 16 Тема: Основные понятия топологии
Внутренностью множества в топологическом пространстве с топологией является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пустое множество |
Решение: Внутренность – это совокупность всех внутренних точек множества, то есть точек из , входящих в с какой-либо своей окрестностью (открытым множеством). Таким образом, внутренностью множества в данном случае является множество .
ЗАДАНИЕ N 17 Тема: Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
![]() на
на
![]() имеет
вид
имеет
вид
![]() .
Тогда выборочный коэффициент корреляции
может быть равен …
.
Тогда выборочный коэффициент корреляции
может быть равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 18 Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 Тема: Проверка статистических гипотез
Левосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 20 Тема: Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
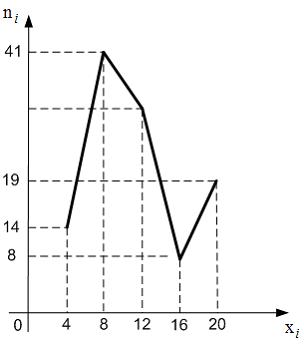 Тогда
число вариант
Тогда
число вариант
![]() в
выборке равно …
в
выборке равно …
|
|
|
32 |
|
|
|
82 |
|
|
|
8 |
|
|
|
31 |
ЗАДАНИЕ N 21 Тема: Операции над высказываниями
Таблица
истинности для формулы
![]() представляет
собой …
представляет
собой …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 22 Тема: Декартово произведение множеств
Декартово
произведение множеств
![]() и
и
![]() представляет
собой …
представляет
собой …
|
|
|
окружность , лежащую в плоскости |
|
|
|
цилиндрическую поверхность |
|
|
|
сферу
|
|
|
|
эллиптический
параболоид
|
ЗАДАНИЕ N 23 Тема: Элементы комбинаторики
Вокруг костра сидят 12 разбойников. Каждый из них смертельно ненавидит двух ближайших соседей. С целью спрятать награбленное необходимо выделить 5 разбойников. Сколькими способами атаман может назначить пятерых так, чтобы между ними не было распрей?
|
12 |
ЗАДАНИЕ N 24 Тема: Неориентированные графы
Для
графа, изображенного на
рисунке,
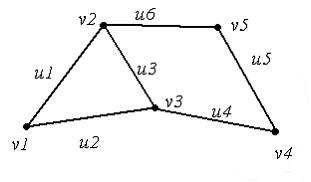 последовательность
последовательность
![]() является
…
является
…
|
|
|
маршрутом |
|
|
|
цепью |
|
|
|
циклом |
|
|
|
деревом |
Решение:
Маршрутом
называют последовательность вершин и
ребер некоторого графа. Маршрут, не
содержащий повторяющихся ребер, называют
цепью. Замкнутая цепь называется циклом.
Деревом называют простой граф, не
содержащий в себе циклов.
Последовательность
не
замкнута, содержит в себе повторяющееся
ребро
![]() ,
включает в себя цикл
,
включает в себя цикл
![]() .
Поэтому она не является, ни «цепью», ни
«циклом», ни «деревом»; а представляет
собой просто «маршрут».
.
Поэтому она не является, ни «цепью», ни
«циклом», ни «деревом»; а представляет
собой просто «маршрут».
ЗАДАНИЕ N 25 Тема: Полная вероятность. Формулы Байеса
В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 26 Тема: Определение вероятности
Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 27 Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная
случайная величина
задана
функцией распределения вероятностей
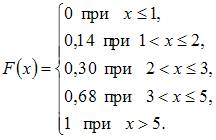 Тогда
вероятность
Тогда
вероятность
![]() равна
…
равна
…
|
|
|
0,54 |
|
|
|
0,38 |
|
|
|
0,70 |
|
|
|
0,86 |
Решение:
Так
как по определению
![]() ,
то случайную величину
можно
задать законом распределения вероятностей
вида
,
то случайную величину
можно
задать законом распределения вероятностей
вида
 Следовательно,
Следовательно,
![]() .
.
ЗАДАНИЕ N 28 Тема: Числовые характеристики случайных величин
Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 29 Тема: Особые точки функции комплексного переменного
Для
функции
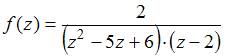 точка
точка
![]() является
…
является
…
|
|
|
полюсом второго порядка |
|
|
|
полюсом третьего порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
ЗАДАНИЕ N 30 Тема: Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
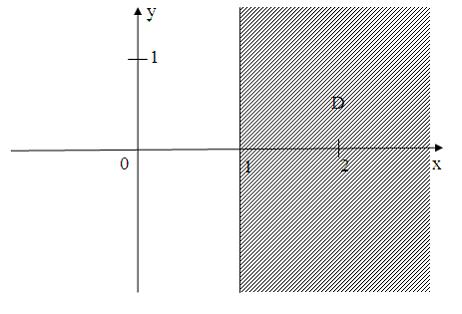 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 31 Тема: Операции над комплексными числами
Если
![]() и
и
![]() –
корни квадратного уравнения
–
корни квадратного уравнения
![]() ,
то
,
то
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Решение
квадратного уравнения
![]() находится
по формуле
находится
по формуле
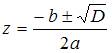
![]() ,
где под
,
где под
![]() понимаются
все значения корня из комплексного
числа
.
В нашем случае
понимаются
все значения корня из комплексного
числа
.
В нашем случае
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
Решение
можно найти и по теореме Виета. Так как
.
Решение
можно найти и по теореме Виета. Так как
![]() ,
то в нашем случае получим, что
,
то в нашем случае получим, что
![]() .
.
ЗАДАНИЕ N 32 Тема: Дифференцирование функции комплексного переменного
Если и , то мнимая часть производной этой функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Производная
функции
равна
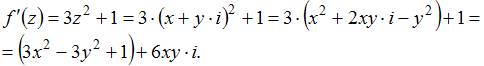 Тогда
Тогда
![]() .
.
ЗАДАНИЕ N 33 Тема: Мера плоского множества
Мера плоского множества равна …
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 34 Тема: Элементы теории множеств
Даны
два множества:
![]() и
и
![]() .
Тогда количество целых значений
.
Тогда количество целых значений
![]() ,
принадлежащих пересечению множеств
и
,
равно …
,
принадлежащих пересечению множеств
и
,
равно …
|
4 |
ЗАДАНИЕ N 35 Тема: Отображение множеств
Прообразом
множества
![]() при
отображении
при
отображении
![]() является
…
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 36 Тема: Метрические пространства
Расстояние между точками и в метрике , где и , равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
Решение: .
ЗАДАНИЕ N 37 Тема: Основные алгебраические структуры
В кольце квадратных матриц второго порядка единичный элемент …
|
|
|
– это
матрица
|
|
|
|
– это
матрица
|
|
|
|
– это
матрица
|
|
|
|
не существует |
ЗАДАНИЕ N 38 Тема: Группы и подгруппы
Подгруппой группы целых чисел с введенной операцией сложения является множество …
|
|
|
четных целых чисел |
|
|
|
нечетных целых чисел |
|
|
|
натуральных чисел |
|
|
|
натуральных чисел с нулем |
ЗАДАНИЕ N 39 Тема: Дробно-рациональные функции
Даны
два полинома:
![]() и
и
![]() Тогда
целая часть от деления полинома
Тогда
целая часть от деления полинома
![]() на
полином
на
полином
![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выполним
деление заданных полиномов
«уголком»:
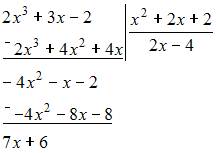 Тогда:
Тогда:
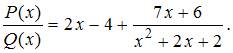 То
есть, целая часть от деления полинома
на
полином
равна
То
есть, целая часть от деления полинома
на
полином
равна
![]()
ЗАДАНИЕ N 40 Тема: Линейные отображения
Линейный
оператор
отображает
базис
![]() в
векторы:
в
векторы:
![]() ;
;
![]() ;
;
![]() .
Тогда матрица оператора
в
этом базисе имеет вид …
.
Тогда матрица оператора
в
этом базисе имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
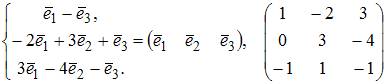 .
.
Математика i-exam вариант 3
ЗАДАНИЕ N 1 Тема: Приложения определенного интеграла
Объем
тела, полученного вращением вокруг оси
криволинейной
трапеции, ограниченной параболой
![]() и
осью
,
равен …
и
осью
,
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 2 Тема: Непрерывность функции, точки разрыва
Количество точек разрыва функции равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
Решение: Точку называют точкой разрыва функции , если она не является непрерывной в этой точке. В частности, точками разрыва данной функции являются точки, в которых знаменатели равны нулю. То есть , и . Тогда , . Следовательно, получили четыре точки разрыва функции.
ЗАДАНИЕ N 3 Тема: Дифференциальное исчисление ФНП
Смешанная
частная производная второго порядка
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 4 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное значение функции при , вычисленное с использованием дифференциала первого порядка, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 5 Тема: Операции над высказываниями
Нулевой
набор у формулы
![]() получается
при следующих значениях переменных …
получается
при следующих значениях переменных …
|
|
|
|
|
|
|
|
|
|
|
,
|
|
|
|
, |
ЗАДАНИЕ N 6 Тема: Неориентированные графы
Для
графа G, изображенного на рисунке,
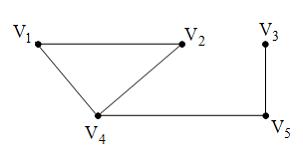 матрица
смежности имеет вид …
матрица
смежности имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 7 Тема: Элементы комбинаторики
В урне находятся 5 белых, 7 красных, 6 голубых шаров. Сколько существует способов извлечь 9 шаров так, чтобы среди них оказалось 2 белых, 3 красных и 4 голубых шара?
|
5250 |
ЗАДАНИЕ N 8 Тема: Декартово произведение множеств
Пусть
даны два множества:
![]() ,
,
![]() .
Тогда
геометрическая интерпретация множества
имеет
вид …
.
Тогда
геометрическая интерпретация множества
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дробно-рациональные функции
Даны два полинома: и Тогда целая часть от деления полинома на полином равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Выполним деление заданных полиномов «уголком»: Тогда: То есть, целая часть от деления полинома на полином равна
ЗАДАНИЕ N 10 Тема: Линейные отображения
Прообразом
вектора
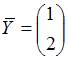 при
линейном преобразовании, заданном
матрицей
при
линейном преобразовании, заданном
матрицей
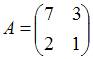 ,
является вектор …
,
является вектор …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 11 Тема: Основные алгебраические структуры
Для
кольца
![]() множество
множество
![]() ,
рассматриваемое с одной алгебраической
операцией сложения, представляет собой
…
,
рассматриваемое с одной алгебраической
операцией сложения, представляет собой
…
|
|
|
абелеву группу |
|
|
|
поле |
|
|
|
целостное кольцо |
|
|
|
область целостности |
ЗАДАНИЕ N 12 Тема: Группы и подгруппы
Подгруппой группы невырожденных матриц по умножению является подмножество матриц с …
|
|
|
единичным определителем |
|
|
|
определителем, равным 2 |
|
|
|
определителем, равным – 1 |
|
|
|
определителями, равными 2 и 0,5 |
ЗАДАНИЕ N 13 Тема: Определение вероятности
Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 14 Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
значения a
и b
могут быть равны …
Тогда
значения a
и b
могут быть равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 15 Тема: Числовые характеристики случайных величин
Дискретная
случайная величина X
задана законом распределения
вероятностей:
 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
7,56 |
|
|
|
3,2 |
|
|
|
3,36 |
|
|
|
6,0 |
ЗАДАНИЕ N 16 Тема: Полная вероятность. Формулы Байеса
В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 17 Тема: Дифференциальная геометрия поверхностей
Вектор
нормали
к
прямому геликоиду
![]() в
точке
в
точке
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Найдем
частные производные:
![]() ;
;
![]() .
Тогда
.
Тогда
![]() и
и
![]() ,
и вектор нормали будет равен:
,
и вектор нормали будет равен:
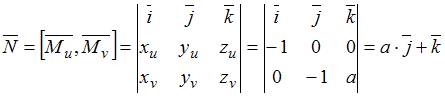 ;
или
;
или
![]() .
.
ЗАДАНИЕ N 18 Тема: Асимптоты кривой
Асимптоты
кривой
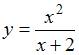 имеют
вид …
имеют
вид …
|
|
|
и |
|
|
|
|
|
|
|
и
|
|
|
|
и |
ЗАДАНИЕ N 19 Тема: Дифференциальная геометрия кривых
Длина
дуги кривой
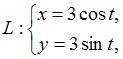 при
при
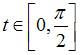 ,
равна …
,
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,14 |
Решение:
Длина
дуги кривой вычисляется по формуле:
 ,
где
,
где
![]() -
дифференциал дуги. Вычислив
-
дифференциал дуги. Вычислив
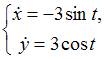 ,
получаем
,
получаем
![]() .
Тогда
.
Тогда
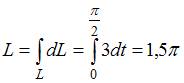 .
.
ЗАДАНИЕ N 20 Тема: Основные понятия топологии
Гомеоморфной к тору является …
|
|
|
«кружка с ручкой» |
|
|
|
сфера |
|
|
|
«крендель» |
|
|
|
куб |
ЗАДАНИЕ N 21 Тема: Интервальные оценки параметров распределения
Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна 3,5. Тогда его интервальная оценка может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Интервальной
оценкой среднего квадратического
отклонения
![]() нормально
распределенного количественного
признака служит доверительный
интервал
нормально
распределенного количественного
признака служит доверительный
интервал
![]() при
при
![]() или
или
![]() при
при
![]() ,
где q
находят по соответствующей таблице
приложений.
Этому определению
удовлетворяет интервал
.
,
где q
находят по соответствующей таблице
приложений.
Этому определению
удовлетворяет интервал
.
ЗАДАНИЕ N 22 Тема: Проверка статистических гипотез
Правосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 23 Тема: Статистическое распределение выборки
Статистическое
распределение выборки имеет вид
 Тогда
значение относительной частоты
Тогда
значение относительной частоты
![]() равно
…
равно
…
|
|
|
0,25 |
|
|
|
0,05 |
|
|
|
0,26 |
|
|
|
0,75 |
ЗАДАНИЕ N 24 Тема: Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
на
имеет
вид
![]() .
Тогда выборочный коэффициент регрессии
равен …
.
Тогда выборочный коэффициент регрессии
равен …
|
|
|
– 1,5 |
|
|
|
1,5 |
|
|
|
4 |
|
|
|
|
Решение:
Если
выборочное уравнение парной регрессии
имеет вид
![]() ,
то выборочный коэффициент регрессии
равен
,
то выборочный коэффициент регрессии
равен
![]() .
То есть
.
То есть
![]() .
.
ЗАДАНИЕ N 25 Тема: Операции над комплексными числами
Дано комплексное число . Тогда равно …
|
|
|
16 |
|
|
|
|
|
|
|
2 |
|
|
|
|
ЗАДАНИЕ N 26 Тема: Особые точки функции комплексного переменного
Число особых точек функции равно …
|
|
|
3 |
|
|
|
5 |
|
|
|
2 |
|
|
|
1 |
Решение: Для функции точки – полюсы первого порядка, – полюс первого порядка. Следовательно, число особых точек равно трем.
ЗАДАНИЕ N 27 Тема: Дифференцирование функции комплексного переменного
Значение
производной функции
![]() в
точке
в
точке
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Производная
функции
имеет
вид
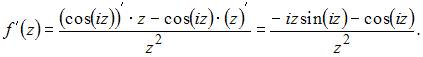 Тогда
Тогда
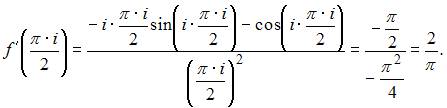
ЗАДАНИЕ N 28 Тема: Области на комплексной плоскости
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке, удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Математика i-exam вариант 4
ЗАДАНИЕ N 1 Тема: Области на комплексной плоскости
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке: удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 2 Тема: Операции над комплексными числами
Произведение
комплексных чисел
![]() и
и
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 3 Тема: Дифференцирование функции комплексного переменного
Если
![]() ,
то
,
то
![]() равно
…
равно
…
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
Решение:
Производная
функции
равна
![]() .
Тогда
.
Тогда
![]() .
.
ЗАДАНИЕ N 4 Тема: Особые точки функции комплексного переменного
Для
функции
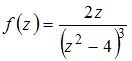 точка
является
…
точка
является
…
|
|
|
полюсом третьего порядка |
|
|
|
полюсом второго порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
Решение:
Порядок
полюса функции вида
 равен
порядку нуля
равен
порядку нуля
![]() .
Имеем
.
Имеем
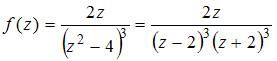 ,
поэтому
точка
будет
полюсом третьего порядка.
,
поэтому
точка
будет
полюсом третьего порядка.
ЗАДАНИЕ N 5 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Решим
систему дифференциальных уравнений
методом исключения.
Из второго
уравнения находим производную
![]() и
после подстановки выражений для
и
и
после подстановки выражений для
и
![]() в
первое уравнение системы получим
линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами
в
первое уравнение системы получим
линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами
![]() .
Характеристическое
уравнение
.
Характеристическое
уравнение
![]() имеет
два действительных корня:
имеет
два действительных корня:
![]() .
Таким
корням соответствует общее решение
однородного дифференциального уравнения
.
Таким
корням соответствует общее решение
однородного дифференциального уравнения
![]() .
Дифференцируя полученное решение,
находим
.
Дифференцируя полученное решение,
находим
![]() .
Тогда
общее решение системы уравнений имеет
вид
.
.
Тогда
общее решение системы уравнений имеет
вид
.
ЗАДАНИЕ N 6 Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное
уравнение
![]() будет
уравнением с разделяющимися переменными
при значении
,
равном …
будет
уравнением с разделяющимися переменными
при значении
,
равном …
|
|
|
2 |
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Решение:
Данное
уравнение можно представить в виде:
![]() .
Это
уравнение будет уравнением с разделяющимися
переменными при
.
Это
уравнение будет уравнением с разделяющимися
переменными при
![]() ,
то есть при
.
Откуда
.
,
то есть при
.
Откуда
.
ЗАДАНИЕ N 7 Тема: Поле направлений и изоклины
Дано
дифференциальное уравнение
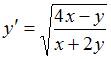 .
Тогда отрезок соответствующего ему
поля направлений в точке
.
Тогда отрезок соответствующего ему
поля направлений в точке
![]() образует
с осью
угол
при
образует
с осью
угол
при
![]() равном…
равном…
|
|
|
2 |
|
|
|
14 |
|
|
|
|
|
|
|
|
Решение:
Так
как дифференциальное уравнение имеет
вид
![]() ,
то угол
определяется
из равенства
,
то угол
определяется
из равенства
![]() ,
где
,
где
![]() –
координаты точки
.
В
рассматриваемом случае
–
координаты точки
.
В
рассматриваемом случае
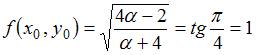 ,
то есть
,
то есть
![]() .
Следовательно,
.
.
Следовательно,
.
ЗАДАНИЕ N 8 Тема: Задача Коши для дифференциального уравнения первого порядка
Решение
задачи Коши
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дробно-рациональные функции
Разложение
дробно-рациональной функции
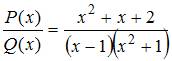 на
простые дроби над полем вещественных
чисел имеет вид …
на
простые дроби над полем вещественных
чисел имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 10 Тема: Основные алгебраические структуры
Алгеброй является …
|
|
|
множество рациональных чисел и операция умножения |
|
|
|
пустое множество и операция пересечения |
|
|
|
множество натуральных чисел и операция векторного произведения |
|
|
|
множество целых чисел и отношение порядка |
Решение:
Алгеброй
называется пара
![]() ,
состоящая из непустого множества
и
множества
,
состоящая из непустого множества
и
множества
![]() ,
заданных на нем операций.
Тогда пустое
множество и операция пересечения не
являются алгеброй, так как множество
не
может быть пустым.
Множество натуральных
чисел и операция векторного произведения
не являются алгеброй, так как операция
векторного произведения задается на
множестве векторов, а не на множестве
натуральных чисел.
Множество целых
чисел и отношение порядка не являются
алгеброй, так как не задана ни одна
операция.
Множество рациональных
чисел и операция умножения являются
алгеброй.
,
заданных на нем операций.
Тогда пустое
множество и операция пересечения не
являются алгеброй, так как множество
не
может быть пустым.
Множество натуральных
чисел и операция векторного произведения
не являются алгеброй, так как операция
векторного произведения задается на
множестве векторов, а не на множестве
натуральных чисел.
Множество целых
чисел и отношение порядка не являются
алгеброй, так как не задана ни одна
операция.
Множество рациональных
чисел и операция умножения являются
алгеброй.