2. Дать сравнительную оценку силы связи факторов с результатами с помощью коэффициента эластичности и стандартизированных коэффициентов регрессии.

Коэффициент эластичности
	0,046099
	-0,21937
	0,163893
	-0,2368

Это означает , что при увеличении значения х1 на 1% увеличение у составит 0,046%, второго – уменьшение у составит 0,219, увеличение третьего на 1% вызовет увеличение результирующего показателя на 0,164%, а увеличение четвертого фактора вызовет уменьшение на 0,237%.

средние	53,47059	4,31764706	2,582353	2,529412	90,58824
дисперсия	22,76471	3,18404412	0,190294	0,170956	435,1324
СКО	4,771237	1,784389	0,436227	0,413468	20,85983
стандартизированный коэффициент регрессии		14,912748	3,645699	3,455494	174,3327

Увеличение первого фактора на 1,784 вызовет увеличение результирующего показателя на 14,913, изменение второго на 0,436 приведет к увеличению у на 3,646, увеличение третьего на 0,413 приведет к увеличению у на 3,455, четвертого на 20,86 вызовет увеличение у на 174,332.

3. Оценить значимость полученного уравнения регрессии.

F-статистика	Уровень значимости	F(gama,1,n-2)	Решение
25,68864	0,05	0,004066	Значима

При коэффициенте детерминации равном 0,77 и F – теста регрессия признается значимой.

Задание 26

Постройте авторегрессионную функцию. Охарактеризуйте структуру ряда. Выбрать наилучший тип тренда и определить его параметры. Известны сведения об уровне среднегодовых цен на мировых рынках на шерсть из Новой Зеландии, амер. центы за кг.

Год	Цена
1970	73,8
1971	72,6
1972	106,9
1973	237,5
1974	214,7
1975	147,6
1976	202,9
1977	256,4
1978	249,6
1979	300,4
1980	316,7
1981	274,6
1982	239,7
1983	221,9

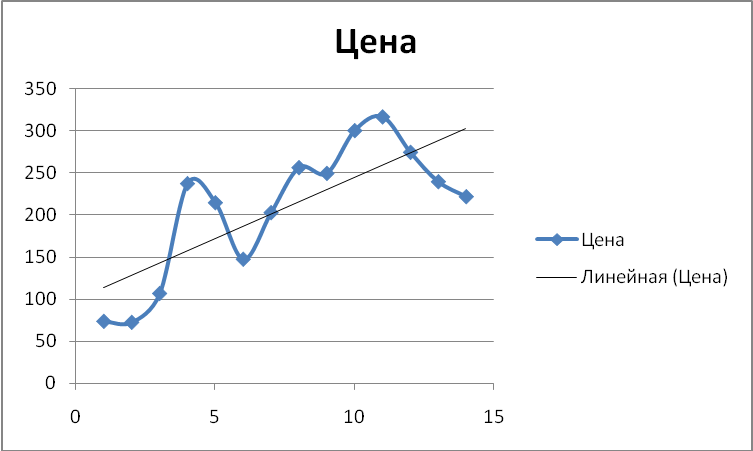
Среднее	208,2357
При T=1	135,6357	При T=2	-5,56429
	101,3357		-266,764
	-29,2643		-221,164
	-6,46429		-86,9643
	60,63571		-197,564
	5,335714		-304,564
	-48,1643		-290,964
	-41,3643		-392,564
	-92,1643		-425,164
	-108,464		-340,964
	-66,3643		-271,164
	-31,4643		-235,564
	-13,6643
	208,2357
Средние	5,271429		-253,248
Коэффициент автокорреляции	0,014485		0,000539

Коэффициент автокорреляции при t=1 выше, чем при t=2, таким образом выбирается авторегрессионная модель при t=1. Анализ автокорреляционной функции позволяет выявить структуру ряда. Т.к. наиболее высоким оказался коэффициент 2-го порядка – то содержит циклические колебания с периодичностью в  моментов времени.

Задание 36

По двадцати предприятиям отрасли была получена следующая матрица парных коэффициентов корреляции показателей: у – объем выпуска продукции (млн.руб.), х1 – численность занятых на предприятии, х2 – среднегодовая стоимость основных фондов

	у	х1	х2
у	1
х1	0,7	1
х2	0,9	0,5	1

Определить частные коэффициенты корреляции результата с каждым из факторов. Прокомментируйте различие полученных парных и частных коэффициентов корреляции.

	у	х1	х2
у	1	0,3	0,1
х1		1	0,5
х2			1

Т.к. частные коэффициенты меньше парных, то наличие других величин преувеличивает связь между признаками.  

Задание 46

Два арбитра оценили мастерство 10 спортсменов, в итоге были получены три последовательности рангов в первой строке приведены ранги арбитра А, во второй – ранги арбитра В:

1	2	3	4	5	6	7	8	9	10
3	10	7	2	8	5	6	9	1	4

Вычислить коэффициент ранговой корреляции Спирмена между результатами тестирования по двум тестам на уровне а=0,05 оценить его значимость.

1	2	3	4		5	6	7	8	9	10
3	10	7	2		8	5	6	9	1	4
-2	-8	-4	2		-3	1	1	-1	8	6
4	64	16	4		9	1	1	1	64	36			200
коэффициент ранговой корреляции Спирмена										-0,2121212
F-статистика	Уровень значимости			F(gama,1,n-2)	Решение
-1,75	0,05			5,12	не значима
Уровень значимости	0,05			t(gamma,n-2)	2,23

При использовании коэффициента ранговой корреляции теснота связи между признаками оценивается как слабая, т.к. значение коэффициента равные 0,3. Что подтверждают тесты на значимость.

Задание 56

Имеются данные об уровне дивидендов, выплачиваемых по обыкновенным акциям (%) в сопоставимых ценах за девять лет:

Год	1	2	3	4	5	6	7	8	9
Дивиденды по обыкновенным акциям	4,2	3	2,4	2	1,9	1,7	1,8	1,6	1,7

Найти среднее квадратическое отклонение, коэффициент автокорреляции для лагов τ=1,2

Среднее	2,255556
Дисперсия	0,725278
СКО	0,851632
R(1)	0,810073
R(2)	0,326624

При анализе временного ряда дивидендов наиболее высоким оказался коэффициент автокорреляции уровней первого порядка. Следовательно, исследуемый ряд содержит только тенденцию.

Задание 62

Для модели протекционизма Сальватора

M_t=a₁+b₁₂N_t+b₁₃S_t+b₁₄E_t-1+b₁₅M_t-1+ε₁

N_t=a₂+b₂₁M_t+b₂₃S_t+b₂₆Y_t+ ε₂

S_t=a₃+b₃₁M_t+b₃₂N_t+b₃₇X_t+ ε₃

Где Y – рельный ВВП

M – доля импорта в ВВП

N – общее число прошений об освобождении от таможенных пошлин

S – число удовлетворенных прошений об освобождении от таможенных пошлин

Ε – фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 для всех остальных лет

X – реальный объем чистого экспорта

t – текущий период

t-1 – предыдущий период

1. Применив необходимое и достаточное условие идентификации, определите, идентифицировано ли каждое из уравнений модели

Первое уравнение: Н – эндогенные переменные – 3 ; D – экзогенные переменные – 2. Точно идентифицируемо ,т.к. Н= D+1

Второе уравнение: Н – эндогенные переменные – 3 ; D – экзогенные переменные – 1.

Третье уравнение: Н – эндогенные переменные – 3 ; D – экзогенные переменные – 1

Второе и третье уравнения не идентифицируемы ,т.к. Н>D+1

2. Определите метод оценки параметров модели

Т.к. уравнения идентифицированы Оценка сверхидентифицированного уравнения осуще­ствляется при помощи двухшагового метода наименьших квадратов.

3. Запишите приведенную форму модели.

На основе системы приведенных уравнений по точно идентифицированному первому уравнению определим теоретические значения эндогенной переменной М. Для этого в приведенное уравнение M_t=a₁+b₁₂N_t+b₁₃S_t+b₁₄E_t-1+b₁₅M_t-1+ε₁

Подставим значения, имеющиеся в условии задачи. Х-экзогенные переменные, у – эндогенные

Y_t= a₁+b₁₂Y_t2+b₁₃Y_t3+b₁₄X_t-1+b₁₅Y_t-1+ε₁

Y_t2=a₂+b₂₁Y_t+b₂₃Y_t3+b₂₆Y_t4+ ε₂

Y_t3=a₃+b₃₁Y_t+b₃₂Y_t2+b₃₇Y_t4+ ε₃

13