Действия над числами, полученными от измерения величин

Действия над числами, полученными в результате измерения величин, подчиняются тем же законам, что и действия над числами в пределах 10, 100, 1000 и многозначными числами.

Действия над числами, полученными от измерения величин, опираются на знание учащимися единиц измерения и их соотношений, а также умение выразить одни меры через другие.

Основные ошибки, которые допускают младшие школьники при выполнении арифметических действий со значениями величин:

30 см +5 мм = 35 см (или 35 мм)

25 см – 5 мм =20 см (или 20 мм)

1 м 5 см • 3=45 см

45 грн.:6 =7 (ост. 3)

Часто учащиеся принимают во внимание только числовые значения и не учитывают наименований: наименования они либо пишут произвольно, либо опускают совсем. Это свидетельствует о том, что учащиеся не понимают, что при изменении единиц измерения величин изменяются наименование и числовая характеристика величины, сама же величина остается неизменной.

Особенно много ошибок учащиеся допускают в действиях над числами, в которых число разрядных единиц равно нулю.

6 грн. 8 к.+5 грн. 7 к. =12 грн. 5 к. (10 к. превратили в 1 грн.),

2 км 6 м –1 км 8 м =1 км 8 м.

При изучении этой темы важно не только исправлять, но и предупреждать ошибки учащихся.

При изучении сложения и вычитания чисел, полученных от измерения величин, важно соблюдать определенную последовательность. Всегда решение примера надо начинать с его предварительного анализа.

Сложение и вычитание

Действия над числами, полученными от измерения величин, выполняются так же, как действия над многозначными числами, с той лишь разницей, что при числах должны быть записаны наименования единиц измерения.

1) Сначала рассматриваются те случаи сложения и вычитания чисел, выражающих длину, массу, стоимость, в которых не требуется производить замену одних единиц измерения другими.

8 м + 7 м; 15 м – 7 м; 65 см + 27 см; 92 см – 27 см

2) Затем рассматриваются действия над числами с разными единицами измерения. Выполнять действия над ними можно разными способами:

а) Заменить крупные меры мелкими, т. е. выразить компоненты действий в одних и тех же единицах, например:

5 дм+4 см=? 5 дм=50 см, 50 см+4 см =54 см =5 дм 4 см.

Значит, 5 дм+4 см =5 дм 4 см

5 м+75 см =5 м 75 см

50 к.+2 грн.=2 грн. 50 к.

б) Показать, что при сложении, например, двух полосок длиной соответственно 5 дм и 4 см в сумме получится полоска длиной 5 дм 4 см; если взять 50 к, и 2 грн., то всего денег будет 2 грн. 50 к.

Аналогично объясняется и действие вычитания:

5 дм 4 см – 4 см; 5 дм 4 см–5 дм; 7 грн. 50 к.–7 грн.; 7 грн. 50 к.–50 к.

8 м 67 см – 5 м; 8 грн. 67 к.–38 к.

а) Можно решать эти примеры устно путем рассуждении: если из 7 грн. 50 к. вычесть 7 грн., то останется только 50 к.

б) Можно раздробить крупные меры в мелкие:

7 грн. 50 к.=750 к. 7 грн.=700 к., 750 к.–700 к.=50 к.

в) Можно решить примеры письменно с записью в столбик:

3) 5 дм 3 см+1 дм 4 см

5 грн. 70 к. + 3 грн. 25 к.

7 дм 4 см – 3 дм 2 см

8 грн. 90 к. – 5 грн. 48 к.

18 км 750 м + 36 км 185 м

27 км 386 м – 15 км 190 м

Решение этого вида примеров можно провести:

а) устно, путем рассуждений: гривни вычитаются из гривень, а копейки – из копеек, т. е. надо складывать и вычитать числа одного наименования;

б) с записью в столбик:

После этого рассматриваются случаи сложения и вычитания чисел, выражающих длину, массу, стоимость, в результате действий над которыми мелкие меры нужно выразить в более крупных.

I.

1) 8 см + 2 см =10 см =1 дм

1 дм–3 см=7 см

2) 75 к.+25 к.=100 к.=1 грн.

1 грн.–85 к.=15 к.

3) 560 м + 440 м =1000 м = 1 км

1 км–350 м=650 м

Решение такого вида примеров проводится устно с записью в строчку или письменно с записью в столбик:

II.

1) 5 см 8 мм+2мм 2) 8 грн. 57 к. + 43 к.

3) 6 км 380 м+620 м

1-й способ решения.

2-й способ решения (крупные меры заменяются мелкими).

III. 1) 8 см –5мм 2) 10 грн.–57 к. 3) 7 т–185 кг

В данном случае, чтобы выполнить вычитание, надо занять одну крупную единицу измерения и заменить ее мелкими единицами. Решать эти примеры можно двумя способами:

1-й способ решения. Заметим, что в уменьшаемом 10 грн. и нет копеек, занимаем 1 грн., остается 9 грн., 1 грн. содержит 100 к., 100 к.–57 к.=43 к. В итоге получим 9 грн. 43 к.

2-й способ решения.

Примеры этого вида можно решать с проверкой сложением.

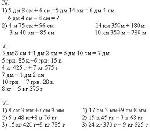
VII. Особые случаи сложения и вычитания.

К особым случаям сложения и вычитания относятся сложение и вычитание чисел, в которых число единиц равно нулю. Характерной ошибкой является вписывание лишних нулей или пропуск их, например: 3 грн. 5 к. = 35 к., или 350 к., или 3 005 к. Это приводит к ошибкам. Предупредить подобные ошибки можно, если в числа вместо пропущенных разрядов вписывать нули: 3 грн. 05 к., 5 кг 075 г, 15 км 007 м, 3 кг 008 г, 1 кг 076 г.

Решение подобных примеров может быть осуществлено одним из вышеуказанных способов. Необходимо постоянно учить детей перед выполнением действий анализировать числа, пример в целом и, только выбрав наиболее рациональный прием решения, приступать к выполнению задания.

Чтобы учащиеся осознанно выполняли задания, необходимо предлагать им такие виды упражнений: самостоятельное составление примеров с числами, имеющими одинаковые единицы измерения, составление примеров, в компонентах которых единицы тех или иных разрядов равны нулю; выбор из ряда примеров и решение только тех примеров, в которых надо вставить нули, и т.д.

Очень важно давать учащимся задания на сопоставление примеров, отличающихся соотношением мер, например:

5 дм 7 см + 4 дм 8 см

5 м 7 см + 4 м 8 см

5 км 7 м + 4 км 8 м

5 км 75 см + 4 км 48 см и т. д.

Полезно поставить вопрос: почему ответы получились разные? Каким бы способом ни производились вычисления, учащиеся должны понимать, что сложение и вычитание чисел, выраженных в мерах длины, массы, стоимости и т.д., выполняются так же, как сложение и вычитание многозначных чисел.