1. Теорема

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Доказательство

Р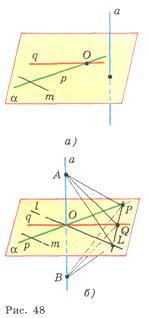 ассмотрим прямую а, которая перпендикулярна к прямым р и q, лежащим в плоскости α и пересекающимся в точке О (рис. 48, а). Докажем, что a ⊥ α. Для этого нужно доказать, что прямая а перпендикулярна к произвольной прямой m плоскости α.    Рассмотрим сначала случай, когда прямая а проходит через точку О (рис. 48, б). Проведем через точку О прямую l, параллельную прямой m (если прямая m проходит через точку О, то в качестве l возьмем саму прямую m). Отметим на прямой а точки А и В так, чтобы точка О была серединой отрезка АВ, и проведем в плоскости а прямую, пересекающую прямые р, q и l соответственно в точках P,Q и L. Будем считатьдля определенности, что точка Q лежит между точками P и L (рис. 48, б).    Так как p и q - серединные перпендикуляры отрезка АВ, то АР=ВР AQ=BQ. Следовательно ΔAPQ=ΔBPQпо трем сторонам. Поэтому ∠APQ =∠BPQ.

Сравним треугольники APL и BPL. Они равны по двум сторонам и углу между ними (АР = ВР, PL — общая сторона, ∠ APL = ∠BPL), поэтому AL=BL. Но это означает, что треугольник ABL равнобедренный и его медиана LO является высотой, т.е. l ⊥ a. Так как l||m и l ⊥ a, то m ⊥ a (по лемме о перпендикулярности двух параллельных прямых к третьей). Итак, прямая а перпендикулярна к любой прямой m плоскости α, т.е. а ⊥ α.

Рассмотрим теперь случай, когда прямая а не проходит через точку О. Проведем через точку О прямую а1, параллельную прямой а. По упомянутой лемме а1 ⊥p и а1 ⊥q, поэтому по доказанному в первом случае а1 ⊥α. Отсюда (по первой теореме п. 16) следует, что а ⊥α. Теорема доказана.

2. Лемма

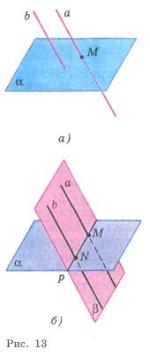Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Доказательство

         Рассмотрим параллельные прямые а и b, одна из которых — прямая а — пересекает плоскость α в точке М (рис. 13, а). Докажем, что прямая b также пересекает плоскость α, т.е. имеет с ней только одну общую точку.     Обозначим буквой β плоскость, в которой лежат параллельные прямые а и b. Так как две различные плоскости α и β имеют общую точку М, то по аксиоме А₃ они пересекаются по некоторой прямой р (рис. 13, б). Эта прямая лежит в плоскости β и пересекает прямую а (в точке М), поэтому она пересекает параллельную ей прямую b в некоторой точке N. Прямая р лежит также в плоскости α, поэтому N — точка плоскости α. Следовательно, N — общая точка прямой b и плоскости α.     Докажем теперь, что прямая b не имеет других общих точек с плоскостью α, кроме точки N. Это и будет означать, что прямая b пересекает плоскость α. Действительно, если бы прямая b имела еще одну общую точку с плоскостью α, то она целиком лежала бы в плоскости α и, значит, была бы общей прямой плоскостей α и β, т.е. совпадала бы с прямой р. Но это невозможно, так как по условию прямые а и b парал­лельны, а прямые а и р пересекаются. Лемма доказана. 

Билет №8.

1. П рямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Теорема

Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Доказательство

Рассмотрим две параллельные прямые а и а1 и плоскость α, такую, что a ⊥ α. Докажем, что и а1 ⊥ α.

Проведем какую-нибудь прямую х в плоскости α (рис. 46). Так как a ⊥ a, то a ⊥ x. По лемме о перпендикулярности двух параллельных прямых к третьей а1 ⊥ x. Таким образом, прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α, т.е. а1 ⊥ α. Теорема доказана.

Теорема.

Если две прямые перпендикулярны к плоскости, то они параллельны

Доказательство

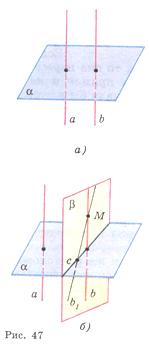
Рассмотрим прямые а и b, перпендикулярные к плоскости α (рис. 47, а). Докажем, что а||b.

Через какую-нибудь точку М прямой b проведем прямую b1, параллельную прямой а. По предыдущей теореме b1 ⊥ α. Докажем, что прямая b1 совпадает с прямой b. Тем самым будет доказано, что а||b. Допустим, что прямые b и b1 не совпадают. Тогда в плоскости β, содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β (рис. 47, б). Но это невозможно, следовательно, а||b. Теорема доказана.

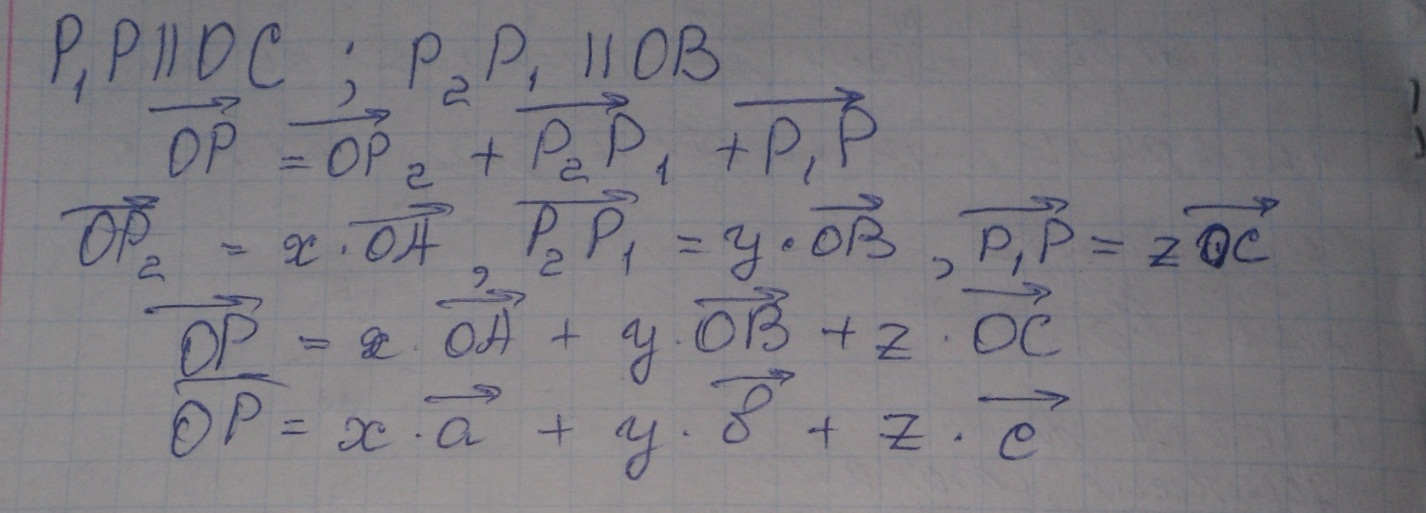
Билет №9.

Б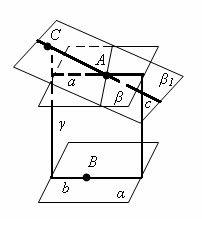 илет № 10.

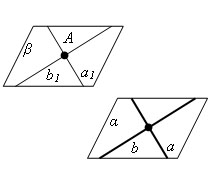
1. Теорема  Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.   Доказательство  Проведем в данной плоскости α какие-нибудь две пересекающиеся прямые a и b. Через данную точку A проведем параллельные им прямые a1 и b1. Плоскость β, проходящая через прямые a1 и b1, по теореме о признаке параллельности плоскостей параллельна плоскости α.    Предположим, что через точку A проходит другая плоскость β1, тоже параллельная плоскости α. Отметим на плоскости β1 какую-нибудь точку С, не лежащую в плоскости β. Проведем плоскость γ через точки A, С и какую-нибудь точку B плоскости α. Эта плоскость пересечет плоскости α, β и β1 по прямым b, a и с. Прямые a и с не пересекают прямую b, так как не пересекают плоскость α. Следовательно, они параллельны прямой b. Но в плоскости γ через точку A может проходить только одна прямая, параллельная прямой b. что противоречит предположению. Теорема доказана.

2. 

Б илет № 11.