1. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Т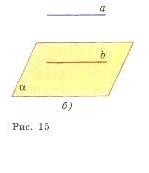 еорема

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Доказательство.

Рассмотрим плоскость α и две параллельные прямые а и b, расположенные так, что прямая b лежит в плоскости α, а прямая а не лежит в этой плоскости (рис. 15, б). Докажем, что a||α.

Допустим, что это не так. Тогда прямая а пересекает плоскость α, а значит, по лемме о пересечении плоскости параллельными прямыми прямая b также пересекает плоскость α. Но это невозможно, так как прямая b лежит в плоскости α. Итак, прямая а не пересекает плоскость α, поэтому она параллельна этой плоскости. Теорема доказана.

2. Дано:  Плоскость α  SO ┴ α SA – наклонная  OA – проекция SA MN принадлежит α

Доказать: MN ┴ SA

Доказательство:

Зададим векторы  ,  ,  ,  .  =   +  Умножим обе части на  :  •   =   •   +   •  Скалярное произведение двух перпендикулярных векторов равно 0:  •   = 0, но   и   не нулевые векторы, значит,   ┴  , прямая оказалась перепендикулярной наклонной, что и требовалось доказать.

Б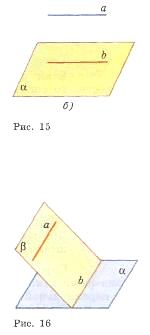 илет №6.

1. Прямая и плоскость называются параллельными, если они не имеют общих точек

Свойства: 1°. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.    Пусть через данную прямую а, параллельную плоскости α, проходит плоскость β, пересекающая плоскость α по прямой b (рис. 16). Докажем, что b||a. Действительно, эти прямые лежат в одной плоскости (в плоскости β) и не пересекаются: ведь в противном случае прямая а пересекала бы плоскость α, что невозможно, поскольку по условию a||α.  

 2°. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.    В самом деле, пусть а и b — параллельные прямые, причем прямая а параллельна плоскости α. Тогда прямая а не пересекает плоскость α, и, следовательно, по лемме о пересечении плоскости параллельными прямыми прямая b также не пересекает плоскость α. Поэтому прямая b либо параллельна плоскости α, либо лежит в этой плоскости. 

2)

З адача

   Доказать, что через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.

Решение

Обозначим данную прямую буквой а, а произвольную точку пространства — буквой М. Докажем, что существует плоскость, проходящая через точку М и перпендикулярная к прямой а.    Проведем через прямую а две плоскости α и β так, чтобы М ∈ α (рис. 49) . В плоскости α через точку Мпроведем прямую р, перпендикулярную к прямой а, а в плоскости β через точку пересечения прямых р и апроведем прямую q, перпендикулярную к прямой а. Рассмотрим плоскость γ, проходящую через прямые р иq. Плоскость γ является искомой, так как прямая а перпендикулярна к двум пересекающимся прямым р и qэтой плоскости.

Билет №7.