4 Обработка данных методами регрессионного анализа

4.1 Теоретическое введение

4.1.1 Оценка коэффициентов регрессии

Важной задачей математической статистики является получение функциональной зависимости одной величины (y) от другой (x) по результатам эксперимента. Будем считать, что функциональная зависимость между величинами, называемая в дальнейшем моделью, известна из предварительных сведений с точностью до параметров β₁, β₂, ..., β_m и имеет вид

y = f (x, β1, β2, ..., βm ).

(4.1)

Для отыскания неизвестных параметров проведено n наблюдений (x_i, Y_i ), i = 1, 2, ..., n. Но так как результаты наблюдений не свободны от погрешностей измерений, которые мы будем рассматривать как случайные ошибки, то по ним нельзя точно найти искомые параметры. Поэтому приходится ставить задачу об отыскании не значений параметров, а их оценок по результатам эксперимента.  Будем предполагать, что значения аргументов x_i известны точно, а значения функции Y_i – взаимно независимые случайные величины, включающие случайные ошибки Z_i , ­ ­т.е. Y_i = f(x_i, β₁, β₂, ..., β_m ) + Z_i , ­ ­где  M (Z_i ) = 0; ­ ­ ­ ­ ­D(Z_i ) = D(Y_i ) = σ².  Здесь мы предполагаем, что измерения равноточны. В дальнейшем будет рассмотрен более общий случай.  Для оценок параметров β₁, β₂, ..., β_m используется метод наименьших квадратов. В качестве оценок этих параметров принимаются значения  , при которых имеет минимум функция

(Yi – f (xi, β1, β2, ..., βm ))2.

(4.2)

Уравнение (4.1) называется уравнением регрессии, а отыскание оценок параметров и исследование получаемых моделей – регрессионным анализом.  Будем рассматривать уравнения регрессии, линейные относительно оцениваемых параметров β₁, β₂, ..., β_m :

f (x, β1, β2, ..., βm ) = β1φ1(x) + β2φ2(x) + ... + βmφm(x).

(4.3)

Функции φ₁(x), φ₂(x), ... , φ_m(x) называются базисными функциями, их рассматривают на множестве точек (x₁, x₂, ..., x_n ), где n – число экспериментов.  Формулы для оценки параметров регрессионной модели (4.3) значительно упрощаются, если базисные функции ортогональны, т.е. их скалярные произведения (φ_j , φ_k ) =  φ_j(x_i)φ_k(x_i) равны нулю для любых ­ j ≠ k.  Обозначим ортогональные базисные функции T₁(x), T₂(x), ..., T_m(x) и функцию регрессии в ортогональном базисе:

y = B1T1(x) + B2T2(x) + ... + BmTm(x).

(4.4)

Тогда оценки параметров регрессии определяются по формуле

.

(4.5)

Оценки параметров регрессии в ортогональном базисе обладают следующими свойствами.  1. Каждая оценка   находится только по «своей» базисной функции T_j и не зависит от остальных, что создает удобства при «достраивании» регрессионных моделей.  2. Каждая оценка   является несмещенной оценкой истинного значения параметра B_j , т.е. M( ) = B_j .  3. Отклонения ΔY_i = Y_i –  (x_i) экспериментальных результатов Y_i от рассчитанных по оценкам (1.63) значений   ортогональны всем базисным функциям T₁(x), ...,T_m(x), использованным в регрессионной модели:

(ΔY, Tj ) =  ΔYi·Tj(xi ) = 0,

(4.6)

что используется для контроля правильности проведенных вычислений.  Перейти от произвольного базиса φ₁(x), φ₂(x), ..., φ_m(x) к ортогональному можно следующим образом. Положим, что T₁(x) = φ₁(x), ­ ­ T₂(x) = φ₂(x) + λ₂T₁(x) и определим коэффициент λ₂из условия ортогональности: (T₂, T₁) = (φ₂, T₁) + λ₂(T₁, T₁) = 0, откуда

λ2 = – (φ2, T1 ) / (T1, T1 ).

(4.7)

Далее положим T₃(x) = φ₃(x) + λ₃T₁(x) + μ₃T₂ (x) и найдем коэффициенты λ₃ и μ₃ из двух условий ортогональности:  (T₃, T₁) = (φ₃, T₁) + λ₃ (T₁, T₁) + μ₃(T₂, T₁) = 0,  (T₃, T₂) = (φ₃, T₂) + λ₃ (T₁, T₂) + μ₃ (T₂, T₂) = 0,  откуда

λ3 = – (φ3, T1) / (T1, T1), ­ ­ ­ μ3 = – (φ3, T2) / (T2, T2).

(4.8)

Рассмотрим более общий случай, когда результаты измерений Y_i неравноточны, т.е. дисперсии величин Y_i различны. Будем полагать в (4.2):

D (Yi) = D (Zi) = σ2 / Wi ,

(4.9)

где W_i – известные веса измерений. В этом случае в методе наименьших квадратов (1.60) минимизируется функция:

(Yi – f (xi, β1, β2, ..., βm ))2Wi ,

(4.10)

скалярное произведения функций определяется следующим образом:  (φ_j , φ_k ) =  φ_j (x_i ), φ_k (x_i) W_i ,  и оценки параметров регрессии в ортогональном базисе находят по формуле

.

(4.11)

Линейную и квадратичную регрессионные модели будем записывать в разложении по ортогональным многочленам для множества точек x₁, x₂, ..., x_n с весами W₁, W₂, ..., W_n ; ортогональные многочлены степеней 0, 1, 2 рассчитываются по формулам  T₁ = 1; ­ ­ ­ T₂ = X; ­ ­ ­ T₃ = X ² + μX + ν,  где Х – кодированное значение аргумента :

,

(4.12)

а коэффициенты μ и ν вычисляются по следующим формулам соответственно:

.

(4.13)

Веса измерений используются и в том случае, когда экспериментальные значения y являются независимыми и равноточными, но для некоторых значений аргумента x_i измерения проводятся несколько раз, т.е. дублируются. Пусть в точке x_i эксперимент дублируется n_i раз, результаты этого дублирования обозначим Y_{i j} ( j = 1, 2, ..., n_i ). Среднее арифметическое результатов эксперимента в точке x_i обозначим Y_i =  Y_{i j} / n_i . Если измерения Y_{i j} равноточны, т.е. D(Y_{i j} ) = σ², то дисперсии средних арифметических равны

D(Yi ) = σ2 / ni .

(4.14)

В этом случае построение регрессионных моделей производим по средним значениям Y_i для каждого значения x_i . Значения Y_i в этом случае неравноточны. Сравнивая формулы (4.9) и (4.14), делаем вывод, что весами измерений в этом случае являются числа измерений n_i , т.е. W_i = n_i.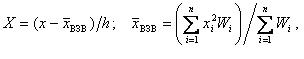