9. Механические колебания. Характеристики колебательного движения. Свободные и вынужденные колебания линейного гармонического осциллятора. Колебания при наличии трении. Резонанс

Колебательное движение материальной точки. Колебательным движением наз-ся движение, обладающее той или иной степенью повторяемости во времени. Если через равн промеж t движ повтор-ся во всех деталях, колеб-я наз периодич-ми, если нет  апериодич-ми. Наиб важны гармонич колеб-я, при кот смещение движ-я точки от полож отсчета измен-ся по зак sin или cos. Если рассматривать тело прикрепленное к пружине, то оно, двигаясь под действием одной лишь упругой силы, испытывает гармонические колебания с постоянной амплитудой и частотой. Это незатухающие (свободные) колебания. Частота таких колебаний наз-ся собственной частотой колебательной с-мы. Она опред-ся внутренними параметрами колеб-й с-мы. Гармонич колеб-я могут возникать не только под действ упр силы, но и любой др, пропорц-ой смещению x и направл к полож-ю равнов-я. Такие силы, опред-щиеся общей формулой , наз-ся квазиупругими.

Разделим обе части уравнения на m и введём обозначение k m = ₀². Тогда получим . Это дифференциальное уравнение второго порядка с постоянными коэффициентами. Чтобы найти кинематический закон движения материальной точки, надо это уравнение проинтегрировать (2-я задача динамики). Путем подстановки различных функций можно убедиться, что решением этого уравнения является гармоническая функция x(t) = Acos(₀t+₀). Амплитуда А и начальная фаза ₀ определяются из начальных условий при t = 0: x(0) = x₀ = Acos₀; (0) = v₀ = –A₀sin₀.

Отсюда амплитуда колебаний 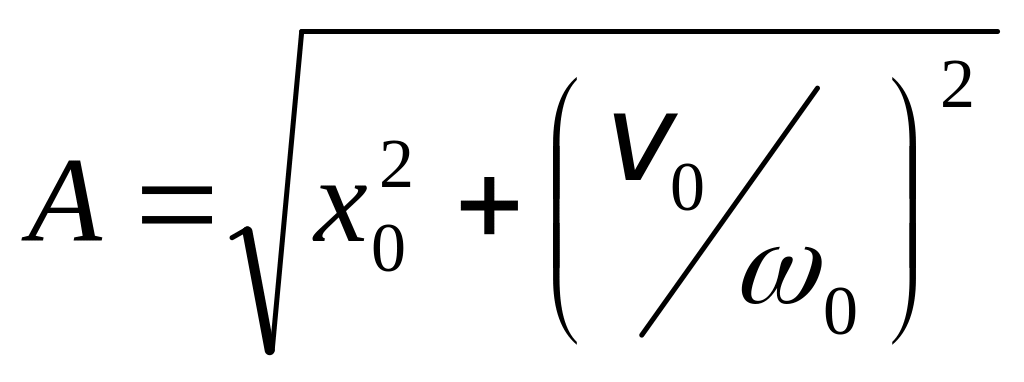; начальная фаза ₀= arctg  . Итак, материальная точка, движущаяся под действием одной лишь упругой силы, испытывает гармонические колебания с постоянной амплитудой и частотой ₀ = . Это незатухающие (свободные) колебания. Частота таких незатухающих колебаний ₀  называется собственной частотой колебательной системы. Она определяется внутренними параметрами колебательной системы. В случае пружинного маятника – это масса груза m и жёсткость пружины k.

М атематический маятник. Это идеализированная колебательная система, состоящая из точечной массы m, подвешенной в однородном гравитационном поле на невесомой и нерастяжимой нити длиной l. Найдём кинематический закон движения математического маятника. На массу m действуют две силы – сила тяжести m и сила натяжения нити . Сумма этих сил направлена по касательной к дуге окружности, по которой может двигаться масса m. Запишем уравнение движения при его естественном задании: m  = – f.

Но f = mg sinα. Отсюда m  = – mg sinα. Смещение по дуге можно представить через угол α. Так как s = lα , то при l = const (нить нерастяжимая)  = l , и уравнение движения в переменных α и t принимает вид: sinα = 0. Если ограничиться малыми углами, то при α < 4 sinα  α c точностью до трёх знаков. В этом случае уравнение движения упрощается: α = 0. Но это – уравнение незатухающих гapмонических колебаний. Кинематический закон колебаний, выраженный через угловое смещение, имеет такой же вид, как и закон колебаний груза на пружине. α = Аcos(₀t+₀). Здесь А – амплитудный угол отклонения нити, ₀ – начальная фаза колебаний.

Циклическая частота колебаний математического маятника аналогично пружинному . Период колебаний T₀ =  . (Формула Гюйгенса,).

Совокупность элем-ов, обеспеч-их колеб движ тела, наз колеб сист-ой. Колеб сист-у, в кот МТ совершает гармонич колеб-я, наз гармонич осциллятором.

Кинетич энергия осциллятора есть энергия движ-я МТ, E_к = . Так как v = = – A₀sin(₀t + ₀), то E_к = sin²(₀t + ₀), или E_к = . (Из формул тригонометрии: cos² = (1 + cos2), sin² = (1 – cos2) )

Кинетич энергия гармонич колеблющегося тела измен с удвоенной частотой 2₀.

Потенц энергия осциллятора есть энергия упруг деформ-и пружины E_п = . Так как x = Acos( ₀t + ₀), то E_п = cos²(₀t + ₀). Но k = m₀². Отсюда

. Потенц энергия гармонич осциллятора также измен-я по гармонич закону с удвоен частотой в противофазе по отнош к кинетич энергии. Полная механич энергия гармонич осциллятора или:

. Когда колеб-я соверш-ся только под действ квазиупругих сил, полная механич энергия осциллятора остаётся пост.

Простейшим типом периодических колебаний являются гармонические колебания. В этом случае или . Первая и вторая производные по времени от x также изменяются по гармоническому з-ну:

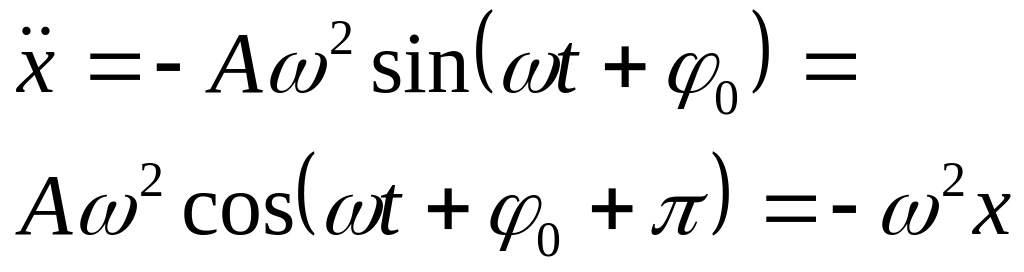
Следовательно, гармонически колеблющаяся величина x удовлетворяет уравнению .

Ур-е колеб с вязким трением. В реал условиях невозм сделать колеб сист-у, в кот бы не было трения. Рассм колеб-я в системе, в кот сила трения пропорц-на скорости движ тела, т.е. , где η– коэфф вязкого сопротивл-я среды. Ур-е движ-я в проекции на ОХ принимает вид: . Так как , получ . Общ вид реш-я этого ур-я завис от соотношения м/у коэфф-ми ₀ и n.

З атух-е периодич колеб-я. Пусть сила упр больше силы вязкого сопротивл-я среды, так что ₀ > n. Реш-е ур-я в этом случе имеет вид: где ,.  можно интерпретировать как амплитуду, завис-ю от t.  время релаксации колеб сист, за кот амплитуда колеб убывает в е раз. Таким. образом, колеб-е тела в вязкой среде при ₀ > n с некот нестрогостью можно характеризовать как колеб-я периодические с пост частотой   и экспоненциально убыв амплитудой. Период затух-их колеб больше периода своб колеб-й, Скорость затух-я колеб-й опред-ют декрементом затух-я , равным отнош любого смещ-я к тому, кот последует через период.   За кажд период T амплитуда и люб смещ-е убывают в одно и то же число раз, равное . ln = nT =  называют логарифмическим декрементом затух-я. - коэфф или показатель затух-я. Если Добротность системы равна разности фаз колеб-й, соотв-ей уменьш-ю энергии колеб-ой сист в е раз.

Если силы трения настолько велики, что ₀< n, то ф-я, опис-ая колеб-я, уже не явл периодич-ой. Колеб-я при больших силах трения неповторяющиеся. Колеблющ-я тело проходит через полож равнов-я не более 1 раза. Такие колеб назыв апериодич-ми.

При затух-их колеб-ях механич энергия сист постеп перех в тепло, во внутр энергию сист-ы. Происх диссипация энергии.

Вынужд колеб-я. Это колеб-я, кот тело совершает при действии на него 3 сил: квазиупругой – kx, вязкого трения и гармонической , где F₀–амплитудное знач-е действ-ей силы, –её частота. Ур-е движ-я тела имеет вид: .разделим на m и заменим, получим: . Реш-е этого ур-я сост из 2 частей. Его 1-ое слаг представл собой общ реш ур-я, кот описыв затух-е колеб сист. 2-ое слаг опис процесс установл-я вынужд колеб с частотой  .

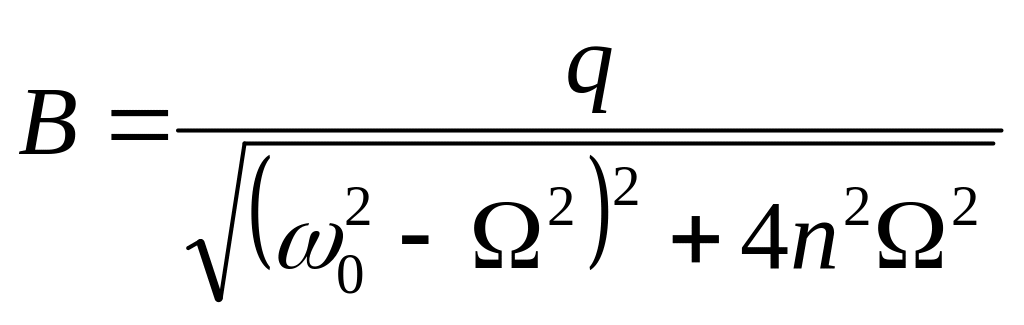Спустя вр t >> собств колеб затухают, и 1-ое слаг устремл-я к 0, а 2-ое слаг выходит на стационарный режим . Здесь амплитуда а сдвиг по фазе опред-я из формулы: .

Резонанс. Я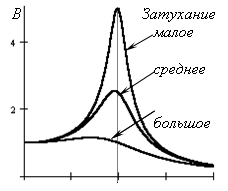 вление резкого возрастания амплитуды вынужденных колебаний системы при приближении циклической частоты возмущающей силы к значению наз-ся резонансом, а величина -резонансной циклической частотой. Кривые зависимости амплитуды от наз-ся резонансными кривыми.

При малом затухании, когда n  0, B_p  , упругие деформации могут превысить допустимые и колебательная система разрушается.

При резонансе вынужд-ая сила соверш макс работу по преод сил вязкого сопротивл среды. Когда резонансная амплитуда стабилизир-ся, работа вынужд-ей силы полностью идёт на преодол-е сил трения, механич энергия сист остается пост.