2.5 План скоростей.

Выполняем построение планов скоростей для первого положения

звеньев механизма. Скорость точки А определим по известной формуле

скорости точки А:

Представим вектор скорости данной точки отрезком = 60 мм, тогда масштаб планов скоростей равен:

Вектор скорости данной точки направлен перпендикулярно кривошипу О₂А в сторону его вращения.

Положение точки В на плане скоростей определим решая векторное уравнение:

где V_A – вектор скорости точки А, известный по величине и направлению;

V_BA – вектор скорости В относительно А, неизвестный по величине, но известный по направлению (перпендикулярно ВА).

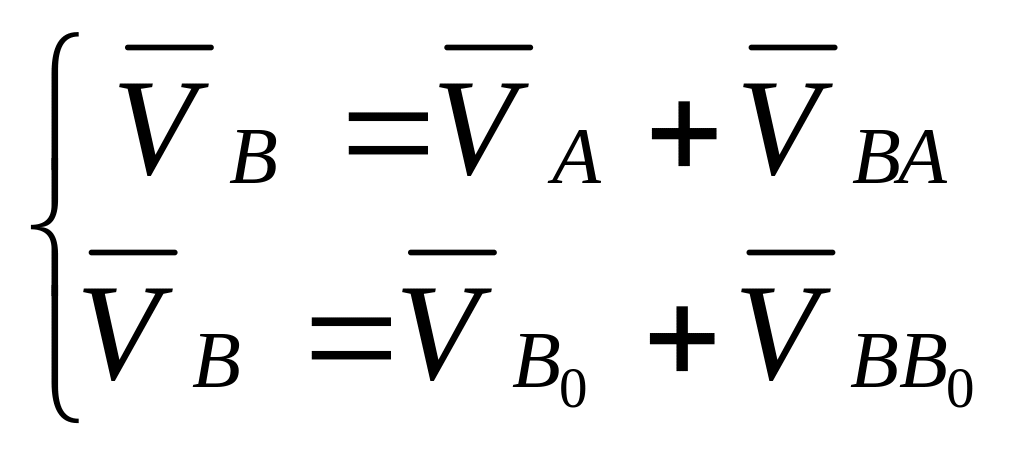
Положение точки C найдем решая графически систему векторных уравнений:

,

где V_С – вектор скорости точки С, неизвестный по величине и направлению;

V_В – вектор скорости точки В, неизвестный по величине и направлению;

V_СВ – вектор скорости С относительно В, неизвестный по величине, но известный по направлению (перпендикулярно СВ).

V_O3 – вектор скорости точки O₃ принадлежащей стойке, V_O3=0;

V_СO3 – вектор скорости С относительно O₃, неизвестный по величине, но известный по направлению (перпендикулярно СO₃).

Воспользуемся теоремой подобия:

мм

Используя построенный план скоростей, определим скорости всех точек механизма.

м/с

м/с

м/с

м/с

м/с

м/с

Угловые скорости звеньев будут равны

с^-1

с^-1

с^-1

с^-1

2.6 План ускорений.

Порядок определения ускорений точек механизма тот же, что и для плана скоростей.

Ускорение точки А относительно точки О₂ определяется только нормальной составляющей ускорения, так как ω₂ – постоянна.

м/с²

Изобразим вектор ускорения точки А на плане ускорений отрезком мм. Тогда масштаб плана ускорений будет равен:

.

Положение точки В на плане ускорений определим решая графически векторное уравнение:

,

где а_В – ускорение точки В, известное только по направлению;

а_А – ускорение точки А известное по величине и направлению;

– нормальное ускорение точки В относительно А, известное по величине и направлению; м/с²;

– касательное ускорение точки В относительно А, известное по направлению (перпендикулярно ВА), но неизвестный по величине.

Положение точки C определим решая графически систему уравнений.

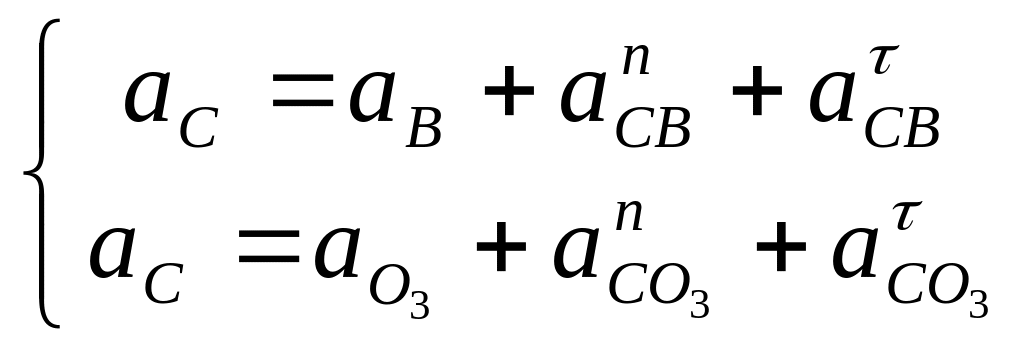
где а_С – ускорение точки С, неизвестное по направлению и величине;

– нормальное ускорение точки С относительно B, известное по величине и направлению (параллельно CB),

м/с²;

– касательное ускорение точки С относительно В, неизвестное по величине, но известное по направлению (перпендикулярно СВ);

– ускорение точки О₃, принадлежащей стойке, =0;

– нормальное ускорение точки С относительно О₃, известное по величине и направлению (параллельно СО₃),

м/с²;

– касательное ускорение точки С относительно О₃, неизвестное по величине, но известное по направлению (перпендикулярно DО₃).

Используя построенный план ускорений, определим длины векторов .

мм

мм

мм

м/с²

м/с²

м/с²

м/с²