1. Генератор постійного струму

Функціональна і принципова схеми електромашинного агрегату на основі генератора постійного струму показані відповідно на рис. 1.1.1, 1.1.2, де позначені: ‑ напруга мережі; U_з, І_з ‑ напруга й струм обмотки збудження генератора LG, ‑ напруга і струм якоря генератора G; ω ‑ частота обертання приводного двигуна М .

Система рівнянь, яка описує динаміку генератора постійного струму в режимі холостого ходу, має вигляд:

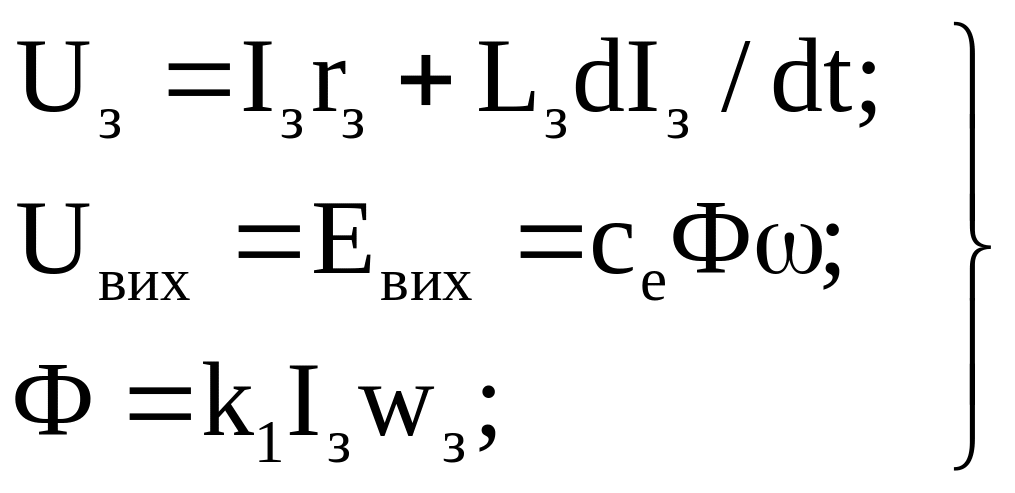(1.1.1)

де r_з, L_з, w_з ‑ відповідно опір, індуктивність і кількість витків обмотки збудження; с_e ‑ конструктивна стала генератора; Ф ‑ магнітний потік одного полюса в зазорі машини; k - коефіцієнт пропорціональності, який зв’язує МРС обмотки збудження з магнітним потоком полюса згідно з характеристикою намагнічування машини Ф(І_зw_з).

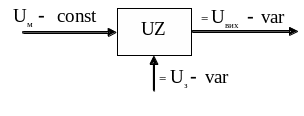
Рис. 1.1.1

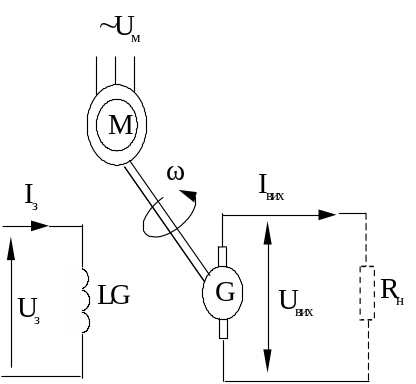
Рис. 1.1.2

Після перетворення рівнянь (1.1.1) отримуємо:

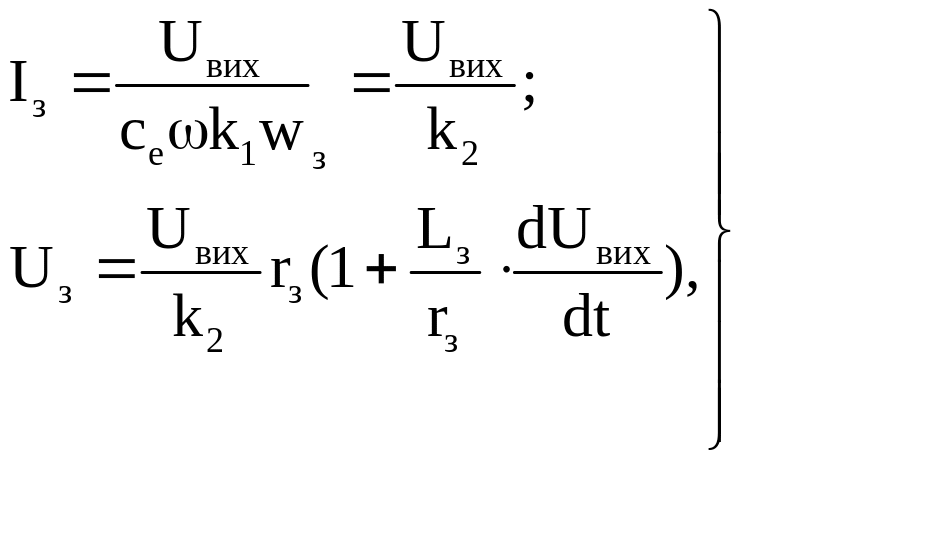(1.1.2)

де k₂ = k₁c_еω w_з.

Позначивши K_г = k₂/r_з, T_з= L_з/r_з і переходячи до зображень, отримуємо передаточну функцію генератора постійного струму для режиму роботи на холостому ході:

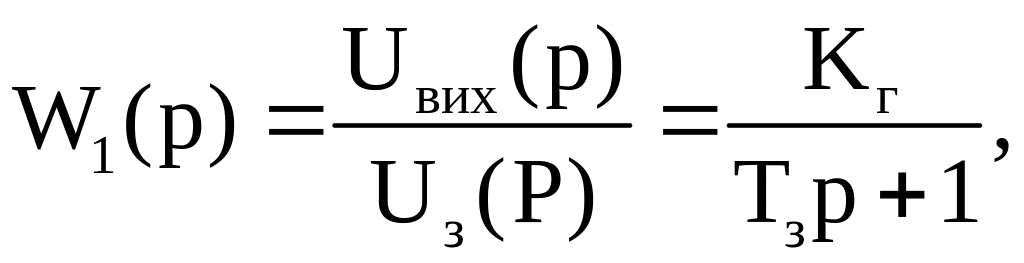(1.1.3)

де K_г ‑ статичний коефіцієнт підсилення генератора, який можна визначити експериментально за характеристикою холостого ходу Е_вих (U_з); T_з ‑ стала часу обмотки збудження генератора.

Отримана передаточна функція (1.1.3) свідчить, що генератор постійного струму в режимі холостого ходу може бути представлений аперіодичною ланкою першого порядку.

Індуктивність обмотки збудження генератора можна визначити експериментально з осцилограми зміни струму збудження при подачі ступінчастої напруги збудження або шляхом розрахунку за характеристикою намагнічування генератора:

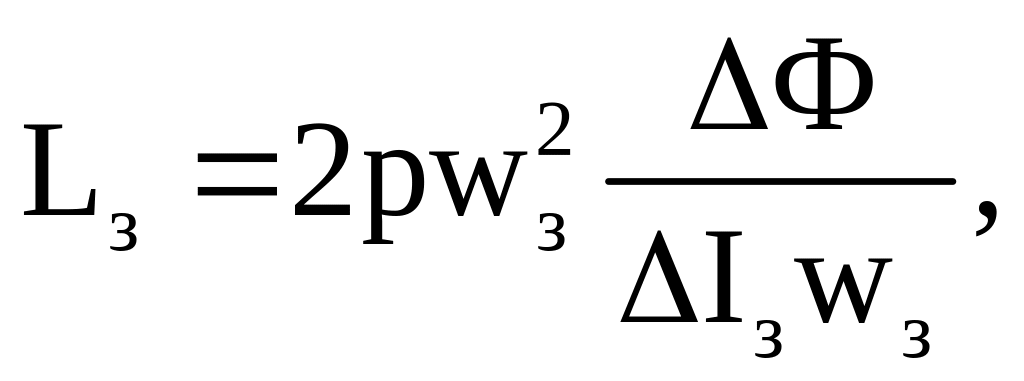
де Ф, І_зw_з ‑ прирости магнітного потоку та МРС поблизу робочої точки на характеристиці намагнічування; р ‑ число пар полюсів.

Отриманій передаточній функції (1.1.3) відповідає структурна схема, показана на рис. 1.1.3.

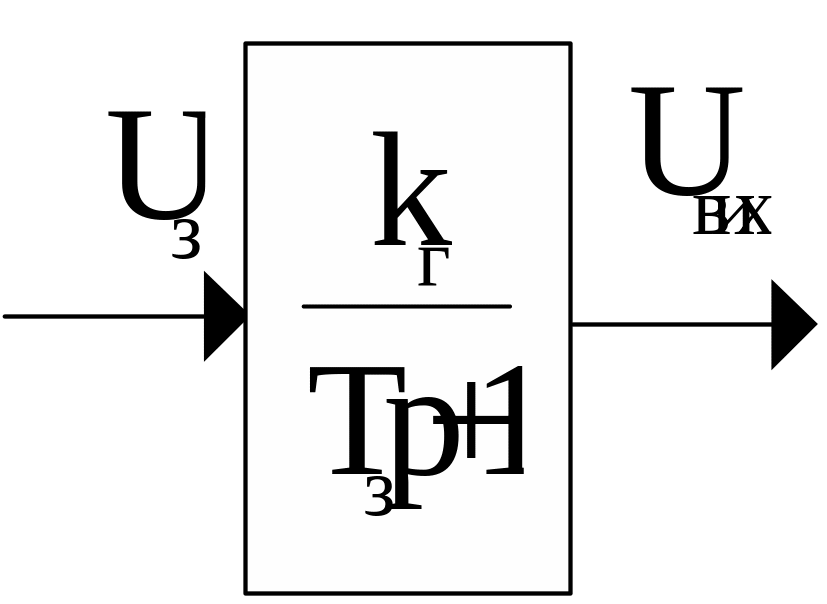
Рис. 1.1.3

При роботі генератора з навантаженням (опір навантаження зображений на рис. 1.1.2 переривчастою лінією), до системи рівнянь (1.1.1) необхідно додати рівняння кола якоря генератора. В цьому випадку

(1.1.4)

де ‑ струм кола якоря генератора; r_яг, L_яг ‑ опір та індуктивність обмотки якоря.

Вихідна напруга генератора при роботі під навантаженням U_вих = І_вихr_н. Тоді рівняння (1.1.1.4) може бути подано у вигляді:

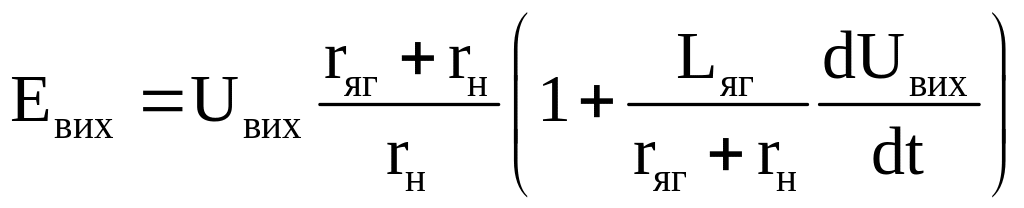
З останнього рівняння, записаного в операторній формі, отримуємо передаточну функцію для кола якоря генератора:

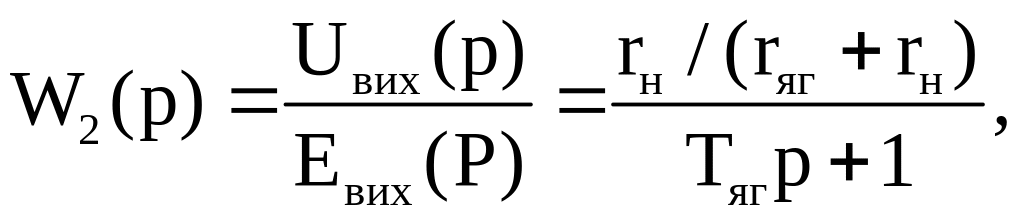(1.1.5)

де ‑ стала часу кола якоря.

Передаточним функціям обмотки збудження (1.1.3) і кола якоря (1.1.5) відповідає структурна схема генератора при його навантаженні (рис. 1.1.4).

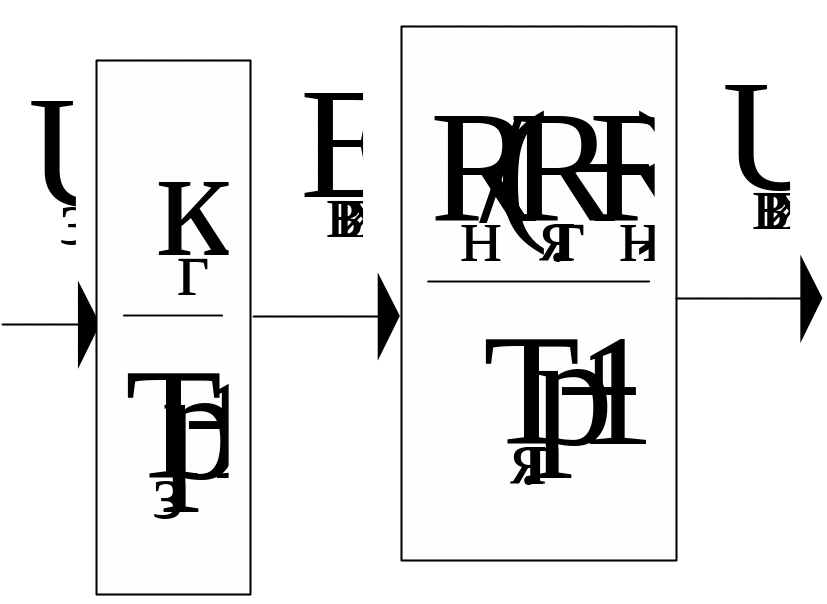
Рис. 1.1.4

В тому випадку, коли за вихідну змінну прийнято струм якоря генератора, передаточна функція кола якоря з урахуванням (1.1.4) буде мати вигляд:

(1.1.6)

Структурна схема генератора, складена згідно з (1.1.3) і (1.1.6), зображена на рис. 1.1.5.

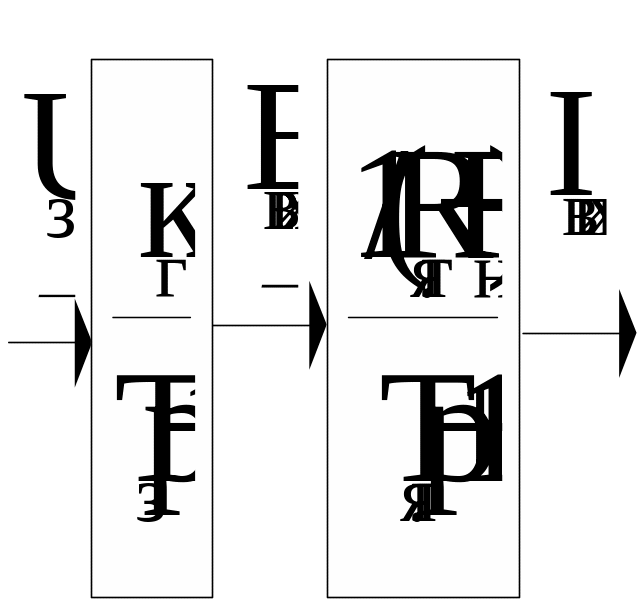
Рис. 1.1.5

Для визначення параметрів передаточних функцій (1.1.5) і (1.1.6) необхідно знати величини і L_яг. Перша з цих величин при відсутності паспортних даних може бути визначена за формулою:

,

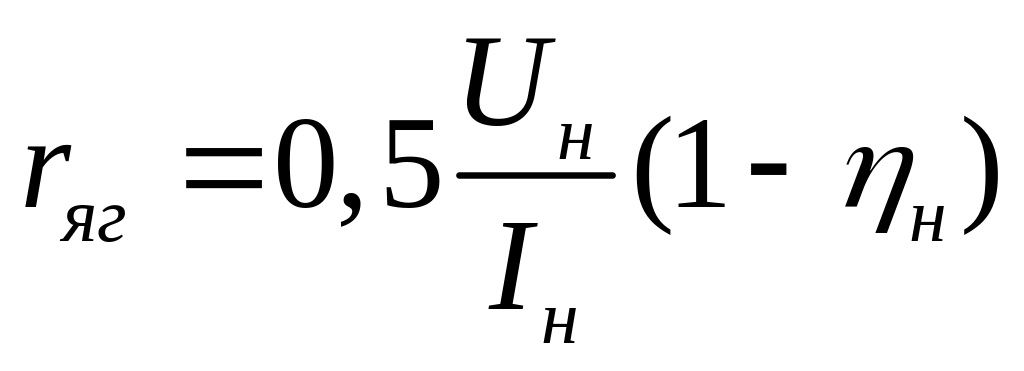де U_н , I_н ‑ номінальні значення, відповідно, напруги і струму якоря генератора; _н ‑ номінальний ККД.

Індуктивність обмотки якоря машини постійного струму орієнтовно можна визначити за формулою Уманського ‑ Лінвілля:

,

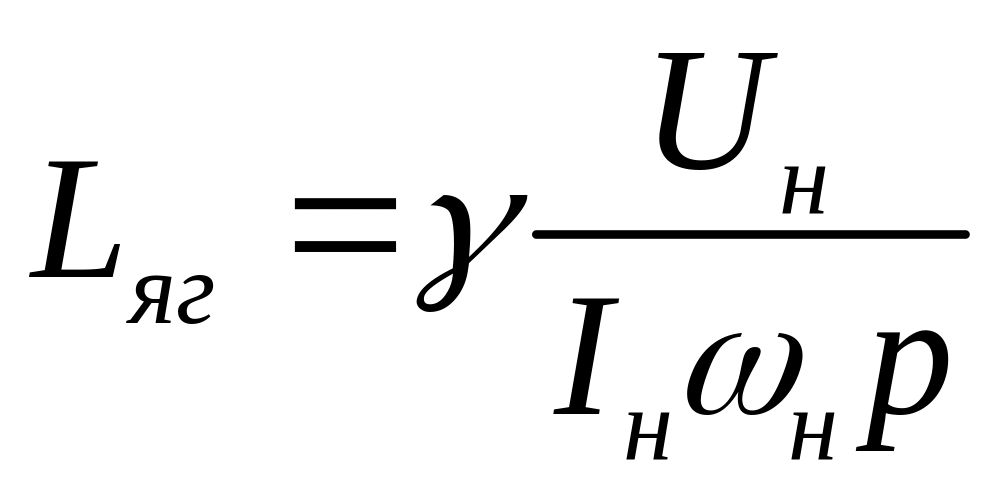де  = 0,6 ‑ для машин без компенсаційної обмотки і  = 0,25 ‑ для машин з компенсаційною обмоткою; _н ‑ номінальна кутова частота обертання машини; p – число пар полюсів якірної обмотки.