1. Д авление

Давление на поверхность равно: где ΔF – сила, действующая на поверхность площадью ΔS.

Давление внутри газа или жидкости можно измерить, помещая туда небольшой куб с тонкими стенками, наполненный той же средой. Поскольку среда покоится, на каждую грань куба со стороны среды действует одна и та же сила ΔF. В окрестности куба давление равно ΔF/ΔS, где ΔS – площадь грани куба.

Внутреннее давление является одним и тем же во всех направлениях, и, во всем объеме независимо от формы сосуда. Этот результат называется законом Паскаля: если к некоторой части поверхности, ограничивающей газ или жидкость, приложено давление P₀, то оно одинаково передается любой части этой поверхности.

Вычислим давление, оказываемое газом на одну из стенок сосуда. Обозначим: n – концентрация молекул в сосуде; m₀ – масса одной молекулы. Движение молекул по всем осям равновероятно, поэтому к одной из стенок сосуда, площадью S подлетает в единицу времени молекул, где – проекция вектора скорости на направление, перпендикулярное стенке.

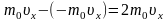
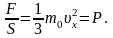
К 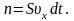аждая молекула обладает импульсом m₀υ_x, но стенка получает импульс (при абсолютно-упругом ударе ) . За время dt о стенку площадью S успеет удариться число молекул, которое заключено в объёме V: Общий импульс, который получит стенка S: Разделив обе части равенства на S и dt; получим выражение для давления

Т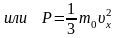 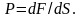аким образом, мы определили давление, как силу, действующую в единицу времени на единицу площади: Наивно полагать, что все молекулы подлетают к стенке S с одной и той же скоростью (рисунок 1.3). На самом деле молекулы имеют разные скорости, направленные в разные стороны, то есть скорости газовых молекул – случайная величина.

Более точно случайную величину характеризует среднеквадратичная величина.

С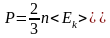 ледовательно, на другие стенки будет точно такое же давление. Тогда можно записать в общем случае: или где Ек – средняя энергия одной молекулы. Это основное уравнение молекулярно-кинетической теории газов. Итак, давление газов определяется средней кинетической энергией поступательного движения молекул.

1.2 Гидростатика

Гидростатика изучает законы равновесия капельных жидкостей.

Силы, действующие в жидкости, подразделяются на объемные (массовые) и поверхностные. Объемные силы пропорциональны объему жидкости , а поверхностные – пропорциональны площади поверхности, на которую они действуют (сила давления на свободную поверхность жидкости в открытом или закрытом сосуде, сила вязкости).

ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ

Жидкость оказывает давление на дно и стенки сосуда, в котором она находится, и на поверхность любого погруженного в нее тела. Рассмотрим некоторую элементарную площадку S внутри объема покоящейся жидкости . Независимо от положения площадки в данной точке объема жидкость будет давить на нее с некоторой силой, равной F и направленной по нормали к площадке, на которую она действует. Ее называют силой гидростатического давления. Отношение F/S представляет собой среднее гидростатическое давление, а предел этого отношения при S→ 0 носит название гидростатического давления в точке, или просто давления:

Р=lim F/S

S→0

где р – гидростатическое давление, Н/м F – сила гидростатического давления, Н; S – элементарная площадка, м

СВОЙСТВА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ

Первое свойство: гидростатическое давление направлено всегда по внутренней нормали к площадке, на которую это давление действует .

Второе свойство: давление в любой точке жидкости одинаково по всем направлениям, поскольку в противном случае также происходило бы перемещение жидкости внутри занимаемого ею объема.

Третье свойство: гидростатическое давление в точке зависит от координат. В жидкости, находящейся только под действием сил тяжести, – от глубины её погружения в жидкость.