Формальне визначення Послідовність дискретних випадкових величин називається ланцюгом Маркова (з дискретним часом), якщо

.Тобто майбутні значення послідовності залежать лише від теперішнього стану і не залежать від минулих.

Матриця  , де називається ма́трицею ймовірностей переходу на  -му кроці, а вектор  , де — початковим розподілом ланцюга Маркова.

Очевидно, матриця ймовірностей переходу є стохастичною, тобто .

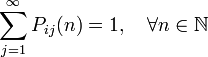Ланцюг Маркова називається однорідним якщо: , або еквівалентно:

для всіх n.

43.**Марківський випадковий процес. Потоки подій. Поток случайных событий

Поток событий — это последовательность однородных событий, наступающих одно за другим в случайные промежутки времени. .

Случайные потоки бывают:

• ординарные: вероятность одновременного появления двух и более событий равна нулю;

• стационарные: частота появления событий λ(t) = const(t);

• без последействия: вероятность появления случайного события не зависит от момента совершения предыдущих событий.

Марковский процесс

Случайный процесс называется марковским процессом (или процессом без последействия), если для каждого момента времени t вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, как система пришла в это состояние.

Марковский процесс удобно задавать графом переходов из состояния в состояние.

Марковский процесс с дискретным временем:

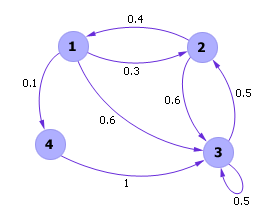
Марковскийпроцесс представим в виде графа, в котором состояния (вершины) связаны между собой связями (переходами из i-го состояния в j-е состояние), см. рис. 33.1. Каждый переход характеризуется вероятностью перехода P_ij. Вероятность P_ij показывает, как часто после попадания в i-е состояние осуществляется затем переход в j-е состояние. Если измерить частоту переходов за достаточно большое время, то эта частота будет совпадать с заданной вероятностью перехода. у каждого состояния сумма вероятностей всех переходов должна быть всегда равна 1.

Реализация марковского процесса представляет собою цепи переходов из

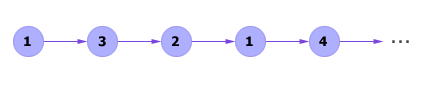
44. **Пуассонівський випадковий процес.

Заданы: полное вероятностное пространство и произвольное множество вида или . Рассмотрим измеримое отображение , индуцирующее вероятностное пространство , где – -алгебра борелевских множеств из , – вероятность, заданная на .

Случайным процессом называется:

1). Если вероятность числа событий на интервале зависит только от и не зависит от положения интервала на временной оси, то такой случайный процесс обладает свойством стационарности.

2). Если события, происходящие на непересекающихся интервалах времени суть независимые случайные величины, то такой случайный процесс обладает свойством отсутствия последствия.

3). Если вероятность того, что в малом интервале времени произойдет не более одного события, есть величина бесконечно малая порядка при , то случайный процесс обладает свойством ординарности.

4). Поток событий , удовлетворяющий условиям: стационарности, отсутствия последействия и ординарности называется пуассоновским, или простейшим.

5). Пуассоновский процесс является непрерывным процессом с дискретным временем.

Свойства: Пуассоновский случайный процесс.

1). Простейший поток событий описывается одномерным распределением 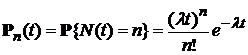, . Параметр называется интенсивностью пуассоновского потока событий.

2). Простейший поток событий описывается многомерным распределением и характеризуется интенсивностью .

3). Пусть ( , ) – моменты появления пуассоновских событий. Тогда случайные величины независимы в совокупности и .

4). Все траектории пуассоновского процесса представляют собой непрерывные монотонные функции.

5). Траектории пуассоновского процесса могут содержать конечное множество точек разрыва второго рода.