14. Ймовірність появи хоча б однієї випадкової події. Задача про товсту монету.

Вероятность появления хотя бы одного события.

Теорема.Вероятность появления хотя бы одного из попарно независимых событий

А₁, А₂,…, А_п равна р (А) = 1 — q₁q₂…q_n , (2.9)

где q_i — вероятность события , противоположного событию А_i .

Доказательство.

Если событие А заключается в появлении хотя бы одного события из А₁, А₂,…, А_п, то события А и  противоположны, поэтому по теореме 2.2 сумма их вероятностей равна 1. Кроме того, поскольку А₁, А₂,…, А_п  независимы, то независимы и , следовательно, р() = . Отсюда следует справедливость формулы (2.9).

Задача про товсту монету 

Какой толщины должна быть монета, чтобы вероятность падения на ребро равнялась бы 1/3?

Для решения этой задачи нужно знакомство с принципом симметрии.

Решение задачи

Для решения задачи нам понадбится следующий результат. Поверхность куска сферы, заключенного между двумя паралельными плоскостями, пропорциональна расстоянию между этими плоскостями, так что толщина нашей монеты должна составлять 1/3 диаметра сферы. Пусть R – радиус сферы, а r – радиус монеты. Согласно теореме Пифагора:

Итак высота ребра монеты составляет около 35% ее диаметра

15.Формула повної ймовірності. Формула Бейеса.

1.Формула повної ймовірності

Ймовірність події А, яка може настати лише за умови появи однієї із попарно не сумісних подій повної групи Н, визначається за формулою:

Р(А)=Р(Н₁)Р _H1(А)+Р(Н₂)Р_H2(А+…+Р(Н_n)Р_Hn(А), або Р(А)=∑Р(H_i)Р_Hi(А).

Формула називається формулою повної ймовірності. Події Ні називають гіпотезами; Р(Ні) – ймовірність гіпотез

2.Формула Байеса Формула повної ймовірності дає можливість встановити ймовірність появи події А, не виясняючи,яка з подій Н викликала подію А. Але якщо подія А відбулася, то можна зацікавитися питанням вияснення “винуватця”, тобто вияснити ймовірність, того, що подія Ні визвала появу події А.

Теорема. Для будь-якої випадкової події А, для якої Р(А) ≠0, і яка може з’явитись лише за умови появи однієї з попарно несумісних випадкових подій Н1, Н2,…,Нn, що складають повну групу подій, виконується рівність: Р_A(Н_i)=Р(Н_i)Р_Hi(А)/Р(А). Оскільки подія А трапилася з однією із подій групи Н, то ∑Р_A(Н_i)=1.

36. Початкові та центральні моменти. Асиметрія та ексцес.

Для дискретної випадкової величини k–й початковий момент визначається за формулою

Для неперервної випадкової величини k–й початковий момент визначається за формулою

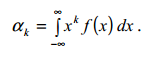
Визначення 4.11. Відхилення випадкової величини від математичного сподівання називають центрованою випадковою величиною. Визначення 4.12. Центральним моментомs-го порядку µs називають математичне сподівання s-го степеня центрованої випадкової величини

Для дискретної випадкової величини s–й центральний момент визначається за формулою

Для неперервної випадкової величини s–й центральний момент визначається за формулою

Оцінку відхилення емпіричного розподілу від нормального проводять за допомогою таких статистичних характеристик, як коефіцієнти асиметрії, тобто ступеня скошеності варіаційного ряду розподілу відносно його симетрії вправо або вліво, і гостровершинності – ексцесу. При зміщенні вправо від центру асиметрія матиме додатне число, при зміщенні вліво – від’ємне.

Коефіцієнт асиметрії (As) обчислюється як відношення центрального моменту третього порядку до куба середнього квадратичного відхилення

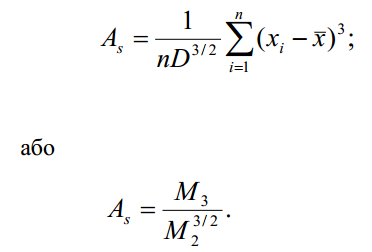
Характер скошеності функції щільності розподілу Р(х) визначається значенням асиметрії As

. При A=0 крива ймовірності р(х) симетрична, при А>0 витягнута її права частина, а при А<0 – ліва частина спаду. Коефіцієнт асиметрії є нормованим моментом третього порядку (µ3) Коефіцієнт ексцесу (англ. Kurtosis) — числова характеристика розподілу ймовірностей дійсної випадкової величини. Коефіцієнт ексцесу характеризує «крутість», тобто, стрімкість підвищення кривої розподілу у порівнянні з нормальною кривою. Ексцесом   (за Фішером) теоретичного розподілу називають характеристику, що обчислюється за наступною формулою: ,

де   — центральний момент четвертого порядку,   — дисперсія.