
- •1. Предмет комбінаторики. Правила суми і добутку. Перестановки без повторення . Перестановки з повтореннями.
- •2.Розміщення без повторення. Розміщення з повтореннями.
- •5. Трикутник Паскаля, біном Ньютона. Число всіх підмножин множини.
- •6.Комбінації з повтореннями.
- •7. Формули включень та виключень; вміти записати для 2 і 3.
- •8.Простір елементарних подій. Операції над подіями. Класичне означення ймовірності. Статистичне означення ймовірності.
- •9.Теорема додавання ймовірностей для несумісних подій. Теорема додавання ймовірностей для сумісних подій.
- •10.Залежні та незалежні події, умовна ймовірність.
- •Умовна ймовірність та її властивість
- •11.Теорема множення для двох випадкових подій. Теорема множення для довільних випадкових подій.
- •12.Попарно залежні та незалежні у сукупності події. Приклад Бернштейна.
- •13.Геометричні ймовірності. Задача про зустріч. Задача Бюффона.
- •14. Ймовірність появи хоча б однієї випадкової події. Задача про товсту монету.
- •15.Формула повної ймовірності. Формула Бейеса.
- •1.Формула повної ймовірності
- •36. Початкові та центральні моменти. Асиметрія та ексцес.
- •37.Приклади: асиметрія показникового розподілу; асиметрія розподілу Пуассона.
- •Розподіл Пуассона
- •38.Теорема Чебишова.
- •39.Теорема Бернуллі
- •40. Центральна гранична теорема.
- •Классическая формулировка ц.П.Т.
- •41. Випадковий процес та його характеристики.
- •42.**Ланцюгі Маркова
- •Формальне визначення Послідовність дискретних випадкових величин називається ланцюгом Маркова (з дискретним часом), якщо
- •43.**Марківський випадковий процес. Потоки подій. Поток случайных событий
- •Марковский процесс
- •Марковский процесс с дискретным временем:
- •**Пуассонівський випадковий процес.
- •45. Поняття про генеральну сукупність та вибірку. Емпірична формула розподілу.
- •46. Вибіркові характеристики. Варіаційний ряд, таблиці частот, гістограма.
- •47.Полігон частот. Статистичне та інтервальне оцінювання параметрів розподілу.
- •48. Вибіркове середнє, вибіркова дисперсія. Інтервальні оцінки параметрів розподілу.
- •49.Надійні межі для математичного сподівання у випадку нормального розподілу.
- •50.Статистична гіпотеза та загальна схема її перевірки. Критерій Пірсона.
10.Залежні та незалежні події, умовна ймовірність.
Випадкові події А і В називають залежними, якщо поява однієї з них (А або В) впливає на ймовірність появи іншої.
У противному разі випадкові події А і В називаються незалежними
Умовна ймовірність та її властивість
Якщо ймовірність випадкової події А обчислюється за умови, що подія В відбулася, то така ймовірність називається умовною. Ця ймовірність обчислюється за формулою
![]() ,
,
![]() .
(17)
.
(17)
Аналогічно
![]() ,
,
![]() . (18)
. (18)
1. Р (А / В) = 0, якщо А∩В = .
2. Р (А / В) = 1, якщо А∩В = В.
3. У решті випадків 0 < Р(А / В) < 1.
11.Теорема множення для двох випадкових подій. Теорема множення для довільних випадкових подій.
Пересечением (произведением) двух событий C и D называется событие F, происходящее тогда и только тогда, когда наступают одновременно оба события C и D: F = C · D
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
![]()
В частности, для независимых событий
![]()
События являются независимыми, если факт появления одного из них не влияет на вероятность появления другого.
12.Попарно залежні та незалежні у сукупності події. Приклад Бернштейна.
Дві події називаються несумісними – якщо їх перетин є неможливою подією. А∩В=V. Дві події називаються сумісними, якщо їх перетин не є неможливою подією. А∩В≠V. Події А1, А2, ..., Аn називаються попарно несумісними, якщо кожні дві з них є несумісними. Приклад: несумісні - В результаті одного підкидання монети не може результатом бути і герб і цифра
Випадкові події А1 , А2 , …, Аn (Аi ( (, i = 1, 2, …, n) називається незалежними в сукупності, якщо при будь-яких k=1, 2, …, n та ( ( і1 ( і2 ( …( іk ( n. Якщо ці рівності виконуються при к=2, то події А1, А2,.., Аn називаються попарно незалежні.
Приклад Бернштейна показує що попарна незалежність подій ще не означає їх незалежність в сукупності.
Підкидається правильний тетраедр, три грані якого пофарбовано відповідно в червоний, синій і зелений кольори, а в розфарбуванні четвертої грані є всі три кольори. Події R (червоний), G (зелений), B(синій) означають, що в розфарбуванні грані, яка стикається з поверхнею, є відповідні кольори. Перевірити, що події R,G,B попарно незалежні, але не незалежні в сукупності.
Розв'язання
Оскільки
тетраедр правильний, то беремо класичну
модель.Кожен колір наявний на двох
гранях, тому .
![]()
Два
і більше кольорів наявні в розфарбуванні
лише однієї грані, тому![]() .Звідси,
.Звідси,
![]()
Тому,
події R,G,B - попарно незалежні за означенням.
Але
![]()
що означає, що вони не є незалежними в сукупності.
13.Геометричні ймовірності. Задача про зустріч. Задача Бюффона.
У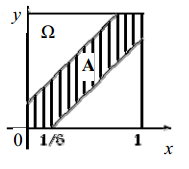 випробуваннях з незчисленною кількістю
результатів для підрахунку ймовірностей
вводять поняття геометричної
ймовірності.
випробуваннях з незчисленною кількістю
результатів для підрахунку ймовірностей
вводять поняття геометричної
ймовірності.
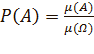 ,
де
,
де ![]() -це
міра області A.
Задача
про зустріч: Дві
особи В і C умовилися зустрітися у
визначеному місці між 14 і 15 годинами
дня. Особа, що прийшла першою чекає другу
впродовж 10 хвилин, після чого вирушає.
Чому дорівнює ймовірність зустрічі цих
осіб, якщо кожна з них може прийти у
будь-який час протягом вказаної години
незалежно від іншої? Розв’язання.
Рахуватимемо інтервал з 14 до 15 годин
дня відрізком [0,1] з довжиною 1 година.
Нехай x і y — моменти приходу В і C (точки
відрізка [0,1]). Всі можливі результати
експерименту – множина точок квадрата
із стороною 1 (рис. 2.2): Ω ={(x, y): 0 ≤ x ≤1, 0
≤ y ≤1}=[0, 1]×[0, 1] .
Можна
вважати, що експеримент зводиться до
кидання точки навмання в квадрат. При
цьому сприятливими результатами є точки
множини А: A={(x, y): x − y ≤1/6} (10 хвилин =
1/6 години). Тобто попадання у множину А
навмання кинутої в квадрат точки U
означає, що В і C зустрінуться. Тоді
ймовірність зустрічі дорівнює
-це
міра області A.
Задача
про зустріч: Дві
особи В і C умовилися зустрітися у
визначеному місці між 14 і 15 годинами
дня. Особа, що прийшла першою чекає другу
впродовж 10 хвилин, після чого вирушає.
Чому дорівнює ймовірність зустрічі цих
осіб, якщо кожна з них може прийти у
будь-який час протягом вказаної години
незалежно від іншої? Розв’язання.
Рахуватимемо інтервал з 14 до 15 годин
дня відрізком [0,1] з довжиною 1 година.
Нехай x і y — моменти приходу В і C (точки
відрізка [0,1]). Всі можливі результати
експерименту – множина точок квадрата
із стороною 1 (рис. 2.2): Ω ={(x, y): 0 ≤ x ≤1, 0
≤ y ≤1}=[0, 1]×[0, 1] .
Можна
вважати, що експеримент зводиться до
кидання точки навмання в квадрат. При
цьому сприятливими результатами є точки
множини А: A={(x, y): x − y ≤1/6} (10 хвилин =
1/6 години). Тобто попадання у множину А
навмання кинутої в квадрат точки U
означає, що В і C зустрінуться. Тоді
ймовірність зустрічі дорівнює
З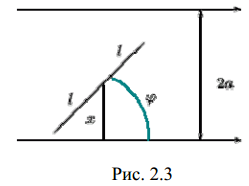
 адача
Бюффона:
На площині накреслені паралельні прямі,
що знаходяться одна від одної на відстані
2a . На площину навмання кинута голка
довжина якої 2l < 2a . Яка ймовірність
того, що голка пересіче одну з прямих?
Розв’язання.
Зрозуміємо, що означає тут “навмання
кинута голка”. Усі можливі положення
голки (відрізки) на площині повністю
визначаються положенням середини голки
і кутом повороту голки відносно
якого-небудь напряму. Причому дві ці
змінні (положення центру і кут повороту)
міняються незалежно один від одного
(рис. 2.3).
Позначимо через x ∈[0,a]
відстань від середини голки до найближчої
прямої, а через ϕ ∈[0,π
] — кут між якимсь напрямом прямих і
голкою. Множина положень голки цілком
визначається вибором навмання
точки
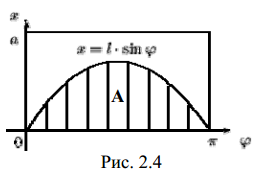
з прямокутника Ω = [0,π ]×[0,a]. (рис. 2.4).
Голка пересікає найближчу пряму, якщо
координати вибраної навмання точки
задовольняють нерівності: x < l ⋅sinϕ
.
адача
Бюффона:
На площині накреслені паралельні прямі,
що знаходяться одна від одної на відстані
2a . На площину навмання кинута голка
довжина якої 2l < 2a . Яка ймовірність
того, що голка пересіче одну з прямих?
Розв’язання.
Зрозуміємо, що означає тут “навмання
кинута голка”. Усі можливі положення
голки (відрізки) на площині повністю
визначаються положенням середини голки
і кутом повороту голки відносно
якого-небудь напряму. Причому дві ці
змінні (положення центру і кут повороту)
міняються незалежно один від одного
(рис. 2.3).
Позначимо через x ∈[0,a]
відстань від середини голки до найближчої
прямої, а через ϕ ∈[0,π
] — кут між якимсь напрямом прямих і
голкою. Множина положень голки цілком
визначається вибором навмання
точки
з прямокутника Ω = [0,π ]×[0,a]. (рис. 2.4).
Голка пересікає найближчу пряму, якщо
координати вибраної навмання точки
задовольняють нерівності: x < l ⋅sinϕ
. ![]() .
Оскільки μ(Ω) = a ⋅π
, то шукана ймовірність дорівнює
.
Оскільки μ(Ω) = a ⋅π
, то шукана ймовірність дорівнює  .
.
