
- •1. Методы лабораторного определения сопротивляемости грунтов.
- •2. Сущность оценки сопротивляемости сдвигу грунтов по теории порового давления к. Терцаги.
- •3. Основные положения теории плотности-влажности Маслова.
- •4. Классификация глинистых грунтов по сопротивляемости сдвигу в соответствии с теорией плотности-влажности Маслова.
- •5. Взаимосвязь параметров сопротивляемости сдвигу грунтов, определенных по теории порового давления Терцаги и плотности-влажности Маслова.
- •7. Сопротивляемость сдвигу сыпучих грунтов. Формула и график функции.
- •9. Учет влияния влажности на показатели сопротивляемости сдвигу глинистых грунтов.
- •10.Способы разделения общего сцепления Cw на сцепление связности Σw и жесткое структурное сцепление Сс.
- •11.Какие факторы определяют прочность сыпучих грунтов
- •12.Прочность скальных (в монолите) грунтов. Метод определения.
- •13.Как изменяется величина угла сопротивления сдвигу при увеличении нагрузки
- •14. Почему сдвиговая прочность глинистых грунтов зависит от влажности, а сыпучих-нет?
- •15. Природа сил жесткого структурного сцепления Сс и связности Ʃw
- •16. Схема компрессионных испытаний грунтов. Цель. Получаемые характеристики: (e), (a), (ep) и (е0)
- •17. Показатели сжимаемости грунта: коэффициент пористости (е), коэффициент уплотнения ( а ), модуль осадки (ер ) и компрессионный модуль деформации (е0).
- •18. Компрессионная характеристика - модуль осадки еp
- •19. Модуль общей деформации грунтов Ер. Как определяется и чем отличается от компрессионного модуля Ео ?
- •20. Как на компрессионной кривой вида в н.Н. Маслова отражается влияние «бытовой» природной плотности грунта основания или предварительного его уплотнения?
- •21. От каких факторов зависит компрессионная сжимаемость грунтов?
- •22. Кривая консолидации глинистых грунтов. Метод ее получения.
- •23. Прогноз изменения влажности и прочности глинистых грунтов во времени в процессе консолидации.
- •24. Условие проявления ползучести пластичных глинистых грунтов
- •25. Условие проявления ползучести скрыто пластичных глинистых грунтов.
- •26. Влияние ползучести на величину показателя консолидации н.Н. Маслова.
- •28 Основные гипотезы напряженного состояния грунтовых оснований сооружений.
- •29. Три фазы работы грунта в основании сооружения. Какие процессы определяют осадку сооружения в каждой фазе?
- •30. Показать роль угла видимости при определении направления и величины главных напряжений.
- •32. Определение касательных и нормальных напряжений в произвольной точке основания и по произвольной площадке с помощью круга мора.
- •33.Оценка прочности основании сооружений без учета нормальных напряжений.
- •34. Оценка прочности основании сооружений с учетом нормальных напряжений.
- •36. Краевая безопасная (Рбез) и допускаемая (Рдоп) нагрузки. Чем они различаются и каким фазам работы грунта основания соответствуют?
- •50.Влияние размера сооружения (ширина фундамента) на величину осадки.
- •51.Какие деформации грунтовых оснований вызывает действие нормальных и касательных напряжений?
- •52.Определение величины конечной осадки сооружения методом послойного суммирования.
- •53.Принцип определения величины активной зоны в методе послойного суммирования при оценке конечной осадки сооружений.
- •54.Критическая нагрузка. Какой фызе работы основания соответствует?
25. Условие проявления ползучести скрыто пластичных глинистых грунтов.
Скрытопластичные глинистые грунты в отличие от пластичной разновидности переходят в состояние длительного деформирования (ползучести) лишь при преодолении касательными напряжениями некоторой определенной величины касательных напряжений τlim (рис. 8.2,), названных Н. Н. Масловым порогом ползучести. Специальными исследованиями было выявлено, что порог ползучести зависит от величины структурного сцепления грунта Сс и угла внутреннего трения φw при той или иной величине плотности-влажности грунта. Величина порога ползучести определяется по зависимости
τlim= p∙tgφw+Cc
Если жесткие структурные связи в глинистом грунте отсутствуют (нарушенная структура), т.е. Сс = 0, зависимость приобретает вид
τlim= p∙tgφw
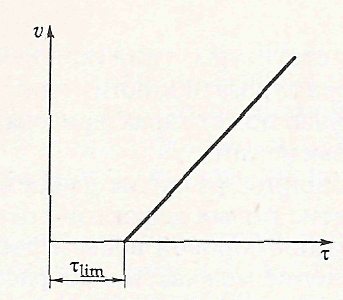
Рис. 8.2.
Зависимость относительной скорости ползучести (течения) от
касательных напряжений для глинистых грунтов:
б — скрытопластичной разновидности
Условия проявления ползучести скрытопластичных глинистых грунтов применительно к величине действующих на грунт касательных напряжений:
τ > τlim= p∙tgφw+Cc
τ > Sw= p∙tgφw+Cc + Σw
Реологическая модель Бингама-Шведов: вязкопластичное тело переходит в состояние вязкопластического течения лишь после преодоления некоторого предельного напряжения сдвига:
Vo =[(τ- τlim) /ŋ]d,
где v0 - скорость перемещения поверхности толщи, имеющей мощность d под воздействием касательного напряжения τ; τlim - величина касательного напряжения, при достижении которой начинается процесс ползучести, именуемая «порогом ползучести»; ŋ - коэффициент вязкости грунта, являющийся характеристикой, отражающей свойства грунта быстрее или медленнее давать деформацию сдвиговой ползучести при прочих равных условиях.
Скрытопластичные глинистые грунты в процессе их ползучести обладают способностью изменять свою прочность в результате постепенного разрушения жестких структурных связей, обусловливающих структурную прочность грунта Сс. Поэтому длительная прочность скрытопластичных глинистых грунтов рассматривается в зависимости от наличия или отсутствия деформаций ползучести. Если деформации ползучести практически отсутствуют, т. е. τ < τlim, длительная прочность грунта S∞ может быть принята равной полной величине его начальной S0 сдвиговой прочности:
S∞= S0= p∙tgφw+Cc + Σw
Если деформаций ползучести не удается избежать, что обычно наблюдается при τ > τlim, то длительная прочность определится как
S∞= S0= p∙tgφw+ Σw
26. Влияние ползучести на величину показателя консолидации н.Н. Маслова.
В механике грунтов степень влияния ползучести скелета грунта на процесс его консолидации обычно связывается с двумя основными факторами: природной уплотненностью (консистенцией) грунта и степенью его водонасыщения.
Следует отметить, что степень влияния фильтрационных процессов и ползучести скелета грунта на процесс его консолидации (при любой степени водонасыщенности) отчетливо прослеживается по результатам лабораторных испытаний на образцах — близнецах грунта — различной высоты, но в одинаковых условиях их дренирования. Если полученные результаты не зависят от h, делается однозначный вывод, что процесс консолидации целиком определяется ползучестью скелета грунта.
В противном случае проявляется как фильтрационная консолидация, так и ползучесть скелета грунта. Эта особенность была использована (Н.Н.Маслов, 1949 г.) для прогноза времени консолидации грунтовых оснований сооружений. Сущность методики заключается в следующем. Известно, что согласно теории фильтрационной консолидации, когда полностью не учитывается влияние ползучести скелета грунта, имеет место весьма важное соотношение, при котором время уплотнения двух слоев пропорционально квадрату отношения их мощностей:
t2=t1∙[h2/h1]2
где t1 и t2 — время консолидации образцов грунта высотой h1 и h22 соответственно.
В реальном случае, когда на процесс консолидации грунта влияет ползучесть его скелета, это пропорциональность нарушается и формула приобретает иной вид:
t2=t1∙[h2/h1]n
где п — показатель консолидации, принимающий значения в пределах 0< п<2. Если n = 0, то это чистая ползучесть и время консолидации не зависит от мощности слоя грунта. Если n = 2, то это только фильтрационная консолидация.
Определение величины показателя консолидации п выполняется по результатам испытания на консолидацию двух образцов различной высоты. Тогда применительно к одной и той же степени их уплотнения (пористости, влажности) находят t1 и t2, а затем и величину п по формуле
n=[ln(t2/t1)]/ [ln(h2/h1)]
Очень часто этот показатель оказывается близким к n = 1,5.
Применительно к прогнозу консолидации реального слоя грунта мощностью Нсл, уплотнение которого происходит в идентичных условиях дренирования и нагружения (р=const), в соответствии с данной методикой используется формула
Tсл=t[Hсл/h]n
где Tсл и t — соответственно время, требуемое для достижения одной и той же степени уплотнения реального слоя мощностью Hсл и образца грунта высотой h.
Следует заметить, что показатель консолидации n применительно к его использованию для прогноза времени консолидации реальных слоев грунта значительной мощности оказывается достаточно грубой характеристикой и может быть рекомендован лишь для ориентировочных расчетов. Это объясняется зависимостью величины этой характеристики от стадии процесса консолидации и, в частности, от того, что процессы фильтрационной консолидации по-разному проявляются в образцах малой высоты (лабораторный опыт) и слоях грунта значительной мощности.
27. Сопротивляемость сдвигу жестких глин. Формула и график функции Sp=f(p).
жесткие глинистые грунты
К этой группе относятся почти все коренные (до четвертичного возраста) глинистые породы, характеризующиеся, как правило, повышенной прочностью за счет их высокой плотности и цементации. Силы связности Σw за счет процессов старения коллоидов во времени переходят в жесткие структурные связи и оказываются ничтожными по сравнению с силами структурного сцепления Сс. Угол внутреннего трения для коренных пород практически не зависит от влажности.
Выражение сопротивляемости сдвигу жестких глинистых грунтов имеет вид
Sp=p∙tgφ + Cc.
p-норамальное напряжение по площадке сдвига.
Угол внутреннего трения для таких грунтов обычно составляет 17.. .30°, а структурное сцепление Сс - 0,06.. .0,3 МПа (0,6.. .3,0 кгс/см2 ).
Графическая зависимость SP = f(p) для жестких глинистых грунтов имеет вид:

Зависимость сопротивляемости сдвигу жесткой глины от нормальных напряжений
